Посилений закон великих чисел. ЗВЧ Бореля

Посилений закон великих чисел

Нехай є нескінченна послідовність незалежних однаково розподілених випадкових величин 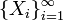, визначених на одному ймовірнісному просторі . Нехай 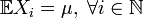. Позначимо 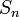вибіркове среднє перших 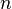членів:

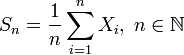Тоді 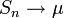майже напевно.

Різниця між слабким і посиленим законами великих чисел

Слабкий закон стверджує, що для великого числа n, середнє значення 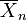правдоподібно є близько до μ . Отже, залишається можливість того, що 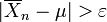трапляється нескінченну кількість разів, хоча й на рідкісних інтервалах.

Посилений закон стверджує що це майже напевно не станеться. Зокрема, це означає що з імовірністю 1, для кожного ε > 0 нерівність 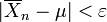виконується для всіх достатньо велеких n. ^[1]

ЗВЧ Бореля

Закон великих чисел Бореля, на честь Еміля Бореля, стверджує, що якщо повторювати експеримент багато раз за тих самих умов і незалежно від інших спроб, то частота певної події наближено дорівнює ймовірності випадання цієї події в кожному окремому експерименті; чим більша кількість повторень тим краще наближення. Точніше, якщо E — подія, pймовірність цієї події і N_n(E) — число разів коли в експерименті випадає подія E в n перших спробах, тоді з ймовірністю 1:

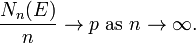
Ця теорема строго формалізує інтуїтивне поняття ймовірності як граничної частоти випадання події в експерименті. Теорема є частковим випадком інших загальніших законів великих чисел в теорії ймовірності.

Центральна гранична теорема — теорема теорії ймовірностей про збіжність розподілу суми незалежних однаковорозподілених випадкових величин до нормального розподілу. Ця теорема підкреслює особливість нормального розподілу в теорії ймовірностей.

Центральна гранична теорема для незалежних послідовностей[ред. • ред. код]

Формулювання Ліндеберга [ред. • ред. код]

Нехай 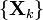— послідовність взаємно незалежних випадкових величин з однаковими розподілами. Припустімо, що та 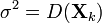існують. Нехай 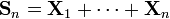. Тоді для довільних фіксованих , ( ):

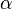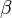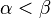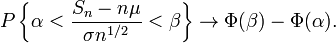
Де — нормальна функція розподілу. ^[1]^[2]

Формулювання Ляпунова [ред. • ред. код]

Теорема названа на честь російського математика Олександра Ляпунова. У цьому варіанті центральної граничної теореми випадкові величини 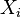мають бути незалежними, але не обов'язково однаково розподіленими. Теорема також вимагає щоб випадкові виличини 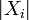мали скінченні моменти деякого порядку (2 + δ ) і швидкість зростання цих моментів має бути обмежена умовою Ляпунова.

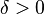ЦГТ Ляпунова ^[3]: Нехай {X_i} — послідовність незалежних випадковех величин, таких, що кожна з них має скінченне математичне сподівання і дисперсію . Позначимо . Якщо для деякого виконується умова Ляпунова

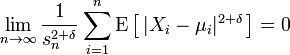
Тоді сума 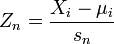прямує за розподілом до стандартного нормального розподілу, при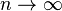

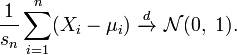
На практиці зазвичай найлегше перевірити умову Ляпунова для 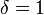. Якщо послідовність випадкових величин задовольняє умову Ляпунова, то вона задовольняє також умову Лінденберга. Зворотне твердження не правильне.

Формулювання Лінденберга [ред. • ред. код]

Докладніше: Умова Лінденберга

Використовуючи ті позначення що й у попередньому параграфі, замінюючи умову Ляпунова на слабшу (запропоновану фінським математиком Ліндебергом у 1920 році) можна отримати нове формулювання центральної граничної теореми.

Якщо для кожного виконуэться

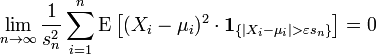
де — характеристична функція. Тоді розподіл стандартизованої суми Z_n прямує до стандартного нормального розподілу N(0, 1).

⇐ Предыдущая 12