
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Слабкий закон великих чисел
Закон великих чисел в теорії імовірностей стверджує, що емпіричне середнє (арифметичне середнє) скінченної вибірки із фіксованого розподілу близьке до теоретичного середнього (математичного сподівання) цього розподілу. В залежності від виду збіжності розрізняють слабкий закон великих чисел, коли має місце збіжність за ймовірністю, і посилений закон великих чисел, коли має місце збіжність майже скрізь.
Завжди знайдеться така кількість випробувань, при якій з будь-якою заданою наперед імовірністю частота появ деякої події буде як завгодно мало відрізнятися від її імовірності.
Форми ЗВЧ
Нижче описано дві версії ЗВЧ: Слабкий закон великих чисел та Посилений закон великих чисел. Обидва закони стверджують, що з певною достовірністю середнє вибірки

прямує до математичного сподівання

де X1, X2, ... — скінченна послідовність н. о. р. випадкові величини зі скінченним математичним сподіванням E(X1) = E(X2) =... = µ < ∞.
Слабкий закон великих чисел
Нехай є нескінченна послідовність однаково розподілених і некорельованих випадкових величин 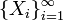 , визначених на одному імовірносному просторі
, визначених на одному імовірносному просторі  . Їх коваріація
. Їх коваріація 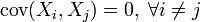 . Нехай
. Нехай 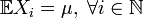 . Позначимо
. Позначимо 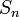 вибіркове середнє перших
вибіркове середнє перших 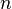 членів:
членів:
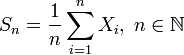 .
.
Тоді 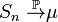 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|