Модуль №10. Кратные интегралы

Модуль №10. Кратные интегралы

Вариант № 7

1. Построить область интегрирования, изменить порядок интегрирования в интеграле: а) dy f(x, y) dx; б) f(x, y) dy.

2. Вычислить 4ye ^2xy dx dy, если D: y = ln 3, y = ln 4, x = 1/2, x = 1.

3. Преобразовать к полярным координатам и вычислить

(x +2)dx dy, если D: x² + y²+ y 0, y x;

4. Найти массу пластинки D, если плотность 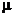=12x y²,

D: x²+ y²= 9, x , y 0.

5. Найти координаты центра тяжести однородной фигуры, ограниченной линиями x = 0, y = 0, 2x + 3y = 6.

6. Вычислить x dx dy dz, если V – пирамида, ограниченная координатными плоскостями и плоскостью x + y + z = 3.

7. Преобразовать к цилиндрическим координатам и вычислить

dx dy (z - 2 ) dz.

8. Преобразовать к сферическим координатам и вычислить:

dx dy dz, если V: x²+ y²+ z²- 2z = 0.

9. Найти объём тела, ограниченного поверхностями:

z = 0, x = 0, y = 0, x²= z + 4, 3x + 2y = 6.

10. Найти массу тела плотностью 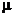= z, ограниченного поверхностями:

x² + y² + z² = 3, x² + y² 2, z = 0.