Предел функции. 1. Предел функции в точке. 2. Предел функции на бесконечности. 3. Односторонние пределы. 4. Бесконечно малые и бесконечно большие функции (б.м.ф. и б.б.ф.)

Предел функции

Справочный материал

1. Предел функции в точке

Определение (на «языке последовательностей» или по Гейне ). Число А наз. пределом функции y = f(x) в точке х₀

(при х→ х₀), если для любой последовательности допустимых значений аргумента {х_n}, nÎ N, (x_n ≠ x₀), сходящейся к x₀,

последовательность соответствующих значений функции {f(x_n)}, nÎ N сходятся к числу А.

Запись: 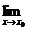f(x) = А или f(x) → А при х→ х₀.

Определение (на «языке e-d» или по Коши)

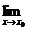f(x) = А Û .

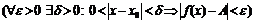2. Предел функции на бесконечности

А = 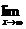f(x) Û .

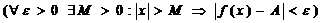Различают f(x) и f(x).

3. Односторонние пределы

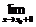f(x) = А₁– правый предел функции (при х→ х₀справа) Û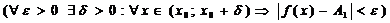

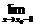f(x) = А₂– левый предел функции (при х→ х₀слева) Û .

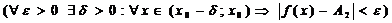4. Бесконечно малые и бесконечно большие функции (б. м. ф. и б. б. ф. )

Функция a(x) - б. м. ф. при х→ х₀, если 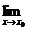f(x) = 0 или f(x) → 0 при х→ х_0.

Свойства б. м. ф.

1⁰ Алгебраическая сумма конечного числа б. м. ф. в точке х₀ есть б. м. ф.

2⁰ Произведение ограниченной функции на б. м. есть б. м. ф.

3⁰ Произведение конечного числа б. м. ф. есть б. м. ф.

4⁰ Произведение постоянной на б. м. есть б. м.

Теорема (о связи функции, ее предела и б. м. ). 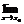f(x) = А Û f(x) = А + a(x), где a(x) - б. м. ф. в точке х₀.

Функция f(x)-б. б. ф. при х→ х₀, т. е. 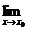f(x) = ¥ Û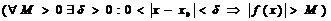

Функция f(x)-б. б. ф. при х→ ¥, т. е. 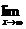f(x) = ¥ Û .

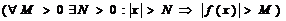f(x) → + ¥ - положительная б. б. ф., f(x) → -¥ - отрицательная б. б. ф.

Теорема (о связи б. м. ф. и б. б. ф. ). Функция a(x) - б. м. при х→ х₀(х→ ¥ ) Û 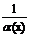- б. б. ф. при х→ х₀(х→ ¥ ) и, наоборот.

5. Теоремы о пределах. Если 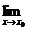f(x) = А, 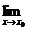g(x) = B, то

1. 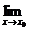(f(x) g(x)) = А 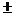B Следствие 1. 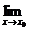с = с, 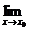x = x₀

2. 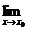(f(x) × g(x)) = А × B 2. 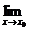(с× f(x)) = с× 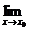f(x)

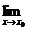
3. 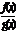= 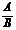, (В ¹ 0, g(x) ¹ 0). 3. 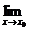(f(x))ⁿ= ( 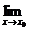f(x))ⁿ.