Сущность математических понятий (множество, виды множеств, операции над множествами).

Сущность математических понятий (множество, виды множеств, операции над множествами).

Первое понятие Множество.

Ввел понятие множества немецкий ученый Г. Кантор в XIX веке, основоположник теории множеств.

Множество есть нечто мыслимое нами, как единое.

Г. Кантор

Дети воспринимают множества, которые окружают их с раннего детства (множество игр, множество деревьев, множество домов и т. д. ).

Интересный пример множества в стихах Асадова

В любых делах, примаксимуме сложностей,

Подход к проблеме все-таки один.

Желанье - это множество возможностей,

А нежеланье — это множество причин.

Виды множеств

Множества могут быть разной природы. Природа множеств определяется элементами, его составляющими. Например: множество звуков, движений, предметов, явлений, ощущений и т. д.

По количеству элементов, входящих в множество, множество делится на конечные, бесконечные и пустые.

Конечные множества — это множества, элементы которых можно исчерпать забирая по одному.

Например: дни недели, стулья в классе, мячи в корзине и т. д. численность конечных множеств можно выразить натуральным числом. Например: в неделе - 7 дней, стульев - 30 и т. д.

Бесконечные множества - это множества, элементы которых нельзя исчерпать забирая по одному.

Например: множество звезд, натуральных чисел и т. д.

Пустые множества ~ это множества, не содержащее ни одного элемента.

Например: из корзины забираю все грибочки - в корзине ничего не осталось, т. е. множество стало пустым.

Способы задания множеств

1. Множество можно задать перечислением (треугольники, кружочки, квадратики и т. д. ).

2. Задание характеристического свойства множества, т. е. свойства, которым владеют все элементы данного множества (геометрические фигуры).

3. Схематическо-графический (1, 2, 3; палочки Кьюзенера)

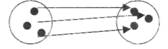Эквивалентные множества — это множества между элементами которых можно установить взаимно-однозначные соответствия.

12 Следующая ⇒