3. Относительная частота и вероятность. Аксиоматика Колмогорова

1. Этапы возникновения и развития современной теории вероятности.

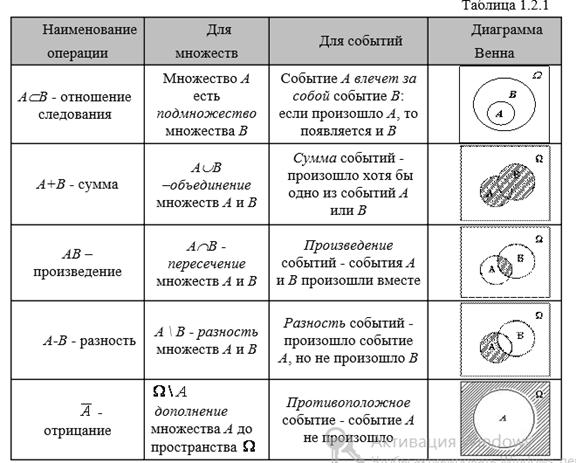
2. Пространство элементарных исходов. Случайные события и операции с ними.

Теория вероятностей изучает случайные явления не непосредственно, а с помощью идеализированных математических моделей случайных опытов.

Всякий случайный опыт (испытание, эксперимент) состоит в осуществлении некоторого комплекса условий и наблюдении результата. Любой наблюдаемый результат опыта интерпретируется как случайный исход (случайное событие). Случайное событие в результате опыта может произойти, а может и не произойти.

Каждому опыту ставится в соответствие пространство элементарных исходов . Это множество простейших (т. е. неразложимых в рамках данного опыта на более простые) взаимоисключающих исходов, таких, что результатом эксперимента всегда является один и только один исход

3. Относительная частота и вероятность. Аксиоматика Колмогорова

Относительная частота наряду с вероятностью принадлежит к основным понятиям теории вероятностей.

Относительной частотой события называют отношение числа испытаний, в которых событие появилось, к общему числу фактически произведенных испытаний. Таким образом, относительная частота события А определяется формулой

W (А) = m / n,

где m - число появлений события, n - общее число испытаний.

Сопоставляя определения вероятности и относительной частоты, заключаем: определение вероятности не требует, чтобы испытания производились в действительности; определение же относительной частоты предполагает, что испытания были произведены фактически. Другими словами, вероятность вычисляют до опыта, а относительную частоту - после опыта.

12 Следующая ⇒