Необходимые и достаточные условия.

Необходимые и достаточные условия.

Необходимым условием правильности утверждения называется такое условие, без соблюдения которого утверждение заведомо не может быть верным.

Фраза «для 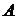необходимо 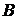» тождественна любой из приведенных ниже:

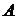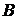– если , то (из 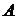следует 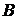). – если «не 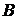», то «не 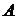» (из отсутствия 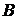следует отсутствие ).

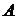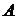– выполнено только тогда, когда выполнено 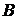( 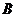может выполняться и при отсутствии )

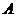Пример 1:

Для того, чтобы треугольник был равносторонним, необходимо, чтобы он был равнобедренным.

Тождественные формулировки:

– если треугольник равносторонний, то он равнобедренный

– если треугольник не равнобедренный, то он не равносторонний.

Пример 2:

Для того, чтобы ряд 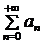сходился, необходимо, чтобы .

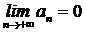Тождественные формулировки:

– если ряд 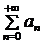сходится, то 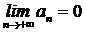. – если 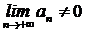, то. ряд 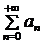расходится.

Достаточным условием правильности утверждения называется такое условие, при котором утверждение заведомо верно.

Фраза «для 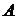достаточно 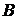» тождественна любой из приведенных ниже:

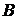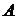– если , то (из 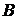следует ).

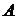– если «не 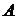», то «не 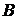» (из отсутствия 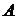следует отсутствие ).

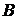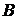– выполнено только тогда, когда выполнено 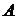( 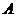может выполняться и при отсутствии )

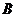Пример 1:

Для того, чтобы треугольник был равнобедренным, достаточно, чтобы он был равносторонним.

Тождественные формулировки:

– если треугольник равносторонний, то он равнобедренный

– если треугольник не равнобедренный, то он не равносторонний.

Пример 2:

Для того, чтобы ряд 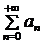расходился, достаточно, чтобы .

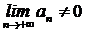Тождественные формулировки:

– если 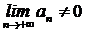, то, ряд 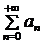расходится. – если ряд 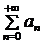сходится, то .

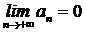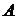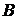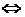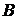Замечание: «для необходимо » «для достаточно ».

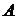Пример:

Для того, чтобы четырёхугольник был ромбом, достаточно, чтобы он был квадратом. Для того, чтобы четырёхугольник был квадратом, необходимо, чтобы он был ромбом.

12 Следующая ⇒