Док-во: по индукции при n=1 верно утверждение

⇐ ПредыдущаяСтр 2 из 2

Док-во: по индукции при n=1 верно утверждение

2) Считаем правельней формулу n=n-1

3) Разложим определитель n-ого порядка det A по элементам первой строки

Разложим det A по элементам первой строки, а det A¹ по элементам первого столбца

II. -При перестановки двух строк определитель меняет знак, тоже по индукции

-Раскладывем элементы по элементам-не переставляемой строки.

III. Определитель с двумя равными строками равен нулю

IV. Определитель с нулевой трокой равн нулю

V. При умножении строки на число, ∆ умножается на это число.

СЛАУ-называется система уравнений вида:

a11 x1+a12 x2+.. +a1n xn=b1

a21 x1+a22 x2+.. +a2n xn=b2 }

am1 x1+am2 x2+.. +amn xn=bm

Решением СЛАУ называется совокупность значений x1, x2.. xn подстановка которых в СЛАУ превращает все уравнение в тождество. Если b=0 то слау называется одномерной.

Матричная запись

СЛАУ можно записывать виде AX=B

Решение СЛАУ, метод Гаусса. С помощью метода Гаусса нужно работать со строками. Приводим расширенную матрицу к треугольному виду.

Теорема Кропенера-Капелли: СЛАУ совместно тогда и только тогда когда Rg A=Rg A* Теорема Гаусса: приводим матрицу к треугольному виду, получаем нули под а11 который не равен нулю, и под а22 и т. д., затем и получаем треугольный вид.

Вектором называется направленный отрезок прямой, обозначающийся:

Ветор а, ветор b, вектор AB. Бывают на плоскости или в трехмерном пространстве.

-коллиниальные векторы аІІb, это векторы лежащие на параллельных прямых.

-Компланарные –векторы лежащие на параллельных плоскостях.

Умножение векторов на число: la¯ l=ά lb¯ l, a¯ ll¯ b, при ά > 0-сонаправ., при ά < 0-против. направ.,

ά =0- колин.

Корд. Векторов-координаты вектора в данном базисе.

Скаляр произв. (a¯, c¯ )=la¯ l*llc¯ l*cosφ

Свойства: 1) (a¯, b¯ )=(b¯, a¯ ). 2) (λ a¯ μ b¯ )=λ μ (a¯, b¯ ). 3) (a¯ +b¯ +c¯ )=(a¯, c¯ )+(b¯, c¯ )

Векторыные произв. 1) [a¯, b¯ ]=c¯, lc¯ l=la¯ llb¯ l*sinφ

2) c¯ ‗ І‗ a и c¯ ‗ І‗ b¯. 3) a¯, b¯, c¯ -правая тройка

Минор 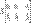матрицы A ― определитель квадратной матрицы порядка k (который называется также порядком этого минора), элементы которой стоят в матрице A на пересечении строк с номерами 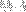и столбцов с номерами .

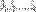Базисным минором матрицы называется любой её ненулевой минор максимального порядка.

Общее уравнение прямой:

{ a1 x+ b1y+c1z+ d1=0

a2 x+ b2y+c2z+ d2=0

Каноническое уравнение прямой:

x-x0=y-y0=z-z0

m n p (дробь)

Гипербола -кривая, описываемая каноничным уравнением x² -y²

_ _=1

a² b²

Гиперболой называют геометрическое место точек, разность расстояний, которые и есть фокус расстояния.

Парабола -кривая описываемая уравнением: x² =(x² =-2py,

y² =2px,

y² =-2px)

Парабола-геометрическое место точек, расстояние которых от фокуса и директрисы равны.

Оптика -если в фокус эллипса поместить точечный источник света, то отражение от параболы лучи пойдут в доль оси x.

Элипсис -геометрическое место точек, сумма расстояний которых до двух данных точек, называемых фокусами, есть постоянная величина 2а, большая, чем расстояние между фокусами 2с.

Построение общего решения методом Гаусса:

1) Проверить, имеется ли в системе протеворечивое уравнение. Если такое уравнение в системе есть, то она несовместна и не имеет общего решения.

2) Вычеркнуть все тривиальные уравнения в системе если они есть

3) Выяснить является ли система уравнений разрешенной. Если разрешенная. то построить общее решение, выражая разрешенные не известные через свободные.

4) Найти уравнение в системе не содержащее разрешенного неизвестного. С помощью элементарных преобразований получить в этом уравнении неизвестное с коэффициентом единица, а затем исключить это неизвестное из остальных уравнений системы.

5) Перейти к выполнению пунката 1. Через конечное число шагов процесс остановится и будет установлена несовместность системы или получено общее решение системы линейных уравнений.

Два вектора называются ортогональными если их скалярное произведение равно нулю. Система векторов называется ортоганальной, если векторы этйо системы попарно ортогональны, ортогональная система нулевых веторок линейно независима.

СЛАУ совместно тогда и только тогда, когда ранги систем векторов совпадают Rg A= Rg A*

⇐ Предыдущая 12