Реальный газ

1. Реальный газ — газ, который не описывается уравнением состояния идеального газа Клапейрона — Менделеева.

Зависимости между его параметрами показывают, что молекулы в реальном газе взаимодействуют между собой и занимают определенный объем. Состояние реального газа часто на практике описывается обобщенным уравнением Менделеева — Клапейрона:

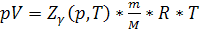где p — давление; T — температура; Zr = Zr (p, T) — коэффициент сжимаемости газа; m - масса; М — молярная масса; R — газовая постоянная.

2. Межмолекулярное взаимодействие имеет электрическую природу и складывается из сил притяжения (ориентационных, индукционных и дисперсионных) и сил отталкивания.

Межмолекулярное взаимодействие — это взаимодействие между электрически нейтральными молекулами или атомами.

Межмолекулярные взаимодействия, взаимодействие молекул между собой, не приводящее к разрыву или образованию новых химических связей. Межмолекулярные взаимодействия определяют отличие реальных газов от идеальных, существование жидкостей и молекул кристаллов. От Межмолеку- лярных взаимодействий зависят многие структурные, спектральные, термодинамическое, теплофизических и другие свойства веществ. Появление понятия " межмолекулярные взаимодействия" связано с именем Й. Д. Ван-дер-Ваальса, который для объяснения свойств реальных газов и жидкостей предложил в 1873 уравение состояния, учитывающее межмолекулярные взаимодействия, поэтому силы межмолекулярных взаимодействий часто называют ван-дер-ваальсовыми.

Виды межмолекулярных взаимодействий. Основу межмолекулярных взаимодействий составляют кулоновские силы взаимодействие между электронами и ядрами одной молекулы и ядрами и электронами другой. В экспериментально определяемых свойствах вещества проявляется усредненное взаимодействие, которое зависит от расстояния R между молекулами, их взаимной ориентации, строения и физических характеристик (ди-польного момента, поляризуемости и др. ). При больших R, значительно превосходящих линейные размеры 1 самих молекул, вследствие чего электронные оболочки молекул не перекрываются, силы межмолекулярных взаимодействий можно достаточно обоснованно подразделить на три вида - электростатические, поляризационные (индукционные) и дисперсионные. Электростатические силы иногда называют ориентационными, однако это неточно, поскольку взаимная ориентация молекул может обусловливаться также и поляризационными силами, если молекулы анизотропны.

При малых расстояниях между молекулами (R ~ l) различать отдельные виды межмолекулярных взаимодействий можно лишь приближенно, при этом, помимо названных трех видов, выделяют еще два, связанные с перекрыванием электронных оболочек, - обменное взаимодействие и взаимодействия, обязанные переносу электронного заряда. Несмотря на некоторую условность, такое деление в каждом конкретном случае позволяет объяснять природу межмолекулярных взаимодействий и рассчитать его энергию.

Энергия электростатическоговзаимодействия Vэл-ст представляет собой энергию кулоновского взаимодействия, вычисленную в предположении, что распределение зарядовой плотности отвечает изолированным молекулам (R =∞ ). В общем случае электрический потенциал вокруг молекулы изменяется не только по абсолютной величине, но и по знаку. Если взаимная ориентация двух молекул такова, что область положительного потенциала одной из них приблизительно совпадает с областью, в которой локализован отрицательный заряд другой, то Vэл-ст < 0, т. е. электростатичное взаимодействие молекул ведет к их притяжению. При R> > 1энергия Vэл-ст становится равной сумме энергий взаимодействий мультиполей (диполей, квадруполей и т. д. ); для полярных молекул главный вклад дает обычно диполь-дипольное взаимодействие. Его энергия Vдип-дип может иметь разный знак в зависимости от ориентации диполей. При ориентации молекул А и В, соответствующей минимуму энергии взаимодействие, Vдип-дип = — 2pApB/R3, где pА и рB - дипольные моменты молекул А и В соответственно. В газовой фазе, где молекулы почти свободно вращаются, более вероятны такие их взаимные ориентации, которые отвечают притяжению диполей. [1]-Химическая энциклопедия. И. Л. Кнунянц, том 3, с. 150

3. Предпринималось много попыток для учета отклонений свойств реальных газов от свойств идеального газа путем введения различных поправок в уравнение состояния идеального газа. Наибольшее распространение вследствие простоты и физической наглядности получило уравнение Ван-дер-Ваальса (1873).

Первая поправка в уравнении состояния идеального газа рассматривает собственный объем, занимаемый молекулами реального газа. В уравнении Дюпре (1864):

p (V – nb) = nRT

постоянная b учитывает собственный мольный объем молекул.

При понижении температуры межмолекулярное взаимодействие в реальных газах приводит к конденсации (образование жидкости). Межмолекулярное притяжение эквивалентно существованию в газе некоторого внутреннего давления π (иногда его называют статическим давлением). Изначально величина π была учтена в общей форме в уравнении Гирна (1865):

(p + π ) (V – nb) = nRT

Ван-дер-Ваальс в 1873 г. дал функциональную интерпретацию внутреннего давления. Согласно модели Ван-дер-Ваальса, силы притяжения между молекулами (силы Ван-дер-Ваальса) обратно пропорциональны шестой степени расстояния между ними, или второй степени объема, занимаемого газом. Считается также, что силы притяжения суммируются с внешним давлением. С учетом этих соображений уравнение состояния идеального газа преобразуется в уравнение Ван-дер-Ваальса:

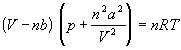(1)

или для одного моля

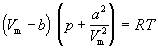(2)

Второе уравнение можно переписать так, чтобы выразить в явном виде давление

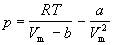
или объем:

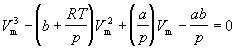
Принципиальное значение уравнения Ван-дер-Ваальса определяется следующими обстоятельствами:

1) уравнение было получено из модельных представлений о свойствах реальных газов и жидкостей, а не явилось результатом эмпирического подбора функции f(p, V, T), описывающей свойства реальных газов;

2) уравнение долго рассматривалось как некоторый общий вид уравнения состояния реальных газов, на основе которого было построено много других уравнений состояния;

3) с помощью уравнения Ван-дер-Ваальса впервые удалось описать явление перехода газа в жидкость и проанализировать критические явления. В этом отношении уравнение Ван-дер-Ваальса имеет преимущество даже перед более точными уравнениями в вириальной форме.

Причиной недостаточной точности уравнения Ван-дер-Ваальс считал ассоциацию молекул в газовой фазе, которую не удается описать, учитывая зависимость параметров a и b от объема и температуры, без использования дополнительных постоянных. После 1873 г. сам Ван-дер-Ваальс предложил еще шесть вариантов своего уравнения, последнее из которых относится к 1911 г. и содержит пять эмпирических постоянных. Две модификации уравнения (1) предложил Клаузиус, и обе они связаны с усложнением вида постоянной b. Больцман получил три уравнения этого типа, изменяя выражения для постоянной a. Всего известно более сотни подобных уравнений, отличающихся числом эмпирических постоянных, степенью точности и областью применимости. Выяснилось, что ни одно из уравнений состояния, содержащих менее 5 индивидуальных постоянных, не оказалось достаточно точным для описания реальных газов в широком диапазоне p, V, T, и все эти уравнения оказались непригодными в области конденсации газов.

4. Уравнение Клапейрона-Менделеева достаточно хорошо описывает газ при высоких температурах и низких давлениях, когда он находится в условиях достаточно далёких от условий конденсации. Однако для реального газа это не всегда выполняется и тогда приходится учитывать потенциальную энергию взаимодействия молекул газа между собой. Простейшим уравнением состояния, описывающим неидеальный газ, является уравнение, предложенное в 1873 г. Иоханнесом Дидериком Ван-дер-Ваальсом (1837 - 1923)

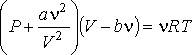(1)

где: , и 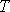- давление, объём и температура газа, -количество молей газа, и 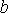- постоянные для данного газа. Для различных газов постоянные и 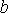различны, и их можно определить экспериментально. Значение константы 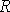такое же, как и для идеального газа. Такой вид уравнения состояния реального газа имеет как экспериментальные, так и молекулярно-кинетические обоснования. Остановимся сначала на последних.

Пусть на молекулы газа действуют силы притяжения и отталкивания. И те, и другие силы действуют на небольших расстояниях, но силы притяжения убывают медленнее сил отталкивания. Силы притяжения относятся к взаимодействию молекулы с её ближайшим окружением, а сила отталкивания - проявляется в момент столкновения двух молекул.

Силы притяжения внутри газа в среднем скомпенсированы для каждой отдельной молекулы. На молекулы, расположенные в тонком слое вблизи стенки сосуда, действует сила притяжения со стороны других молекул, направленная внутрь газа, которая создает давление, добавочное к создаваемому самой стенкой. Это давление иногда называют внутренним давлением.

Суммарная сила внутреннего давления, действующая на элемент поверхностного слоя газа должна быть пропорциональна числу молекул газа в этом элементе и также числу молекул в слое газа, непосредственно примыкающему к рассматриваемому элементу поверхностного слоя. Толщина этих слоёв определяется радиусом действия сил притяжения и имеет тот же порядок величины. При увеличении концентрации молекул газа в раз, сила притяжения, приходящаяся на единицу площади приповерхностного слоя, возрастёт в 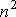раз. Поэтому величина внутреннего давления растёт пропорционально квадрату концентрации молекул газа. Тогда для суммарного давления внутри газа 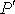можно записать:

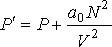(2)

где: - давление газа, которое действует на стенку сосуда (по третьему закону Ньютона стенка действует на газ с тем же давлением), 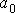- постоянная, определяемая физико-химическими характеристиками молекул газа, 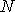- число молекул газа в объеме . Отношение 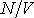представляет собой концентрацию молекул газа. Величина - это давление, которое создавал бы идеальный газ при тех же условиях.

Вводя обозначение:

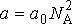(3)

где: 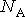- постоянная Авогадро, имеем

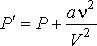(4)

Итак, нами получен вид поправки к давлению, которая необходима для того, чтобы учесть слабые силы притяжения в реальном газе, отличающие его от идеального. При этом в формуле для нахождения суммарного давления внутри газа появилась новая постоянная , зависящая от свойств газа.

Рассмотрим теперь поправку, связанную с действием сил отталкивания. Поскольку нами будут учитываться только парные взаимодействия между молекулами, то эта сила, в отличие от силы притяжения, не будет зависеть от концентрации молекул. По этой же причине сила отталкивания проявляется во всём объёме газа, а не только в приповерхностном слое. Зависимость этой силы от расстояния между молекулами определяет эффективное сечение взаимодействия молекул, то есть, по сути, их размеры.

Таким образом, в случае проявления короткодействующих сил отталкивания, невозможно аппроксимировать молекулы материальными точками и пренебречь их размерами. Поэтому необходимо ввести поправку, учитывающую объём, занимаемый молекулами. Её величина будет пропорциональна общему числу молекул 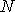, а также зависеть от их физико-химических свойств. Тогда свободный от молекул объем 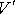можно определить следующим образом:

(5)

где: 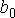- коэффициент, определяемый свойствами молекул. Вводя обозначение:

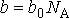(6)

представим формулу (5) в виде:

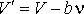(7)

Величину 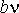и, таким образом, величину эффективного объёма, занимаемого молекулами, нельзя получить из простых механических моделей, так как сами размеры молекул определяются характером сил отталкивания. Поскольку уравнение Ван-дер-Ваальса является по сути своей эмпирическим, коэффициент 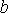, так же как и коэффициент , должны определяться в первую очередь экспериментально.

Если теперь в левой части уравнения Клапейрона-Менделеева:

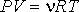
произвести замену произведения 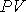на произведение

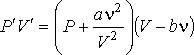
то получится уравнение Ван-дер-Ваальса.

Введение поправки, обусловленной действием сил притяжения, привело к тому, что уравнение состояния стало кубическим относительно объёма, а число постоянных, являющихся его параметрами, стало равным трем. Как известно, кубическое уравнение имеет три корня. Для уравнения Ван-дер-Ваальса имеют место два следующих случая: а) корни действительны; б) два корня мнимые и один корень действительный.

12 Следующая ⇒