- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
НЕРАВНОВЕСНЫЕ СОСТОЯНИЯ
3. Длина свободного пробега и число столкновений молекул
3. 1. Найти среднюю длину свободного пробега молекул водорода при давлении р=0, 1 Па и температуре Т=100К.
6, 4 см
3. 2. При помощи манометра, установленного на искусственном спутнике Земли, было обнаружено, что на высоте 300 км от поверхности Земли в 1 см3 атмосферы находится около миллиарда частиц газа. Найти среднюю длину свободного пробега частиц на этой высоте. Диаметр частиц принять равным 0, 2 нм.
5, 6 км
3. 3. Найти среднюю длину свободного пробега молекул воздуха при нормальных условиях. Диаметр молекул воздуха принять равным 0, 3 нм.
93 нм
3. 4. Баллон вместимостью 10 л содержит водород массой 1 г. Определить среднюю длину свободного пробега молекул.
1, 55 нм
3. 5. Найти среднюю длину свободного пробега атомов гелия в условиях, когда плотность гелия 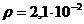 кг/м3.
кг/м3.
1, 8 мкм
3. 6. Функция распределения молекул по длинам свободного пробега х имеет вид f(х)=Ае-kх. Определить относительное число молекул, длина свободного пробега которых: а) меньше 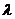 ; б) заключена в диапазоне от
; б) заключена в диапазоне от 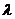 до 2
до 2 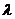 , где
, где 
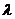 - длина свободного пробега.
- длина свободного пробега.
0, 63; 0, 23
3. 7. Найти среднее число столкновений, испытываемых в течение 1 с молекулой кислорода при нормальных условиях.

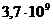 с-1
с-1
3. 8. Найти число N всех соударений, которые происходят в течение 1 с между всеми молекулами водорода, занимающего при нормальных условиях объем 1 мм3.

3. 9. Найти зависимость средней длины свободного пробега молекул газа от давления при следующих условиях: а) изохорическом; б) изотермическом.
Не зависит
~1/р
3. 10. Какое предельное число молекул газа должно находиться в 1 см3 сферического сосуда, чтобы молекулы не сталкивались друг с другом? Диаметр молекулы газа принять равным 0, 3 нм.
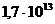 см-3
см-3
4. Явления переноса: диффузия, вязкость, теплопроводность.
4. 1. Средняя длина свободного пробега атомов гелия при нормальных условиях равна 180 нм. Определить диффузию D гелия.
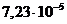 м2/с
м2/с
4. 2. Вычислить диффузию D азота: а) при нормальных условиях; б) при давлении 100 Па и температуре 300К.

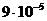 м2/с
м2/с
0, 061 м2/с
4. 3. Определить зависимость диффузии D от температуры Т при следующих процессах: а) изобарическом; б) изохорическом.
~ 
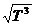

4. 4. Определить зависимость коэффициента диффузии D от давления р при следующих процессах: а) изотермическом; б) изохорическом.

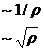
4. 5. Найти массу азота, прошедшего вследствие диффузии через площадку 100 см2 за 10 с, если градиент плотности в направлении, перпендикулярном площадке, равен 1, 26 кг/м4. Температура азота равна 270С; средняя длина свободного пробега молекул азота 10 мкм.

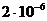 кг
кг
4. 6. Вычислить динамическую вязкость кислорода при нормальных условиях.
18 мкПа с
4. 7. Найти среднюю длину свободного пробега молекул азота при условии, что его динамическая вязкость 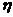 =17мкПа с.
=17мкПа с.
90 пм
4. 8. Определить зависимость динамической вязкости от температуры при следующих процессах: а) изобарическом; б) изохорическом.
4. 9. Определить зависимость динамической вязкости от давления при следующих процессах: а) изотермическом; б) изохорическом.
4. 10. Найти коэффициент внутреннего трения азота при нормальных условиях, если коэффициент диффузии для него при этих условиях равен 0, 142 см2/с.
17, 8 мкПа с
4. 11. Найти диаметр молекулы кислорода, если известно, что для кислорода коэффициент внутреннего терния при 00С равен 18, 8 мкПа с.
0, 3 нм
4. 12. Найти коэффициент диффузии и внутреннего трения воздуха при давлении 760 мм рт. ст. и температуре 100С. Диаметр молекулы воздуха принять равным 0, 3 нм.
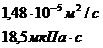
4. 13. Коэффициент диффузии и внутреннего трения кислорода равны соответственно D= 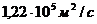 и
и 
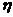 =19, 5 мкПа с. Найти при этих условиях: а) плотность кислорода; б) среднюю длину свободного пробега его молекул; в) среднюю арифметическую скорость его молекул.
=19, 5 мкПа с. Найти при этих условиях: а) плотность кислорода; б) среднюю длину свободного пробега его молекул; в) среднюю арифметическую скорость его молекул.
1, 6 кг/м3
83, 5 нм
440 м/с
4. 14. Цилиндр радиусом R1=10 см и длиной L=30 см расположен внутри цилиндра радиусом R2=10, 5 см так, что оси обоих цилиндров совпадают. Малый цилиндр неподвижен, большой вращается относительно геометрической оси с частотой n =15 с-1. Динамическая вязкость газа, в котором находятся цилиндры, равна 
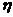 =8, 5 мкПа с. Определить: а) касательную силу
=8, 5 мкПа с. Определить: а) касательную силу 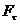 , действующую на поверхность внутреннего цилиндра площадью S== 1 м2; б) вращающий момент М, действующий на этот цилиндр.
, действующую на поверхность внутреннего цилиндра площадью S== 1 м2; б) вращающий момент М, действующий на этот цилиндр.
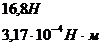
4. 15. Два горизонтальных диска радиусами R=20 см расположены друг над другом так, что оси их совпадают. Расстояние d между плоскостями дисков равно 0, 5 см. Верхний диск неподвижен, нижний вращается относительно геометрической оси с частотой n=10 с-1. Найти вращающий момент М, действующий на верхний диск. Динамическая вязкость воздуха между дисками 17, 2 мкПа с.
0, 58 мН м
4. 16. Горизонтально расположенный диск радиусом R=0, 2 м подвешен на тонкой упругой нити над таким же укрепленным на вертикальной оси диском. Коэффициент кручения нити (отношение приложенного вращающего момента к углу закручивания) 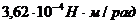 . Зазор между дисками 5 мм. На какой угол закручивается нить, если нижний диск привести во вращение с угловой скоростью
. Зазор между дисками 5 мм. На какой угол закручивается нить, если нижний диск привести во вращение с угловой скоростью 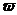 =20 рад/c?
=20 рад/c?
0, 48 рад
4. 17. Найти зависимость теплопроводности от температуры Т при следующих процессах: а) изобарическом; б) изохорическом.
4. 18. Найти зависимость теплопроводности от давления р при следующих процессах: а) изотермическом: б) изохорическом.
4. 19. Пространство между двумя большими параллельными пластинами, расстояние между которыми равно 5 мм, заполнено гелием. Температура Т1 одной пластины поддерживается 290К, другой – Т2=310К. Вычислить плотность теплового потока для двух случаев: а) р=0, 1 МПа; б) р=1 МПа.
196 Вт/м2
35 мВт/м2
4. 20. Зазор между двумя очень длинными коаксиальными цилиндрическими поверхностями заполнен однородным изотропным веществом. Радиусы поверхностей r1=5 см, r2=7 см. Внутренняя поверхность поддерживается при температуре Т1=290К, наружная поверхность – при Т2=320К. Найти для средней части цилиндров зависимость температуры Т от расстояния r до оси.

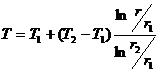
4. 21. Между двумя пластинами, находящимися на расстоянии 1 мм друг от друга, находится воздух. Между пластинами поддерживается разность температур 
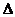 Т=1К. Площадь каждой пластины равна S=100 см2. Какое количество теплоты передается за счет теплопроводности от одной пластины к другой за 10 мин? Считать, что воздух находится при нормальных условиях. Диаметр молекулы воздуха принять равным 0, 3 нм.
Т=1К. Площадь каждой пластины равна S=100 см2. Какое количество теплоты передается за счет теплопроводности от одной пластины к другой за 10 мин? Считать, что воздух находится при нормальных условиях. Диаметр молекулы воздуха принять равным 0, 3 нм.
78 Дж
II. РЕАЛЬНЫЕ ГАЗЫ И ЖИДКОСТИ
5. Уравнение Ван-дер-ваальса
5. 1. В баллоне вместимостью V=8 л находится кислород массой m=0, 3 кг при температуре Т ==300К. Найти, какую часть вместимости сосуда составляет собственный объем молекул газа. Определить отношение внутреннего давления 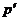 к давлению р газа на стенки сосуда.
к давлению р газа на стенки сосуда.
0, 91%
6, 3%
5. 2. В сосуде вместимостью V=10 л находится азот массой m=0, 25 кг. Определить: а) внутреннее давление 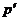 ; б) собственный объем
; б) собственный объем 
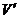 молекул.
молекул.
108 кПа
86, 2 см3
5. 3. В сосуде вместимостью V=0, 3 л находится углекислый газ, содержащий 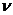 =1 моль при температуре Т=300К. Определить: а) давление газа по уравнению Менделеева-Клапейрона; б) по уравнению Ван-дер-Ваальса.
=1 моль при температуре Т=300К. Определить: а) давление газа по уравнению Менделеева-Клапейрона; б) по уравнению Ван-дер-Ваальса.
8, 31 Мпа
5, 67 Мпа
5. 4. Определить наибольший объем Vmax, который может занимать вода, содержащая количество вещества 1 моль. 
91, 2 см3
5. 5. Определить плотность водяных паров в критическом состоянии.
197 кг/м3
5. 6. Во сколько раз концентрация nкр молекул азота в критическом состоянии больше концентрации n0 молекул при нормальных условиях?
В 193 раза
5. 7. Найти среднюю длину свободного пробега молекул углекислого газа при нормальных условиях. Эффективный диаметр молекулы вычислить, считая известными для углекислого газа критические температуру и давление.
79 нм
5. 8. Найти внутреннюю энергию U углекислого газа массой m=132 г при нормальном давлении р0 и температуре Т=300К в двух случаях, когда газ рассматривают: а) как нормальный; б) как реальный.
22, 4 кДж
9, 2 кДж
5. 9. Определить изменение внутренней энергии неона, содержащего 1 моль, при изотермическом расширении его объема от 1 л до 2 л.
104 Дж
5. 10. В сосуде вместимостью 1 л содержится 10 г азота, определить изменение температуры азота, если он расширяется в пустоту до объема 10 л.
–20, 9К
5. 11. Газообразный хлор массой 7, 1 г находится в сосуде вместимостью 0, 1 л. Какое количество теплоты Q необходимо подвести к хлору, чтобы при расширении его в пустоту до объема 1 л температура газа осталась неизменной?
58, 5 Дж
5. 12. Определить для газа Ван-дерВаальса разность молярных теплоемкостей ср – сv. Вычислить эту разность для азота в объеме 1 л при температуре -1000 выразить ее через R).
1, 21 R
6. Поверхностное натяжение. Капиллярные явления.
6. 1. Какую силу нужно приложить к горизонтальной алюминиевой шайбе толщиной h=10 мм, внутренним диаметром d1=50 мм и внешним диаметром d2=52 мм, чтобы оторвать ее от поверхности воды? Какую часть от найденной силы составляют силы поверхностного натяжения?
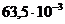 Н
Н
37%
6. 2. Кольцо внутренним диаметром 25 мм и внешним диаметром 26 мм подвешено на пружине с коэффициентом упругости 10-4 кгс/мм и соприкасается с поверхностью жидкости. При опускании поверхности жидкости кольцо оторвалось от нее при растяжении пружины на 5, 3 см. Найти коэффициент поверхностного натяжения жидкости.

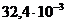 Н/м
Н/м
6. 3. Масса 10 капель спирта, вытекающего из капилляра, равна 0, 71 г. Определить поверхностное натяжение 
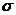 спирта, если диаметр d шейки капли в момент отрыва равен 1 мм.
спирта, если диаметр d шейки капли в момент отрыва равен 1 мм.
22, 2 мН/м
6. 4. Спирт по каплям вытекает из сосуда через вертикальную трубку внутренним диаметром 2 мм. Считая, что капли отрываются через 1 с одна после другой, найти, через сколько времени вытечет 10 г спирта. Считать диаметр шейки капли в момент отрыва равным внутреннему диаметру трубки.

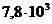 с
с
6. 5. Какую работу А надо совершить, чтобы выдувая мыльный пузырь, увеличить его диаметр от 1 см до 11 см?
3 мДж
6. 6. На сколько давление р воздуха внутри мыльного пузыря больше атмосферного давления р0, если диаметр пузыря равен 5 мм?
62. 5 Па
6. 7. При плавлении нижнего конца вертикально подвешенной свинцовой проволоки диаметром 1 мм образовалось 20 капель свинца. На сколько при этом укоротилась проволока? Коэффициент поверхностного натяжения жидкого свинца 0, 47 н/м. Диаметр шейки капли в момент отрыва считать равным диаметру проволоки.
На 34 см
6. 8. На сколько нагреется капля ртути, полученная от слияния двух капель радиусом 1 мм каждая?
 0C
0C
6. 9. Давление внутри мыльного пузыря на 1 мм рт. ст. больше атмосферного. Чему равен диаметр пузыря? Коэффициент поверхностного натяжения мыльного раствора принять равным 0, 043 Н/м.
2, 6 мм
6. 10. Найти, на какой глубине под водой находится пузырек воздуха, если известно, что плотность воздуха в нем равна 2 кг/м3. Диаметр пузырька 0, 015 мм, температура 200С и атмосферное давление 760 мм рт. ст.
4, 9 м
6. 11. Глицерин поднялся в капиллярной трубке на высоту 20 мм. Определить поверхностное натяжение глицерина, если диаметр капли трубки равен 1 мм.
62 мН/м
6. 12. В воду опущен на очень малую глубину стеклянная трубка с диаметром внутреннего канала, равным 1 мм. Найти массу вошедшей в трубку воды.
23, 1 мм
6. 13. Какую относительную ошибку мы допускаем, вычисляя атмосферное давление, равное 760 мм рт. ст., по высоте ртутного столба, если внутренний диаметр барометрической т рубки равен 5 мм?
0, 4%
6. 14. Разность 
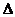 h уровней жидкости в коленах U-образной трубки равна 23 мм. Диаметры d1 и d2 каналов в коленах трубки равны соответственно 2 и 0, 4 мм. Плотность жидкости
h уровней жидкости в коленах U-образной трубки равна 23 мм. Диаметры d1 и d2 каналов в коленах трубки равны соответственно 2 и 0, 4 мм. Плотность жидкости 
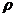 =0, 8 г/см3. Определить поверхностное натяжение жидкости.
=0, 8 г/см3. Определить поверхностное натяжение жидкости.
22, 5 мН/м
6. 15. В жидкость нижним концом опущены две вертикальные капиллярные трубки с внутренними диаметрами d1=0, 05 см и d2=0, 1 см. Разность 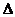 h уровней жидкости в трубках равна 11, 6 мм. Плотность жидкости
h уровней жидкости в трубках равна 11, 6 мм. Плотность жидкости 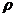 =0, 8 г/см3. Найти поверхностное натяжение жидкости.
=0, 8 г/см3. Найти поверхностное натяжение жидкости.
22 мН/м
6. 16. В воду опущена на очень маленькую глубину стеклянная трубка с диаметром внутреннего канала, равным 1 мм. Найти массу входящей в трубку воды.
23, 1 мг
6. 17. Капиллярная трубка диаметром d= 0, 5 мм наполнена водой. На нижнем конце трубки вода повисла в виде капли. Эту каплю можно принять за часть сферы радиуса r=3 мм. Найти высоту h столба воды в трубке.
6, 37 см
6. 18. На какую высоту h поднимется вода между двумя параллельными друг другу пластинами, если расстояние d между ними равно 0, 2 мм?
7, 3 см
7. Гидродинамика вязкой жидкости
7. 1. Получить распределение скорости течения вязкой жидкости с коэффициентом вязкости 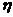 по сечению трубы длиной L и радиуса а, на концах которой создана разность давлений
по сечению трубы длиной L и радиуса а, на концах которой создана разность давлений 
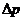 .
.

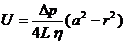
7. 2. Вода течет по круглой гладкой трубе диаметром d=5см со средней скоростью 10 см/с. Определить число Рейнольдса Rе для потока жидкости в трубе и указать характер течения жидкости.
5000
7. 3. По трубе течет машинное масло. Максимальная скорость Vmax, при которой движение масла в этой трубе остается еще ламинарным, равна 3, 2 см/с. При какой скорости движение глицерина в той же трубе переходит из ламинарного вт турбулентное?
1, 94 см/с
7. 4. Самолет летит со скоростью 360 км/ч. Считая, что слой воздуха у крыла самолета, увлекаемый вследствие вязкости, равен 4 см, найти касательную силу, действующую на каждый квадратный метр поверхности крыла. Диаметр молекулы воздуха принять равным 0, 3 нм. Температура воздуха 00С.
45 мН
7. 5. В трубе с внутренним диаметром d=3 см течет вода. Определить максимальный расход воды Qmax при ламинарном течении.
54, 2 г/с
7. 6. Медный шарик диаметром d=1 см падает с постоянной скоростью в касторовом масле. Является ли движение масла, вызванное падением в нем шарика, ламинарным? Критическое значение числа Рейнольдса Reк =0, 5.
Нет
7. 7. Какой наибольшей скорости может достичь дождевая капля диаметром d=0, 3 мм? Диаметр молекулы воздуха принять равным 0, 3 нм, температуру воздуха – 00С. Считать, что для дождевой капли справедлив закон Стокса.
2, 72 м/с
7. 8. Латунный шарик диаметром d=0, 5 мм падает в глицерине. Определить: а) скрость установившегося движения; б) является ли при этой скорости обтекание шарика ламинарным?
6, 71 мм/с; да
III. ТВЕРДЫЕ ТЕЛА
8. Элементы кристаллографии
8. 1. Измеряя массу капли оливкового масла, пущенной на поверхность воды, и площадь, по которой она растеклась, можно приближенно судить о толщине пленки масла. Она примерно равна 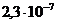 см. Предполагая, что в толщине плёнки укладывается два слоя молекул, найти массу одной молекулы оливкового масла, если плотность масла равна
см. Предполагая, что в толщине плёнки укладывается два слоя молекул, найти массу одной молекулы оливкового масла, если плотность масла равна  г/см3. Зная, что молекулярный вес оливкового масла 884, определить приближенно массу молекулы водорода.
г/см3. Зная, что молекулярный вес оливкового масла 884, определить приближенно массу молекулы водорода.

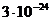 г
г
8. 2. Известно, что нельзя заставить капельку нефти объемом 1 мм3 расплыться по поверхности воды так, чтобы она заняла площадь больше 3 м2. Оцените по этим данным минимальные размеры частиц нефти.
d= 
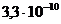 м
м
8. 3. Кристаллическая решетка железа при комнатной температуре – кубическая объемоцентрированная. Атомы железа расположены в вершинах куба и в центре на пересечении пространственных диагоналей куба. Сколько атомов железа приходится на одну элементарную ячейку? Определите постоянную решетки (ребро куба) и минимальное расстояние между атомами железа. Атомная масса железа 55, 9; его плотность 7, 87 г/см3.
|
|
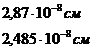
8. 4. Кристаллическая решетка алюминия – кубическая гранецентрированная. Атомы алюминия расположены в вершинах куба и в центре граней. Сколько атомов алюминия приходится на одну элементарную ячейку? Определите постоянную решетки (ребро куба) и минимальное расстояние между атомами алюминия. Атомная масса алюминия 27; его плотность 2, 7 г/см3.
|
|


|
|
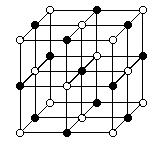
8. 5. Кристаллы поваренной соли NaCl кубической системы состоят из чередующихся атомов (ионов) Na и Cl. Определить наименьшее расстояние между его центрами. Молярная масса 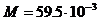 кг/моль, а ее плотность
кг/моль, а ее плотность  кг/м3.
кг/м3.


8. 6. Кристаллы CsCl имеют кубическую объемоцентрированную решетку. В вершинах элементарной ячейки с ребром, равным 0, 41 нм, находятся ионы хлора, в центре ячейки – ион цезия. Найти молярный объем Vм и плотность кристаллов.
42 см3; 4, 1 г/см3
9. Тепловые свойства твердых тел
9. 1. Использовав закон Дюлонга и Пти, определить удельную теплоемкость с: а) меди; б) алюминия.
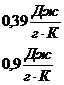
9. 2. Определить по закону равнораспределения внутреннюю энергию U и теплоемкость С кристалла, состоящего из N атомов при температуре Т.
3NkT
9. 3. Используя закон равнораспределения, сравнить теплоемкости 18 г льда (Н2О) и 44 г твердой углекислоты (СО2).
74 и 83 
9. 4. При температуре Т1=40К и Т2=250К для молярной теплоемкости поваренной соли NaCl эксперимент дает С(Т 1)=10, 04  , С (Т2)=48, 86
, С (Т2)=48, 86 
 . При каких температурах для расчета теплоемкости кристаллической поваренной соли можно приближенно пользоваться законом Дюлонга и Пти?
. При каких температурах для расчета теплоемкости кристаллической поваренной соли можно приближенно пользоваться законом Дюлонга и Пти?
При Т 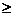 250 К
250 К
10. УПРУГИЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ
10. 1. При растяжении медной проволоки, поперечное сечение которой равно 1, 5 мм2, начало остаточной деформации наблюдалось при нагрузке 4, 5 Н. Каков предел упругости меди?
29, 4 МПа
10. 2. Каким должен быть предельный диаметр стального троса, чтобы он выдерживал нагрузку ?
d=0, 4 мм
10. 3. Для измерения глубины моря с парохода спускали гирю на стальном тросе. Пренебрегая массой гири по сравнению с массой троса, найти, какую наибольшую глубину можно измерить таким способом. Плотность морской воды принять равной 1 г/см3.
11, 9 км
10. 4. К железной проволоке длиной 50 см и диаметром 1 мм привязана гиря массой 1 кг. С каким наибольшим числом оборотов в секунду можно равномерно вращать в вертикальной плоскости такую проволоку с грузом, чтобы она не разорвалась?
3, 4 об/с
10. 5. Имеется резиновый шланг длиной 50 см и внутренним диаметром 1 см. Шланг натянули так, что его длина стала на 10 см больше. Найти внутренний диаметр натянутого шланга, если для резины коэффициент Пуассона равен 0, 5.
9 мм
10. 6. Зеркальце гальванометра подвешено на проволоке длиной 10 см диаметром 0, 01 мм. Найти закручивающий момент, соответствующий отклонению зайчика на 1 мм по шкале, удаленной на 1 м от зеркальца. Модуль сдвига материала проволоки равен  дин/см2.
дин/см2.

 Нм
Нм
10. 7. Найти потенциальную энергию проволоки длиной 5 см и диаметром 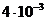 см, закрученной на угол
см, закрученной на угол 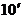 . Модуль сдвига материла проволоки равен
. Модуль сдвига материла проволоки равен 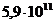 дин/см2.
дин/см2.
10. 8. Найти значение коэффициента Пуассона, при котором объем проволоки при растяжении не меняется.
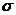 =0, 5
=0, 5
10. 9. Найти относительное изменение плотности цилиндрического медного стержня при его сжатии давлением р=1000 Н/м2. Коэффициент Пуассона для меди равен 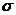 =0, 34.
=0, 34.
0, 027%
10. 10. Железная проволока длиной 5 м висит вертикально. На сколько изменится объем проволоки, если к ней привязать гирю массой 10 кг? Коэффициент Пуассона для железа взять равным 0, 3.
На 1 мм3
11. ФАЗОВЫЕ ПРЕВРАЩЕНИЯ
11. 1. 
 На рисунке показана точка А на кривой упругости насыщенного пара некоторого вещества. Что соответствует этой точке на диаграмме P, V?
На рисунке показана точка А на кривой упругости насыщенного пара некоторого вещества. Что соответствует этой точке на диаграмме P, V?
Р
 К
К
А
Тр

Т
11. 2. На рисунке показан участок изотермы, отвечающий переходу некоторого вещества из кристаллического состояния в жидкое состояние. Что соответствует этому участку на диаграмме Р, Т?
Р
кристалл жидкость
жидкость+ кристалл
V
11. 3. 






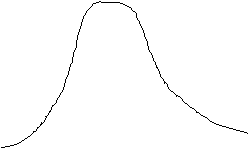



 На рисунке изображены три изотермы и изобара.
На рисунке изображены три изотермы и изобара.
Р Т2
Р1
Тк
Т1
V
А) Изобразить эти линии на диаграмме Р, Т, приведенной ниже.

 Р
Р

 К
К


 Тр
Тр
Т
Б) Что соответствует на диаграмме Р, Т области, расположенной под купо-
лообразной кривой на предыдущем рисунке?
11. 4. Определить характер зависимости (убывает, возрастает и т. п. ) давления насыщенного пара от температуры. Где начинается и где кончается кривая испарения Р(Т)? Изобразить качественно кривую испарения на диаграмме (Р, Т).
11. 5. 






 Какие процессы будут идти в термодинамически равновесной системе, изображенной на рисунке, если поршень: а) поднимать; б)опускать? Система термостатирована при температуре Т.
Какие процессы будут идти в термодинамически равновесной системе, изображенной на рисунке, если поршень: а) поднимать; б)опускать? Система термостатирована при температуре Т.
1
2
Изобразить эти процессы на диаграмме (Р, V), начальное двухфазное состояние системы помечено крестом.
Р
 Кр. т Р
Кр. т Р
х

 Тр. т
Тр. т
Т V
11. 6. Расплавленный свинец нагрели до температуры То выше температуры плавления Тпл и отключили нагреватель. Качественно нарисовать зависимость температуры свинца от времени. Указать моменты времени начала и конца кристаллизации
11. 7. Суммарная масса жидкости и ее насыщенного пара m=12 кг. Определить приближенно массу жидкости mж и массу пара mп, если система находится в равновесном состоянии, изображенном крестом.
 Р
Р


 х
х
 I I I I I I I I I I
I I I I I I I I I I
V
11. 8. 





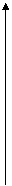
 На рисунке дана изотерма некоторого вещества. Горизонтальный участок изотермы соответствует двухфазным состояниям «жидкость + насыщенный пар». Известны: температура Т, давление насыщенного пара Рн. п при этой температуре, масса вещества m, удельная теплота испарения q12, удельные объемы
На рисунке дана изотерма некоторого вещества. Горизонтальный участок изотермы соответствует двухфазным состояниям «жидкость + насыщенный пар». Известны: температура Т, давление насыщенного пара Рн. п при этой температуре, масса вещества m, удельная теплота испарения q12, удельные объемы  жидкости и
жидкости и 
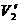 насыщенного пара. Найти: а) работу А12, совершенную веществом при переходе из состояния 1 в состояние 2; б) количество теплоты Q12, полученное при этом переходе; в) приращение внутренней энергии U2- U1.
насыщенного пара. Найти: а) работу А12, совершенную веществом при переходе из состояния 1 в состояние 2; б) количество теплоты Q12, полученное при этом переходе; в) приращение внутренней энергии U2- U1.
Р
Рн. п
V1 V2 V
11. 9. Удельные объемы газовой и жидкой фазы некоторого вещества при давлении Р равны Vг и Vж соответственно. Удельная теплота испарения при этом давлении q. Найти приращение удельной внутренней энергии вещества при испарении. Чему равна скрытая теплота парообразования в критической точке?

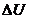 =q- Р(Vг – Vж)
=q- Р(Vг – Vж)
нулю
11. 10. Используя уравнение Клапейрона-Клаузиуса при известных q, Vж, и Vг найти зависимость Р(Т) при условии, что q= const, Vг > > Vж и что можно с достаточной степенью точности применять уравнение состояния идеального газа.

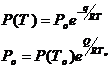

|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|