Контакты

Случайная статья

3.3 Сборник задач

⇐ ПредыдущаяСтр 3 из 4Следующая ⇒

3. 3 Сборник задач

Упражнение 1. Неравенство Йенсена:

1. Докажите неравенство 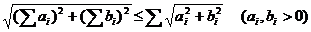, (подсказка: ).

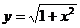2. Докажите неравенство , где .

3. Докажите неравенство 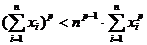, при .

Упражнение 2. Неравенство Коши-Буняковского:

1. Доказать, что , где a, b, c – стороны треугольника; h_a, h_b, h_c – высоты треугольника, опущенные на эти стороны; S – площадь треугольника.

2. Доказать, что , .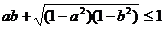

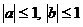3. Доказать, что , если .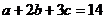

Упражнение 3. Неравенство Коши:

1. Для неотрицательных a, b, c выполняется условие a²+b²+c²=1. Доказать, что .

2. Дано: a, b, c≥ 0, a+b+c=1. Доказать неравенство: .

3. Доказать: .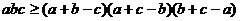

4. Дано: x, y, z> 0, xyz=1. Доказать .

Упражнение 4. Неравенство Бернулли:

1. Решить уравнение: .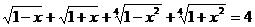

2. Решить уравнение: .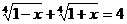

3. Решить уравнение: .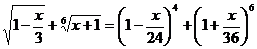

Упражнение 5. Весовое (общее) неравенство Коши:

1. Доказать неравенство , если .

2. Доказать неравенство: .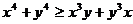

3. Доказать неравенство: .

3. 4 Тесты

1. Какая зависимость между коэффициентами α _i в неравенстве Йенсена

?

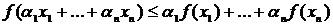а) их произведение равно единице

б) их сумма равна единице

в) они равны между собой

г) никакой

2. Как доказать неравенство Коши-Буняковского?

а) доказать неравенство Йенсена для функции

б) применить неравенство Коши для n чисел

в) доказать методом математической индукции

г) путем алгебраических преобразований

3. Когда достигается равенство в неравенстве Коши?

а) когда сумма всех чисел равна их количеству

б) когда их произведение равно единице

в) когда все числа равны между собой

г) никогда

4. В неравенстве Бернулли x – переменная – может быть…

а) любым числом

б) строго меньше нуля

в) строго больше нуля

г) строго больше минус единицы

5. В каком случае весовое неравенство Коши превращается в классическое неравенство Коши?

а) когда все переменные равны между собой

б) когда все весовые коэффициенты равны между собой

в) когда произведение весовых коэффициентов равно единице

г) когда сумма весовых коэффициентов равна единице

6. С помощью какого неравенства лучше доказывать неравенство

?

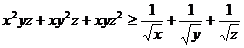а) с помощью неравенства Коши

б) с помощью неравенства Бернулли

в) с помощью неравенства Йенсена

г) с помощью неравенства Коши-Буняковского

7. Какую надо применить функцию в неравенстве Йенсена, чтобы доказать

?

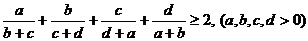а)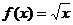

б)

в)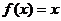

г)

8. Чему равны весовые коэффициенты в неравенстве ?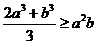

а)

б)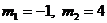

в)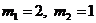

г)

9. Какое неравенство доказывается с помощью неравенства Коши-Буняковского?

а)

б)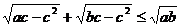

в)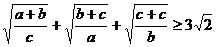

г) .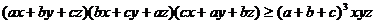

⇐ Предыдущая 1 234 Следующая ⇒

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.