Решение задач

⇐ ПредыдущаяСтр 2 из 4Следующая ⇒

Задача:

Пусть a₁, …, a_n > 0, 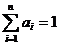. Доказать .

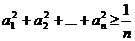Решение:

Записываем неравенство Йенсена для f(x)=x², m_i=n. Получаем:

, , ,

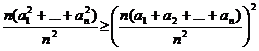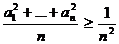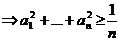что и требовалось доказать.

Неравенство Коши-Буняковского

Задача:

Пусть a+b+c=1. Доказать, что .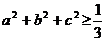

Решение:

Из неравенства Коши-Буняковского имеем

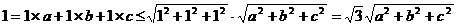А отсюда имеем, что .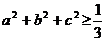

Неравенство Коши

Задача:

Пусть a, b, c – положительные числа, сумма которых равна единице. Доказать, что

(1+a)(1+b)(1+c) ≥ 8(1-a)(1-b)(1-c).

Решение:

Поскольку a+b+c=1, то 1+a= (1-b)+(1- c). Используя неравенство Коши между средним арифметическим и средним геометрическим 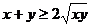, получаем

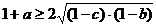Аналогично

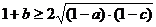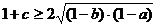Перемножая все три неравенства, получаем искомое неравенство.

Неравенство Бернулли

Задача:

Решить уравнение

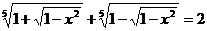Решение:

К каждому слагаемому левой части уравнения применяем неравенство Бернулли, тогда

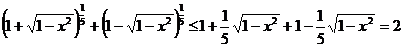причем равенство возможно лишь при 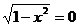, т. е. x=±1. Следовательно, x=±1 – корни уравнения.

Весовое (общее) неравенство Коши

Задача 1:

Для действительных положительных чисел a, b доказать неравенство .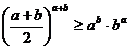

Решение:

По весовому неравенству Коши ( 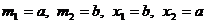), имеем

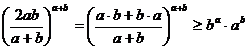Для завершения доказательства осталось учесть очевидное неравенство 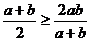. Равенство достигается при a=b.

Задача 2:

Для произвольных a, b≥ 0 доказать неравенство

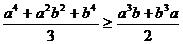(1).

Решение:

По весовому неравенству Коши имеем, что

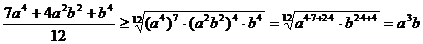Добавляя к указанному неравенству аналогичное

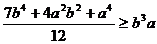
получаем

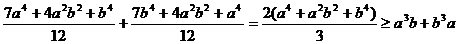что и требовалось доказать. Равенство в (1) достигается при a=b.

Понятно, что решение этой задачи состоит из двух ключевых идей. Первая – это неравенство (2). Вторая – переход от неравенства (2) к неравенству (1).

Что касается неравенства (2), то пока ещё не понятно, как можно было «угадать», что для решения задачи надо было использовать неравенство Коши именно с такими весовыми коэффициентами m₁=7, m₂=4, m₃=1.

Покажем, что эти коэффициенты можно найти (именно так они и были найдены) с помощью стандартной процедуры: «метода неопределённых коэффициентов». Неравенство (2) будем искать из таких соображений. Рассмотрим весовое неравенство Коши

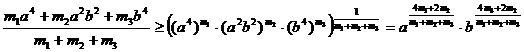. (4)

Подберём весовые коэффициенты m₁, m₂, m₃ так, чтобы в правой части неравенства (4) получить a³b. Для этого достаточно решить систему

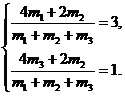(5)

Кроме этого, если к (4) добавить аналогичное неравенство (в решении задачи это было неравенство (3))

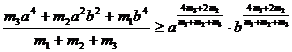, (6)

то получим

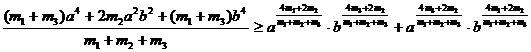. (7)

Следовательно, чтобы неравенство (7) совпало с неравенством в задаче, к системе (5) надо прибавить еще два равенства

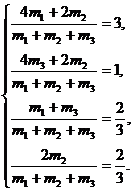(8)

Решая систему (8), имеем m₁=7 m₃, m₂=4 m₃. При таком подборе m₁, m₂, m₃ неравенство (4) становится неравенством (2), неравенство (6) – неравенством (3), а неравенство (7) – неравенством (1).

Подводя итоги сказанному, мы видим, что для доказательства неравенства типа (1) записываем общее весовое неравенство Коши с неопределенными весовыми коэффициентами, где слева стоят все слагаемые левой части, а справа – одно слагаемое правой части искомого неравенства. Подбираем неопределенные коэффициенты (путем решения соответствующей системы равенств) так, чтобы после симметризации весового неравенства найти решение задачи.

⇐ Предыдущая 123 4 Следующая ⇒