№5-2. Основные методы изучения взаимосвязей

Корреляцию и регрессию принято рассматривать как совокупный процесс статистического исследования, поэтому их использование в статистике часто именуют корреляционно-регрессионным анализом.

Корреляционно-регрессионный анализ используется для исследования форм связи, устанавливающих количественные соотношения между случайными величинами изучаемого процесса.

Для изучения, измерения и количественного выражения взаимосвязей между явлениями статистикой применяются различные методы, важнейшим из которых являются: метод сопоставления, метод параллельных рядов, балансовый, графический, методы аналитических группировок, дисперсионного и корреляционного анализа.

В данной работе при решении задачи мы используем несколько методов.

№1-Задача: По группе акционерных коммерческих банков региона имеются следующие данные:

№ банка	Активы банка, млн. руб	Прибыль, млн. руб
		3, 4
		4, 2
		3, 8
		5, 9
		6, 0
		5, 8
		5, 6
		6, 3
		6, 9
		6, 9
		8, 2
		7, 7
		8, 5
		8, 0
		9, 6
		10, 1
		12, 0
		11, 6
		13, 4
		15, 8
		16, 2
		17, 4
		16, 5
		19, 0
		23, 4
		22, 6
		20, 7
		26, 3
		32, 0
		31, 5

Установить направление и характер взаимосвязи между суммой прибыли банка и размером его активов. Полученную корреляционно-регрессионную модель проверить на адекватность.

Решение:

1. В исходных данных задачи таблица представлена в виде метода сопоставления параллельных рядов.

Метод параллельных рядов– ряд значений факторного признака и соответствующих ему значений результативного признака (значение признака Х располагается в возрастающем порядке, затем прослеживают направление изменения величины результативного признака Y). Чтобы установить связь между явлениями, достаточно расположить полученные в результате сводки и обработки материалы в виде параллельных рядов и сопоставить их между собой. Такое сопоставление, проведенное после теоретического анализа, показавшего возможность связи между изучаемыми явлениями, позволяет проследить числовые соотношения сопоставляемых признаков и направление их изменений, т. е. позволяет установить наличие связи и получить представление о ее характере.

№2- 2. Применим метод построения групповой таблицы.

Метод аналитических группировок. Сущность этого метода заключается в том, что единицы статистической совокупности группируются, как правило, по факторному признаку и для каждой группы исчисляется средняя или относительная величина по результативному признаку.

Все наблюдения разбиваются на группы в зависимости от величины факторного признака и по каждой группе вычисляется среднее значение результативного признака.

Группа банков по активам, млн. руб	Число банков в группе	Средняя прибыль в данных группах банков, млн. руб
		3, 8
		5, 95
		6, 15
		7, 55
		8, 78
		11, 8
		15, 13
		16, 95
		21, 2
		23, 2
		31, 75
-		-

С увеличением активов банков увеличивается прибыль, т. е. предполагается наличие прямой связи.

№6- 3. Балансовый метод. Сущность метода заключается в том, что данные взаимосвязанных показателей изображаются в виде таблицы и располагаются таким образом, чтобы итоги между отдельными частями были равны, т. е. чтобы был баланс. Этот метод используется для характеристики взаимосвязи между производством и реализацией продукции, денежными доходами и расходами населения и т. д.

Составим корреляционную таблицу. Построение начинается с группировки значений факторного и результативного признаков.

Для группировки значений результативного признака определим величину интервала группировки

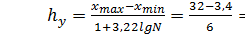(млн. руб)

Середина интервала, y	5, 785	10, 565	15, 345	20, 125	24, 905	29, 685
Гр по y Гр по x	3, 4-8, 17	8, 18-12, 95	12, 96-17, 73	17, 74-22, 51	22, 52-27, 29	27, 3-32, 07
							5, 785
							5, 785
							5, 785
							8, 175
							8, 653
							10, 565
							15, 345
							15, 345
							22, 515
							23, 312
							29, 685
f_y							-

частота повторения значений факторного и результативного признаков соответственно, по всей совокупности.

среднее значение результативного признака для «j» группы значения факторного признака.

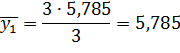
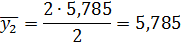
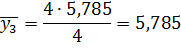
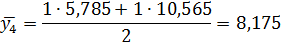
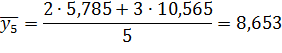
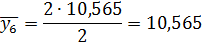
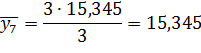
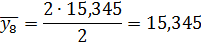
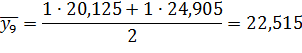
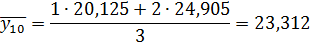
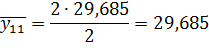
Числа, расположенные на пересечении строк и столбцов таблицы означают частоту повторения данного сочетания значений х и у.

Если частоты в корреляционной таблице располагаются по диагонали из левого верхнего угла в правый нижний угол, то предполагают наличие прямой связи.

В данной задаче мы видим наличие прямой связи.

Увеличение среднего значения у с увеличением факторного свидетельствует о возможном наличии прямой корреляционной зависимости прибыли от суммы активов банка.

Построим графики полученных результатов с использованием трех методов. Мы видим, что характер функции близок к прямолинейной.

№3- 4. Аналитический метод

Изучение корреляционных зависимостей основывается на исследовании таких связей между переменными, при которых значение одной переменной можно принять за зависимую переменную, которая «в среднем» изменяется в зависимости от того, какие значения принимает другая переменная, рассматриваемая как причина изменения зависимой переменной. Действие данной причины осуществляется в условиях сложного взаимодействия различных факторов, вследствие чего проявление закономерности затемняется влиянием случайностей. Вычисляя средние значения результативного признака для данной группы значенийпризнака-фактора, мы отчасти исключаем влияние случайностей. Вычисляя параметры теоретической линии связи, мы производим дальнейшее их исключение и получаем однозначное (по форме) изменение переменной у с изменением фактора х.

Теоретической линией регрессии – называется линия, вокруг которой группируются точкикорреляционного поля и которая указывает основное направление, основную тенденцию связи.

Теоретическая линия регрессии должна отображать изменение средних величин результативного признака y по мере изменения величин факторного признака х при условии полного взаимопогашения всех прочих случайных по отношению к фактору х причин. Следовательно, эта линия должна быть проведена так, чтобы сумма отклонений точек поля корреляции от соответствующих точек теоретической линии регрессии равнялась нулю, а сумма квадратов этих отклонений была бы минимальной величиной.

№4- Важным этапом регрессионного анализа является определение типа функции, с помощью которой характеризуется зависимость между признаками. Главным основанием для выбора вида уравнения должен служить содержательный анализ природы изучаемой зависимости, ее механизма. На основе теоретического анализа нередко могут быть сделаны самые общие выводы относительно направления связи, возможности его изменения в исследуемой совокупности, правомерности использования линейной зависимости, возможного наличия экстремальных значений и т. п. Необходимым дополнением такого рода предположений должен быть анализ конкретных фактических данных.

Тип уравнения выбирается на основе теоретического анализа и исследования фактических данных. В большинстве случаев связи в общественных явлениях изучают по уравнению прямой, вида 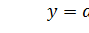, где a и b – параметры искомой прямой.

Данное уравнение – уравнение регрессии, а сама прямая называется линией регрессии. Параметры уравнения a и b находятся выравниванием по способу наименьших квадратов, которые приводят к системе двух нормальных уравнений:

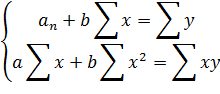
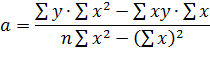
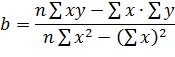
Для измерения тесноты линейной зависимости рассчитывают линейный коэффициент корреляции ( ).

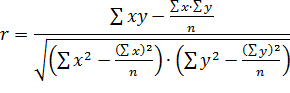
или

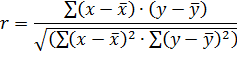
№6- При расчете этого показателя учитываются не только знаки отклонений индивидуальных значений признака от средней, но и сама величина таких отклонений, т. е. соответственно для факторного и результативного признаков определяют величины 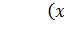и .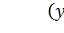

При пользовании формулой расчета линейного коэффициента корреляцииотпадает необходимость вычислять отклонения индивидуальных значений признаков от средней величины, что исключает ошибку в расчетах при округлении средних величин.

Линейный коэффициент корреляции может принимать любые значения в пределах от -1 до +1. Чем ближе коэффициент корреляции по абсолютной величине к 1, тем теснее связь между признаками. Знак при линейном коэффициенте корреляции указывает на направление связи: прямой зависимости соответствует знак «+», а обратной зависимости – знак «-».

Если с увеличением значений факторного признака результативный признак имеет тенденцию к увеличению, то величина коэффициента корреляции будет находиться между 0 и 1.

Зная коэффициент корреляции, можно дать качественно-количественную оценку тесноты связи. Используются, например, специальные табличные соотношения (так называемая шкала Чеддока).

Для удобства расчетов составим таблицу и занесем в нее данные.

Подставив все значения в формулу линейного коэффициента корреляции, получаем что r = 0, 959.

|r|> 0, 9, следовательно - связь между признаками прямая и очень сильная.

№5-3. Проверка на адекватность регрессионной модели

Для практического использования моделей регрессии очень важна их адекватность, т. е. соответствие фактическим данным. Поскольку корреляционно-регрессионный анализ обычно проводится для ограниченной по объему совокупности, то параметры уравнения регрессии, коэффициента корреляции могут быть искажены действием случайных факторов.

Чтобы проверить на сколько эти показатели характерны для всей генеральной совокупности, необходимо проверить адекватность построенных статистических моделей. Проверка значимости (существенности) осуществляется с помощью t-критерия Стьюдента. При этом рассчитываются значения t-критерия:

- для параметра a: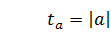

- для параметра b: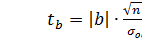

Параметры a и b могут быть как положительные, так и отрицательные, берутся по модулю.

№6- Средняя квадратическая ошибка уравнения дает нам возможность в каждом отдельном случае с определенной вероятностью указать, что величина результативного признака расположена в определенном интервале относительно значения, вычисленного по уравнению регрессии.

– остаточное среднее квадратическое отклонение результативного признака у от выровненных значений

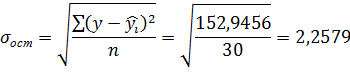
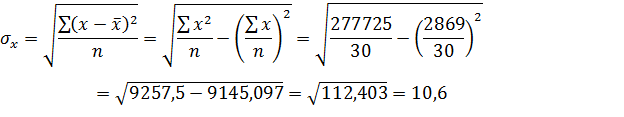
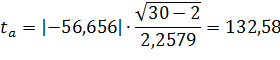
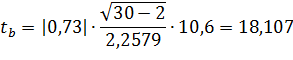
Вычисленные значения сравниваем с критическим t, которое определяется по таблице распределения Стьюдента, с учетом принятого уровня значимости 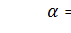и числа степеней свободы , что соответствует = 2, 048.

Параметр признается значимым при условии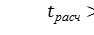

В нашем случае 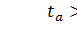и 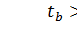значит параметры уравнения регрессии признаются значимыми.

Для линейной однофакторной связи используется формула

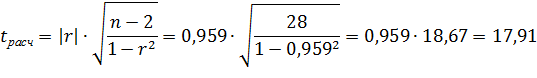
, что свидетельствует о значимости линейного коэффициента корреляции и существенности связи между активами банка и прибылью.

Таким образом, построенная модель в целом адекватна.

Данные, полученные по результатам малой выборки можно с достаточной вероятностью распространить на всю гипотетическую генеральную совокупность.

№2-4. Экономическая интерпретация параметров уравнения регрессии

После проверки адекватности, установления точности и надежности построенной модели (уравнения регрессии), ее необходимо проанализировать. Прежде всего нужно проверить, согласуются ли знаки параметров с теоретическими представлениями и соображениями о направлении влияния признака-фактора на результативный признак (показатель).

В рассмотренном уравнении 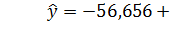, характеризующем зависимость размера прибыли банков (у) от активов банков (х).

Параметр b> 0, следовательно, с возрастанием активов банков размер прибыли увеличивается.

Из уравнения следует, что возрастание активов банков на1 млн рублей приводит к увеличению прибыли банков в среднем на 0, 73 млн рублей

№6- Для оценки влияния факторного признака на результативный рассчитывается коэффициент эластичности в целом для всей совокупности. Он показывает средние изменения результативного признака при изменении факторного признака на 1% и вычисляется по формуле:

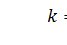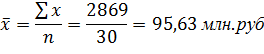
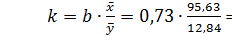Коэффициент рассчитывается в процентах.

По полученным результатам можно сделать вывод, что при увеличении активов банка на 1% увеличивается прибыль на 5, 44%.

№3-Заключение

Таким образом, в данной работе установлена корреляционная зависимостьпоказателей 30 российских банков, проведен регрессионный анализ и найдена регрессионная модель данной взаимосвязи показателей.

Полученное уравнение 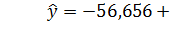позволяет проиллюстрировать зависимость размера прибыли банков от размера их активов.

А также проведена проверка данной модели на адекватность по критерию Стьюдента, результат оказался положительным (модель адекватна, т. е. ее можно применять), а затем дана экономическая оценка этой модели - при увеличении активов банка увеличивается и прибыль.

⇐ Предыдущая 12