Первообразная. Неопределенный интеграл.

Лекция

Первообразная. Неопределенный интеграл.

Интегральное исчисление – это нахождение новой функции, производная которой равна заданной функции. Функцию, восстанавливаемую по заданной ее производной или дифференциалу, называют первообразной

1. Первообразная.

Определение: Дифференцируемая функция 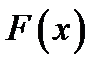, определенная на некотором промежутке Х, называется первообразной для функции 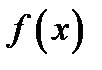, определенной на том же промежутке, если для всех х из этого промежутка 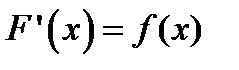, или, что то же самое, .

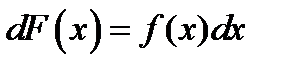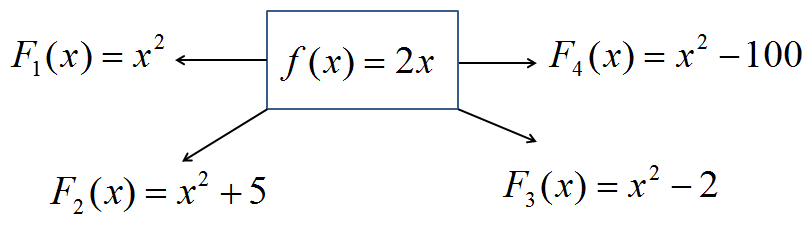
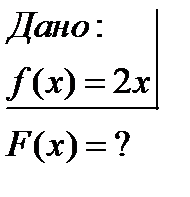
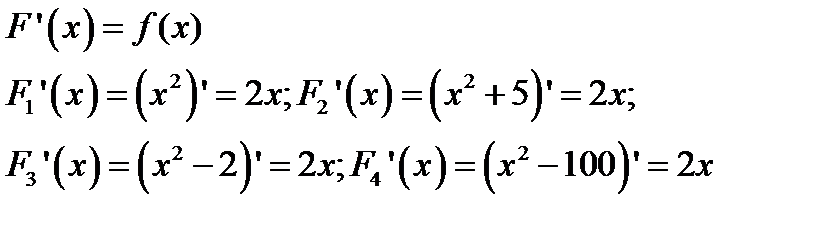
Дифференцирование функции – однозначная операция, т. е. если функция имеет производную, но только одну. Это утверждение непосредственно следует из определения предела и производной: если функция имеет предел, то толь один. Обратная операция – отыскание первообразной – не однозначна. Из примера, любые две первообразные 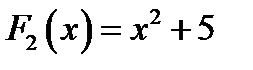  и 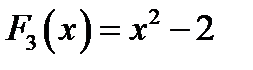  данной функции отличаются друг от друга на постоянное слагаемое.

Теорема: Если 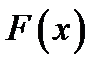  является первообразной функции  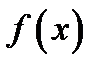  на некотором промежутке, то множество всех первообразных этой функции имеет вид 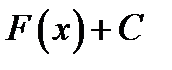, где С- любое действительное число.

2. Неопределенный интеграл.

Определение: Совокупность всех первообразных для функции 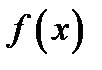, определенных на некотором промежутке Х, называется неопределенным интегралом от функции  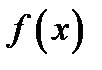 на этом промежутке.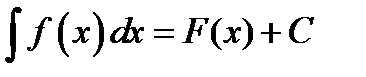

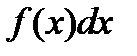-подынтегральное выражение; - подынтегральная функция; х – переменная интегрирования; 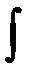- знак неопределенного интеграла; С – постоянная интегрирования.

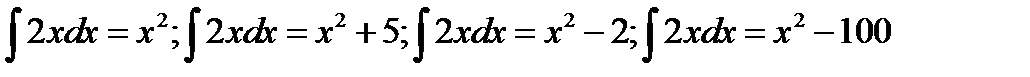
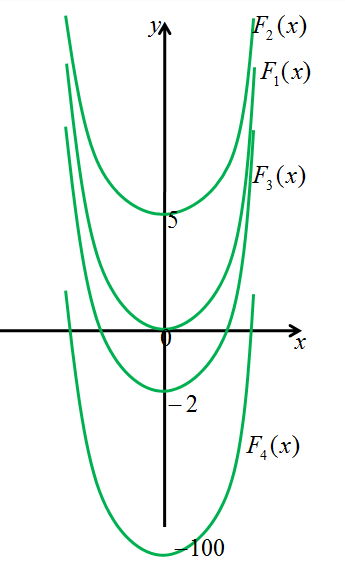
Геометрический смысл: Неопределенный интеграл представляет собой семейство интегральных кривых, каждая из которых получается из любой другой кривой параллельным переносом вдоль оси ординат.

Основные свойства

Словесная формулировка Математическая запись

1. Производная неопределенного интеграла равна подынтегральной функции.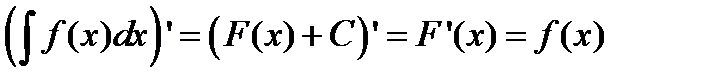

2. Дифференциал неопределенного интеграла равен подынтегральному выражению.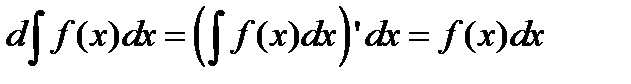

3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная.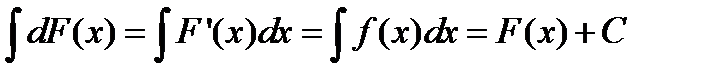

4. Постоянный множитель можно выносить за знак интеграла.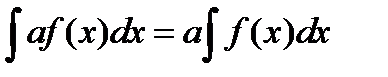

5. Неопределенный интеграл от алгебраической суммы двух непрерывных функций равен алгебраической сумме интегралов от этих функций в отдельности.

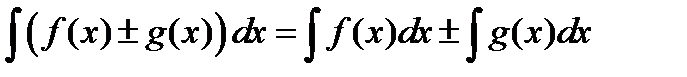
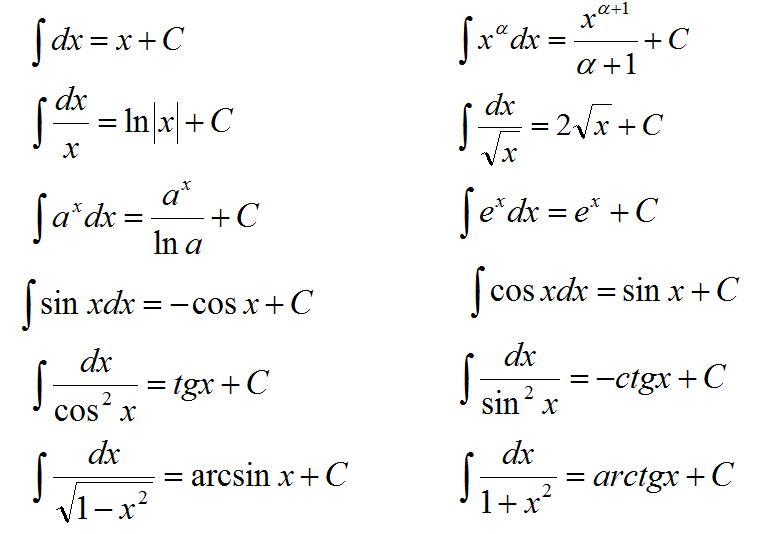Табличные интегралы:

12 Следующая ⇒