Главная

Контакты

Случайная статья

• Автоматизация
• Антропология
• Археология
• Архитектура
• Биология
• Ботаника
• Бухгалтерия
• Военная наука
• Генетика
• География
• Геология
• Демография
• Деревообработка
• Журналистика
• Зоология
• Изобретательство
• Информатика
• Искусство
• История
• Кинематография
• Компьютеризация
• Косметика
• Кулинария
• Культура
• Лексикология
• Лингвистика
• Литература
• Логика
• Маркетинг
• Математика
• Материаловедение
• Медицина
• Менеджмент
• Металлургия
• Метрология
• Механика
• Музыка
• Науковедение
• Образование
• Охрана Труда
• Педагогика
• Полиграфия
• Политология
• Право
• Предпринимательство
• Приборостроение
• Программирование
• Производство
• Промышленность
• Психология
• Радиосвязь
• Религия
• Риторика
• Социология
• Спорт
• Стандартизация
• Статистика
• Строительство
• Технологии
• Торговля
• Транспорт
• Фармакология
• Физика
• Физиология
• Философия
• Финансы
• Химия
• Хозяйство
• Черчение
• Экология
• Экономика
• Электроника
• Электротехника
• Энергетика

1.3 Варианты заданий. Вариант № 1. Вариант № 2. Вариант № 3. Вариант №5. Вариант № 6. Вариант № 7. Вариант № 8. Вариант № 9. Вариант № 10. Вариант № 11. Вариант № 12. Вариант № 13. Вариант № 14. Вариант № 15. Вариант № 16. Вариант № 17. Вариант № 18. Вари

1. 3 Варианты заданий

Для заданного ряда необходимо вычислить с точностью e  бесконечную сумму и указать количество учтенных слагаемых (слагаемые, меньшие e в сумму не включать).

Разработать и реализовать два алгоритма вычисления члена ряда:

• по формуле общего члена ряда;
• с использованием рекуррентной формулы.

Вариант № 1

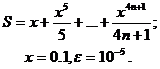
Вариант № 2

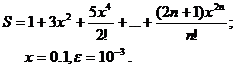
Вариант № 3

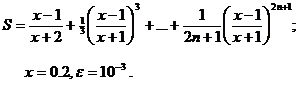
Вариант № 4

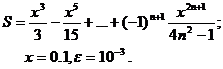
Вариант №5

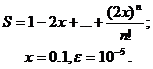
Вариант № 6

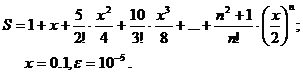
Вариант № 7

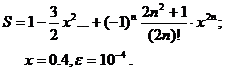
Вариант № 8

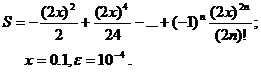
Вариант № 9

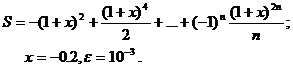
Вариант № 10

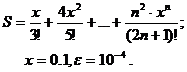
Вариант № 11

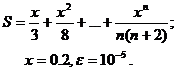
Вариант № 12

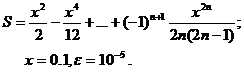
Вариант № 13

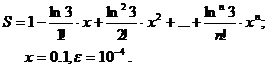
Вариант № 14

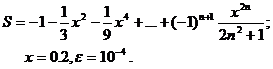
Вариант № 15

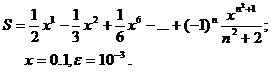
Вариант № 16

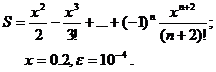
Вариант № 17

Вариант № 18

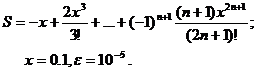
Вариант № 19

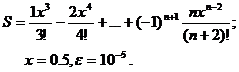
Вариант № 20

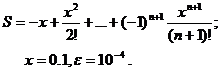
Вариант № 21

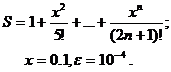
В вариантах 22 -28 вычислить значение суммы членов бесконечного ряда (таблица 1. 1) с заданной точностью 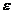. На печать вывести значение суммы и число членов ряда, вошедших в сумму. Для проверки полученного результата осуществить вызов функции, разложенной в бесконечный ряд.

Таблица 1. 1  

Варианты заданий

№ Вар.	Функция	Сумма членов ряда	Значен.  х	Точность
	2	3	4	5
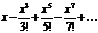
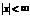
	sinx			10-4
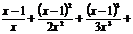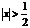
	lnx	…		10-5
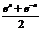
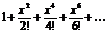
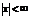
	chx:			10-4
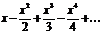
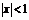
	ln(1+x)			10-5
	сos	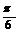	_	10-4
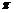
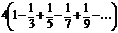
			_	10-4
	cos2x		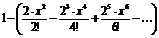_	10-5

1. 4 Контрольные вопросы

1. Что такое итерационный цикл? Его отличия от цикла с заданным числом повторений.
2. Какие операторы цикла организуют итерационный циклический процесс?

3. Каково условие выхода из цикла при вычислении значения суммы бесконечного ряда?

4. Почему при вычислении значения текущего члена a_n используется простая переменная, а не индексированная?

5. Что такое рекуррентная формула? Каково ее назначение?