
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
1. ИССЛЕДОВАНИЕ итерационныХ алгоритмоВ
1. ИССЛЕДОВАНИЕ итерационныХ алгоритмоВ
Цель работы – изучить основные алгоритмы организации итерационных циклов, овладеть практическими навыками разработки, программирования и применения итерационного циклического вычислительного процесса.
1. 1 Подготовка к лабораторной работе
При подготовке к лабораторной работе необходимо ознакомиться с организацией циклов, изучить операторы для реализации циклов.
1. 2 Теоретические сведения
Циклы с заранее неизвестным числом повторений, которые выполняются, пока истинны определенные условия, называются итерационными.
Алгоритм, в состав которого входит итерационный цикл, называется итерационнымалгоритмом. Итерационные алгоритмы используются при реализации итерационных численных методов.
В итерационных алгоритмах необходимо обеспечить обязательное достижение условия выхода из цикла (сходимость итерационного процесса). В противном случае произойдет зацикливание алгоритма, т. е. не будет выполняться основное свойство алгоритма — результативность.
Условиями окончания цикла могут быть: достижение заданной точности вычисления результата, изменение знака определенной величины и т. д.
Вычисление суммы бесконечного ряда с заданной точностью является типичной задачей, использующей итерационный цикл, так, как заранее не известно, при каком члене ряда будет достигнута требуемая точность.
Пусть бесконечная сумма имеет вид: 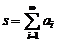 . Каждое слагаемое суммы является функцией от номера i, определяющего место этого слагаемого в сумме, а также может являться функцией одного или нескольких дополнительных параметров.
. Каждое слагаемое суммы является функцией от номера i, определяющего место этого слагаемого в сумме, а также может являться функцией одного или нескольких дополнительных параметров.
Вычисление суммы ряда состоит в получении в результате циклического процесса последовательности s1, s2, …, si, …, сходящейся к своему предельному значению. В общем случае начальное значение номера члена ряда i может быть отличным от 1 (например, равным 0). Суммирование считается законченным при выполнении условия достижения заданной точности 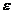 :
: 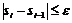 или
или 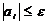 .
.
Алгоритм 1. Каждый член суммы аi вычисляется по формуле общего члена ряда.
Пример 1. 1. Пусть x – некоторое число, а e = 0. 001. Вычислить сумму элементов бесконечно убывающей знакопеременной последовательности {an}, где an=(-1)n(2x)n/n!, удовлетворяющих условию |an| > e, n=1, 2…. Определить количество слагаемых. Вывести на экран результаты вычислений.
Схема алгоритма решения этой задачи приведена на рис. 1. 1.
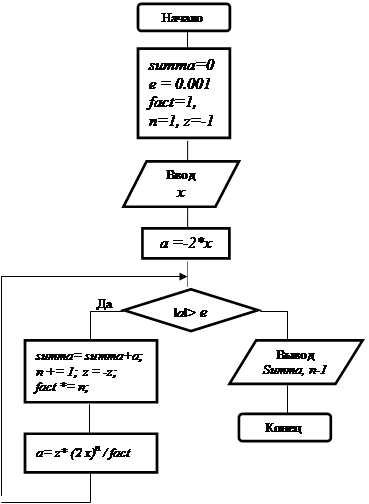
Рис. 1. 1. Схема алгоритма решения задачи 1. 1
Программа будет иметь вид:
#include " stdafx. h"
#include < iostream>
#include < windows. h>
#include < math. h>
#include < conio. h> // Файл, где определена функция getch()
using namespace std;
int main()
{
SetConsoleOutputCP(1251);
//Сначала сумма равна нулю, а факториал единице
double summa=0, x, a, e = 0. 001;
int fact=1, n=1, z=-1;
cout< < " Введите число x: \n";
cin> > x;
a =-2*x;
while (abs(a) > e)
{summa = summa + a;
n += 1; //Вычисляем an+1}
z = -z; //Вычисляем (-1)n+1}
fact *= n; //Вычисляем факториал}
a = z * pow(2 * x, n) / fact; //См. Замечание}
}
cout< < " Суммa =" < < summa< < " \n";
cout< < " Количество слагаемых =" < < n-1;
getch();
return 0;
}
Замечание. Вычисление знакопеременной суммы возможно при помощи следующей конструкции:
if (n % 2! =0) summa=summa – a else summa = summa+a
Существует более экономный способ вычисления значения переменной а (элемента именно данной последовательности), используя предыдущее значение и команду присваивания вида a=a*M, где для данного примера M =- x/(n+1) (коэффициент рекуррентности).
Алгоритм 2. Если в формулу общего члена суммы входят степени и факториалы, то для уменьшения затрат времени на вычисление текущего члена ряда целесообразно использовать рекуррентную формулу.
Для получения рекуррентной формулы используется отношение текущего члена ряда к предыдущему: 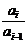 .
.
Пример 1. 2. Требуется вычислить сумму ряда 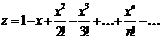 с точностью
с точностью  .
.
Для получения рекуррентной формулы (коэффициента рекуррентности) используем отношение текущего члена ряда к предыдущему:
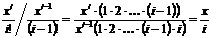 . Тогда
. Тогда 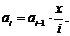 Точность будет достигнута, если
Точность будет достигнута, если 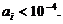
Схема алгоритма решения этой задачи приведена на рис. 1. 2.
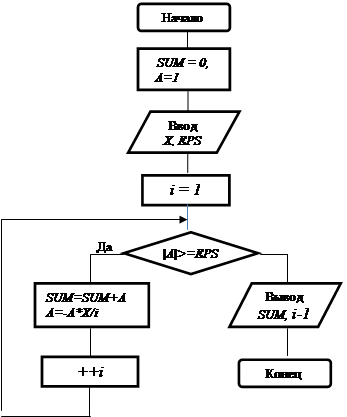
Рис. 1. 2. Схема алгоритма решения задачи 1. 2
Программа будет иметь вид:
#include " stdafx. h"
#include < iostream>
#include < windows. h>
#include < math. h>
#include < conio. h> // файл, где определена функция getch()
using namespace std;
int main()
{SetConsoleOutputCP(1251);
//Сначала сумма равна нулю
double SUM = 0, X, EPS, A=1;
int i;
cout< < " Введите Х\n";
cin> > X;
cout< < " Введите ТОЧНОСТЬ\n";
cin> > EPS;
//Считать сумму членов ряда пока 
for ( i = 1; abs(A)> =EPS; ++i)
{
SUM=SUM+A; // суммирование
A=-A*X/i; // следующий элемент ряда (X/i-коэффициент рекуррентности)
}
cout< < " СУММА=" < < SUM;
cout< < " \nКОЛИЧЕСТВО СЛАГАЕМЫХ =" < < i-1;
getch(); // ждать нажатия любой клавиши
return 0;
}
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|