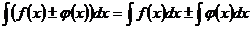- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ.
Задача 1. Вычислить пределы:
а) 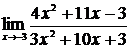 ; б)
; б) 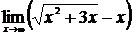 ;
;
в) 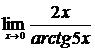 ; г)
; г) 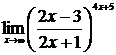 .
.
Решение. а) Подстановка предельного значения аргумента 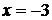 приводит к неопределенному выражению вида
приводит к неопределенному выражению вида 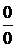 .
.
Для устранения этой неопределенности разложим числитель и знаменатель дроби на множители и сократим дробь на множитель 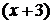 . Такое сокращение возможно, так как множитель
. Такое сокращение возможно, так как множитель 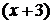 отличен от нуля при
отличен от нуля при 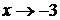 :
:
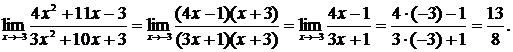
б) При  выражение
выражение 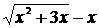 дает неопределенность вида
дает неопределенность вида 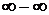 . Для ее устранения умножим и разделим это выражение на
. Для ее устранения умножим и разделим это выражение на 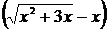 :
:
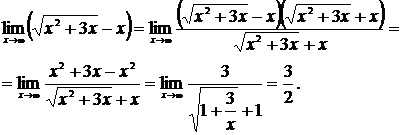
в) Обозначим 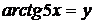 . Тогда
. Тогда 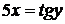 и
и 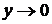 при
при 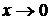 . Применяя свойства пределов и формулу первого замечательного предела
. Применяя свойства пределов и формулу первого замечательного предела 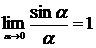 , имеем:
, имеем:
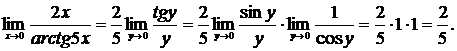
г) При 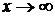 выражение
выражение 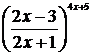 является неопределенностью вида
является неопределенностью вида 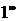 . Для устранения этой неопределенности представим основание степени в виде суммы 1 и бесконечно малой при
. Для устранения этой неопределенности представим основание степени в виде суммы 1 и бесконечно малой при 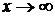 величины и применим формулу второго замечательного предела:
величины и применим формулу второго замечательного предела:
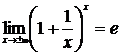 .
.
Тогда имеем:
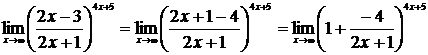 .
.
Пусть 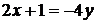 . Тогда
. Тогда 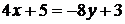 и
и 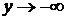 при
при 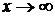 . Переходя к переменной у, получим:
. Переходя к переменной у, получим:
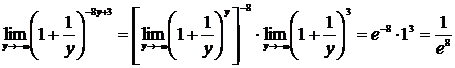 .
.
| Таблица производных | Таблица интегралов | ||||
1.  2.
2. 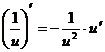 3.
3. 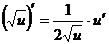 4.
4. 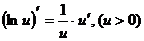 5.
5. 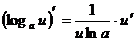 , , 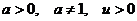 6.
6. 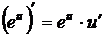 7.
7. 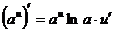 , , 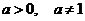 8.
8. 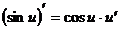 9.
9. 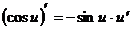 10.
10. 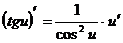 11.
11.  12.
12. 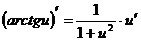 13.
13. 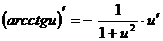 14.
14. 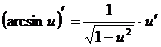 15.
15. 
| 1. 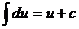 2.
2. 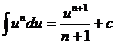 3.
3. 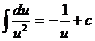 4.
4. 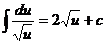 5.
5. 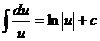 6.
6. 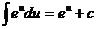 7.
7. 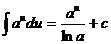 8.
8. 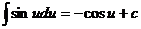 9.
9.  10.
10. 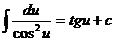 11.
11. 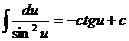 12.
12. 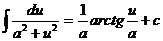 13.
13. 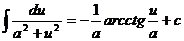 14.
14. 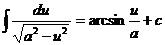 15.
15. 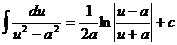 16.
16. 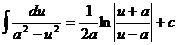 17.
17. 
|
Задача 2. Найдите производные функций:
а) 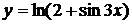 ; б)
; б) 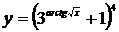 ; в)
; в) 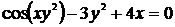 .
.
Решение. а) Последовательно применяя правило дифференцирования сложной функции, правила и формулы дифференцирования, имеем:
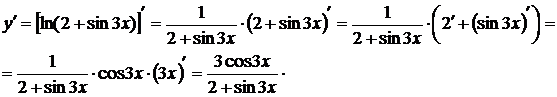
б)

в) В данном случае функциональная зависимость задана в неявном виде. Для нахождения производной 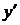 нужно продифференцировать по переменной х обе части уравнения, считая при этом у функцией от х, а затем полученное уравнение разрешить относительно
нужно продифференцировать по переменной х обе части уравнения, считая при этом у функцией от х, а затем полученное уравнение разрешить относительно 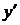 :
:
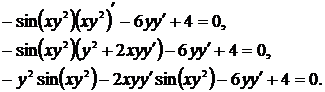
Из последнего уравнения находим 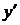 :
:
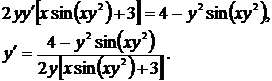
Задача 3. Исследовать функцию  и построить ее график.
и построить ее график.
Решение. Исследование функции проведем по следующей схеме:
1. Найдем область определения функции.
2. Исследуем функцию на непрерывность.
3. Установим, является ли функция четной, нечетной.
4. Найдем интервалы возрастания и убывания функции и точки экстремума.
5. Найдем интервалы выпуклости и вогнутости кривой и точки ее перегиба.
6. Найдем асимптоты кривой.
Реализуем указанную схему:
1. Функция определена при всех значениях аргумента х, кроме 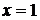 .
.
2. Данная функция является элементарной, поэтому она непрерывна на своей области определения, т. е. на интервалах 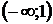 и
и 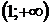 . В точке
. В точке 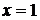 функция терпит разрыв второго рода.
функция терпит разрыв второго рода.
3. Для установления четности или нечетности функции проверим выполнимость равенств 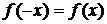 (тогда
(тогда 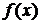 – четная функция) или
– четная функция) или 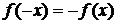 (для нечетной функции) для любых х и –х из области определения функции:
(для нечетной функции) для любых х и –х из области определения функции:
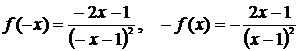 .
.
Следовательно, 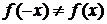 и
и 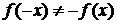 , то есть данная функция не является ни четной, ни нечетной.
, то есть данная функция не является ни четной, ни нечетной.
4. Для исследования функции на экстремум найдем ее первую производную:
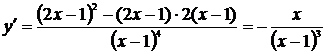 .
.
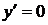 при
при 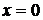 и
и 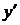 – не существует при
– не существует при 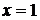 . Тем самым имеем две критические точки:
. Тем самым имеем две критические точки: 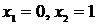 . Но точка
. Но точка 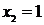 не принадлежит области определения функции, экстремума в ней быть не может.
не принадлежит области определения функции, экстремума в ней быть не может.
Разобьем числовую ось на три интервала (рис. 5): 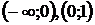 ,
, 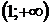 .
.
В первом и третьем интервалах первая производная отрицательна, следовательно, здесь функция убывает; во втором интервале – положительна и данная функция возрастает. При переходе через точку 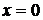 первая производная меняет свой знак с минуса на плюс, поэтому в этой точке функция имеет минимум:
первая производная меняет свой знак с минуса на плюс, поэтому в этой точке функция имеет минимум: 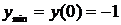 . Значит,
. Значит, 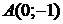 – точка минимума.
– точка минимума.

Нарис. 5 знаками +, – указаны интервалы знакопостоянства производной у', а стрелками – возрастание и убывание исследуемой функции.
5. Для определения точек перегиба графика функции и интервалов выпуклости и вогнутости кривой найдем вторую производную:
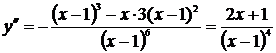 .
. 
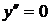 при
при  и
и 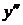 – не существует при
– не существует при 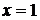 . Разобьем числовую ось на три интервала (рис. 6):
. Разобьем числовую ось на три интервала (рис. 6): 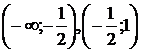 ,
, 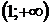 . На первом интервале вторая производная
. На первом интервале вторая производная 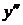 отрицательна и дуга исследуемой кривой выпукла; на втором и третьем интервалах
отрицательна и дуга исследуемой кривой выпукла; на втором и третьем интервалах 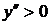 , тем самым график является вогнутым. При переходе через точку
, тем самым график является вогнутым. При переходе через точку 
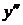 меняет свой знак, поэтому
меняет свой знак, поэтому  – абсцисса точки перегиба.
– абсцисса точки перегиба.
Следовательно, 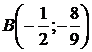 – точка перегиба графика функции.
– точка перегиба графика функции.
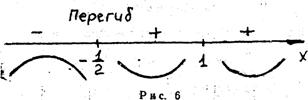
6. 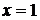 – точка разрыва функции, причем
– точка разрыва функции, причем 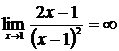 . Поэтому прямая
. Поэтому прямая 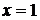 является вертикальной асимптотой графика. Для определения уравнения наклонной асимптоты
является вертикальной асимптотой графика. Для определения уравнения наклонной асимптоты 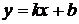 воспользуемся формулами:
воспользуемся формулами:
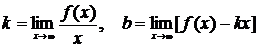 .
.
Тогда
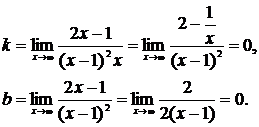
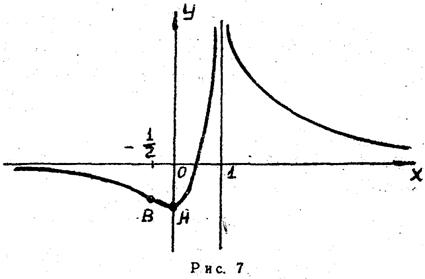
При вычислении последнего предела использовалось правило Лопиталя. Значит прямая 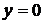 есть горизонтальная асимптота графика исследуемой функции, представленного на рис. 7.
есть горизонтальная асимптота графика исследуемой функции, представленного на рис. 7.
Задача 4. а) Найти 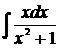 .
.
Решение. Применяя подстановку 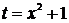 , приведем данный интеграл к табличному интегралу 2. Положим
, приведем данный интеграл к табличному интегралу 2. Положим 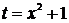 , тогда
, тогда 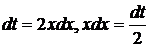 .
.
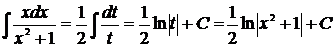 .
.
б) Найти 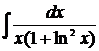 .
.
Применяя подстановку 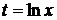 , приведем данный интеграл к формуле 10.
, приведем данный интеграл к формуле 10.
Положим 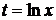 , тогда
, тогда 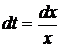 .
.
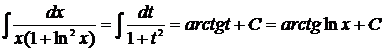 .
.
в) Найти 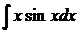 .
.
Принимаем 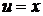 и
и 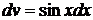 ; тогда
; тогда 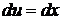 и
и 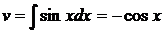 , следовательно
, следовательно 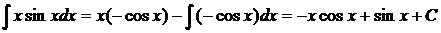 .
.
в2) Найти 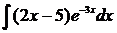 .
.
Принимаем 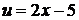 и
и 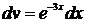 ; тогда
; тогда 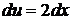 и
и 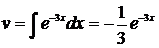 . Применяя формулу интегрирования по частям, будем иметь:
. Применяя формулу интегрирования по частям, будем иметь:
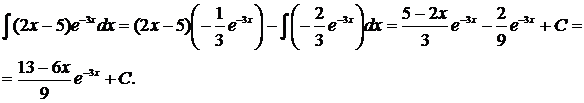
г) Найти  .
.
Принимаем 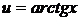 и
и 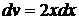 ; тогда
; тогда 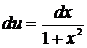 и
и 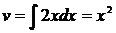 , следовательно,
, следовательно,
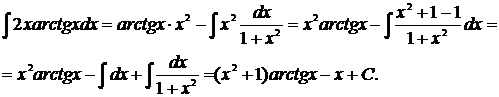
д) Найти интеграл 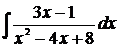 .
.
Преобразуем знаменатель дроби, стоящей под знаком интеграла, следующим образом:
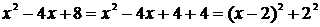 .
.
Тогда после подстановки 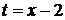 получаем
получаем
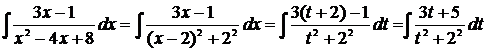 =
=

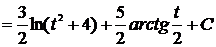 =
=
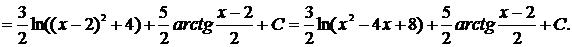
При этом при вычислении интеграла 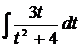 мы воспользовались заменой переменной
мы воспользовались заменой переменной  . Тогда
. Тогда 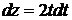 , откуда
, откуда
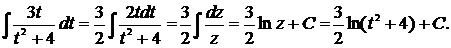
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|
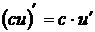 ,
2.
,
2. 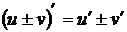 3.
3. 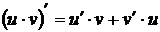 4.
4. 
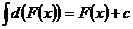 2.
2. 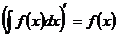 3.
3. 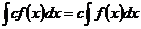 4.
4.