Рис. 7. Шаровое звёздное скопление — Википедия, Скопление M 53

Рис. 2

Сила взаимодействия между материальной точкой и сплошным шаром.

Непрерывно накладывая концентрические шаровые слои друг на друга, можно образовать сплошной шар, имеющий массу М и радиус R₀. Пользуясь уравнением (1), мы получим для точек, находящихся вне шара, следующую формулу, определяющую силу притяжения пробной массы в поле тяготения сплошного шара:

F = -	G m М	.	(2)
	r²

Напомним, что r – это расстояние пробной массы от центра шара (рис. 3).

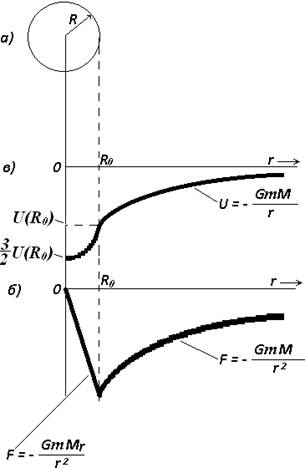
а) Однородный сплошной шар радиусом R₀ и массой М. б) Потенциальная энергия материальной точки m, находящейся на расстоянии r от центра сплошного шара радиусом R₀ и массой М. в) Сила, действующую материальную точку m. При r< R эта сила пропорциональна r.

Рис. 3

Этот основной результат можно было бы получить также и непосредтвенным интегрированием элементов силы по поверхности шарового слоя, но наш путь решения математически более краток. Обобщая уравнение (2), легко легко убедиться, что сила взаимодействия между двумя однородными шарами с массами М₁ и М₂ равна силе взаимодействия между двумя материальными точками с массами М₁ и М₂ , находящимися в центрах соответствующих шаров. Заменив один шар материальной точкой, мы можем затем заменить материальной точкой и второй шар. Этот вывод следует большой удачей, так как он позволяет упростить многие расчёты.

Сила взаимодействия между объектом (материальной точкой) и галактикой шаровой формы (сплошным шаром).

Допустим, на минутку, что в галактике шаровой формы имеет распределение плотности массы (звёзд) равномерно по всему объёму, т. е. сплошным шаром.

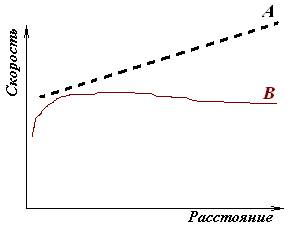
Рис. 4. Кривая вращения галактики шаровой формы равномерного распределения плотности: предсказанная ( A ) и наблюдаемая ( B )

Т. е. r - плотность, если распределение плотности равномерно, получается поделить массу галактики М на объём, радиуса R.

r =	3М		(3)
	4pR₀³

Т. к. М_r зависит от пропорциональности r³, если распределение плотности равномерно.

М(r) =	М	r³	(4)
	R₀³

Тогда справедливо, что при r< R формула будет иметь вид:

F(r) = -	G m М	r	(5)
	R₀³

Если же наблюдаемое распределение скоростей ( v = Const. ), то можно предположить, что зависимость М(r) будет пропорциональна r, т. е. распределение плотности пропорциональна 1/r², т. е.:

М(r) =		М	r	(6)
		R₀

	r(r) =	М		(7)
		4pR₀ r²

Тогда сила притяжения будет, в зависимости от расстояния, обратно пропорциональна r.

F(r) = -	G m М		(8)
	R₀ r

Где r(r) - плотность (для r £ R₀, ), М – масса галактики, R₀ - радиус галактики.

В этом случае, предсказанная ( A ) и наблюдаемая (В) распределение скоростей будут совпадать (почти), (см. Рис. 5)

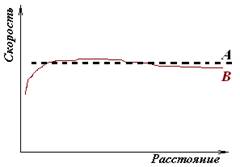
Рис. 5. Кривая вращения галактики шаровой формы неравномерного распределения плотности: предсказанная ( A ) и наблюдаемая ( B )

Задача о движения одного тела и Законы Кеплера в галактике шаровой формы.

Задача двух тел для однородных шаров или материальных точек была сведена о движении одного тела, задаваемой уравнении:

m	d²r	= -	G М₁ М_r	+ mw2r	(9)
	dt²		r²

Кроме того, можно указать и период вращения:

T²	=	4p²a³	(10)
		G (М₁ + М₂)

Очевидным свойством эллипса является равенство:

2a = r_max + r_min

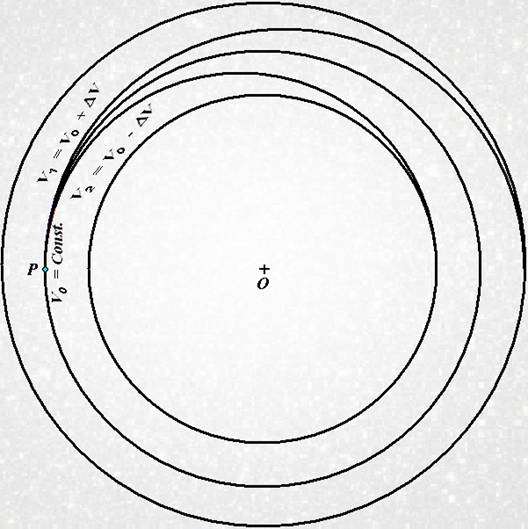
На этом рисунке изображено семейство траекторий материальной точки, притягиваемой к началу координат ([2], с. 310):

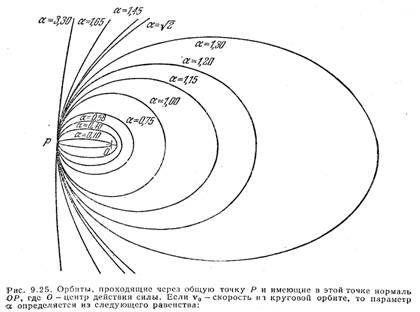
(Рис. 6)

(все эти уравнения (9) и (10), а также указанный рисунок, приводится в [2])

Однако, в галактике шаровой формы, семейство траекторий материальной точке получется всё по другому.

Указанную выше в галактике шаровой формы, имеющую распределение плотности массы (звёзд) пропорциональна 1/r², в формуле (2) можно указать, что m = М₁ (т. к. М₁ на очень меньше М₀), используя формулу (9) и сократив, получаем уравнение:

d²r	= -	G М	+	V²	(11)
dt²		R₀ r		r

Рис. 7. Шаровое звёздное скопление — Википедия, Скопление M 53

Т. е., распределение скоростей ( V = Const. ), то можно предположить, что зависимость М(r) будет пропорциональна r (ф. 6), т. е. распределение плотности пропорциональна 1/r²(ф. 7).

(Для того, чтобы изобразить орбиты на фоне шарового скопления, я " осветлил" фото с Википедии, сделав его достаточно бледным, чтоб орбиты были легко видны. )

⇐ Предыдущая 1 234 Следующая ⇒