Главная

Контакты

Случайная статья

• Автоматизация
• Антропология
• Археология
• Архитектура
• Биология
• Ботаника
• Бухгалтерия
• Военная наука
• Генетика
• География
• Геология
• Демография
• Деревообработка
• Журналистика
• Зоология
• Изобретательство
• Информатика
• Искусство
• История
• Кинематография
• Компьютеризация
• Косметика
• Кулинария
• Культура
• Лексикология
• Лингвистика
• Литература
• Логика
• Маркетинг
• Математика
• Материаловедение
• Медицина
• Менеджмент
• Металлургия
• Метрология
• Механика
• Музыка
• Науковедение
• Образование
• Охрана Труда
• Педагогика
• Полиграфия
• Политология
• Право
• Предпринимательство
• Приборостроение
• Программирование
• Производство
• Промышленность
• Психология
• Радиосвязь
• Религия
• Риторика
• Социология
• Спорт
• Стандартизация
• Статистика
• Строительство
• Технологии
• Торговля
• Транспорт
• Фармакология
• Физика
• Физиология
• Философия
• Финансы
• Химия
• Хозяйство
• Черчение
• Экология
• Экономика
• Электроника
• Электротехника
• Энергетика

ДЗ №3 Механика твёрдого тела.  Колебания и волны.

ДЗ №3 Механика твёрдого тела.  Колебания и волны.

Задачи

156.  Однородный диск радиусом R = 0, 2 м и мас­сой m = 5 кг вращается вокруг оси, проходящей че­рез его центр перпендикулярно к его плоскости. За­висимость угловой скорости w вращения диска от времени t дается уравнением

w = А + Bt², где В = 8 рад/с².

   Найти касательную силу F, приложенную к ободу диска. Трением в оси пренебречь.

157. Тонкостенный цилиндр, масса которого m = 12 кг, а диа­метр основания D = 30 см, вращается согласно уравнению

j = A + Bt + Ct³, где A = 4 рад, В = 2 рад/с, С = 0, 2 рад/с³.

  Определить действующий на цилиндр момент сил М в момент времени t = 3 с.

158. Стержень вращается вокруг оси, проходящей через его середину согласно уравнению

j = At + Bt³, где A = 2 рад/с, В = 0, 2 рад/с³.

   Определить вращающий момент М, действующий на стержень через

t = 2 с после начала вращения, если момент инерции стержня I = 0, 048 кг ^. м².

159. Маховик, момент инерции которого I = 63, 6 кг ^. м², вращается с угловой скоростью w = 31, 4 рад/с. Найти момент сил торможения М, под действием которого маховик останавливается через время t = 20 с. Маховик считать однородным диском.

160. К ободу колеса радиусом R = 0, 5 м и массой m = 50 кг приложена касательная сила F = 100 Н. Найти угловое ускорение e колеса. Через какое время t после начала действия силы колесо будет иметь частоту вращения n = 100 об/с?           Колесо счи­тать однородным диском. Трением пренебречь.

161. На обод маховика диаметром D = 60 см намотан шнур, к концу которого привязан груз массой m = 2 кг. Определить момент инерции I маховика, если он, вращаясь равноускоренно под дейст­вием силы тяжести груза, за время t = 3 с приобрел угловую ско­рость w = 9 рад/с.

162.  Шкив радиусом R = 0, 2 м и массой m = 10 кг соединен с мотором при помощи приводного ремня. Сила натяжения ремня, идущего без сколь­жения, F = 14, 7 Н. Какую частоту вращения n будет иметь шкив через время t = 10 с после начала движе­ния? Шкив считать однородным диском. Трением пре­небречь.

163. Маховое колесо, момент инерции которого I = 245 кг^. м² вращается с частотой     n = 20 об/с. Че­рез время t = 1 мин после того, как на колесо пере­стал действовать момент сил М, оно остановилось. Найти момент сил трения М_тр и число оборотов N, которое сделало колесо до полной остановки после прекращения действия сил. Колесо считать однород­ным диском.

164. Две гири с массами m₁ = 2 кг и m₂ = l кг соединены нитью, перекинутой       через блок массой m₃ = 1 кг. Найти ускорение, с которым движутся гири,        и силы натяжения F₁ и F₂ нитей, к которым подвешены гири. Блок считать         однородным диском. Трением пренебречь.

165. На барабан массой m₁ = 9 кг намотан шнур, к концу которого привязан груз массой m₂ = 2 кг. Найти ускорение груза. Барабан считать однород­ным цилиндром. Трением пренебречь.

166. На барабан радиусом R = 0, 5 м намотан шнур, к концу которого привязан груз массой m = 10 кг. Найти момент инерции I барабана, если из­вестно, что груз опускается с ускорением а = 2 м/с².

167. По плоской горизонтальной поверхности катится диск со скоростью 

v = 8 м/с. Определить коэффициент трения, если диск, будучи предоставленным самому себе, остановился, пройдя путь s = 18 м/с.

168. На барабан радиусом R = 20 см, момент инерции которого I = 0, 1 кг^. м² намотан шнур, к концу которого привязан груз массой m = 0, 5 кг. До начала вращения барабана высота груза над полом h = 1 м. Через какое время t груз опустится до пола? Найти кинетическую энергию Е_к груза в мо­мент удара о пол и силу натяжения нити F. Трением пренебречь.

169. Две гири с разными массами соединены нитью, перекинутой через блок, момент инерции которого I = 60 кг^. м² и радиус R = 20 см. Момент сил трения вращающегося блока М_тр = 100 Нм. Найти разность сил натяжения нити F₁ – F₂ по обе стороны блока, если известно, что блок вращается с угловым ускорением            e = 2, 36 рад/с². Блок считать однород­ным диском.

170. Определить момент силы M, который необходимо прило­жить к блоку, вращающемуся с частотой n = 12 с^-1, чтобы он оста­новился в течение времени           Dt = 8 с. Диаметр блока D = 30 см. Мас­су блока

m = 6 кг считать равномерно распределенной по ободу.

171. Блок, имеющий форму диска массой m = 0, 4 кг, вращается под действием натяжения нити, к концам которой подвешены грузы массами m₁ = 0, 3 кг и m₂ = 0, 7 кг. Определить силы натяжения нити F₁  и F₂ по обе стороны блока.

172. Нить с привязанными к ее концам грузами массой m₁ = 50 г и m₂ = 60 г перекинута через блок диаметром D = 4 см. Определить момент инерции I блока, если под действием силы тяжести грузов он получил угловое ускорение e = 1, 5 рад/с².

173. По касательной к шкиву маховика в виде диска диаметром D = 75 см и массой m = 40 кг приложена сила F = l кН. Определить угловое ускорение ε и частоту вращения n маховика через время t = 10 с после начала действия силы, если радиус r шкива равен 12 см. Силой трения пренебречь.

174. 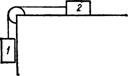Блок массой m = 1 кг укреплен на конце стола (рис. 12). Гири 1 и 2 одинако­вой массы m₁ = m₂ = 1 кг соединены нитью, переки­нутой через блок. Коэффициент трения гири 2 о стол m = 0, l. Найти ускорение, с которым движутся гири, и силы натяжения F₁ и F₂ нитей. Блок считать Рис. 12                 однородным диском. Трением в блоке пренебречь.

175. Шар диаметром R = 6 см и массой m = 0, 25 кг катится без скольжения по горизонтальной плоскости с частотой вращения n = 4 об/с. Найти кинетическую энергию Е_к шара.                                                                                         

176. Обруч и диск одинаковой массы m₁ = m₂  катятся без скольжения с одной и той же скоростью v. Кинетическая энергия обруча Е_к1 = 39, 2 Дж. Найти кинетическую энергию Е_к2 диска.

177. Шар массой m = 1 кг, катящийся без скольжения, ударяется о стенку и откатывается от нее. Скорость шара до удара о стенку v₁ = 10 см/с, после удара v₂ = 8 см/с. Найти количество теплоты Q, вы­делившееся при ударе шара о стенку.

178. Кинетическая энергия вала, вращающегося с частотой n = 5 об/с,  

Е_к = 60 Дж. Найти момент импульса L вала.

179. Мальчик катит обруч по горизонтальной до­роге со скоростью 

v = 7, 2 км/ч. На какое расстояние s может вкатиться обруч на горку за счет его кине­тической энергии? Уклон горки равен 10 м на каж­дые 100 м пути.

180. Определить скорости поступательного движения: а)шара, б)диска, в)обруча, скатившихся с наклонной плоскости высотой h = 20 см.

181. Колесо, вращаясь равнозамедленно, умень­шило за время t = 1 мин частоту вращения от n₁ = 300 об/мин до n₂ = 180 об/мин. Момент инерции колеса I = 2 кг ^. м². Найти угловое ускорение ε ко­леса, момент сил торможения М, работу А сил тор­можения и число оборотов N, сделанных колесом за время t = 1 мин.

182. Вентилятор вращается с частотой n = 900 об/мин. После выключения вентилятор, вра­щаясь равно замедленно, сделал до остановки N = 75 об. Работа сил торможения A = 44, 4 Дж. Най­ти момент инерции I вентилятора и момент сил тор­можения М.

183. Маховое колесо, момент инерции которого I = 245 кг^. м² вращается с частотой         n = 20 об/с. После того как на колесо перестал действовать вращающий момент, оно остановилось, сделав N = 1000 об. Найти момент сил трения М_тр и время t прошедшее от момента прекращения действия вра­щающего момента до остановки колеса.

184. По ободу шкива, насаженного на общую ось с маховым колесом, намотана нить, к концу которой подвешен груз массой m = 1 кг. На какое расстоя­ние          h должен опуститься груз, чтобы колесо со шки­вом получило частоту вращения n = 60 об/мин? Мо­мент инерции колеса со шкивом I = 0, 42 кг ^. м², ра­диус шкива R = 10 см.

185. Маховое колесо начинает вращаться с угло­вым ускорением e = 0, 5 рад/с² и через время t₁ = 16 с после начала движения приобретает момент импульса                 L = 73, 5 кг ^. м² / с. Найти кинетическую энергию Е_к колеса через время          t₂ = 20 с после начала движения.

186. Маховик вращается с частотой n = 10 об/с. Его кинетическая энергия           Е_к = 7, 85 кДж. За какое время t момент сил М_тр = 50 Нм, приложенный к              ма­ховику, увеличит угловую скорость w маховика вдвое?

187. К ободу диска массой m = 5 кг приложена касательная сила F = 20 H. Какую          кинетическую энергию Е_к будет иметь диск через время t = 5 с после начала действия силы?

188. Однородный стержень длиной L = 1 м подве­шен на горизонтальной оси, проходящей через верх­ний конец стержня. На какой угол a надо отклонить стержень, чтобы нижний конец стержня при прохож­дении положения равновесия имел скорость v = 5 м/с?

189. Горизонтальная платформа массой m₁ = 100 кг вращается вокруг вертикальной оси, про­ходящей через центр платформы, с частотой n₁ = 10 об/мин. Человек массой m₂ = 60 кг стоит при этом на краю платформы. С какой частотой n₂ начнет вращаться платформа, если человек пе­рейдет от края платформы к ее центру? Считать платформу однородным диском, а человека—точеч­ной массой. Какую работу А совершает человек при пе­реходе от края платформы к ее центру. Радиус платформы R = 1, 5 м.

190. Горизонтальная платформа массой m₁ = 80кг и радиусом R = 1 м вращается с частотой n₁ = 20 об/мин. В центре платформы стоит человек и держит в расставленных руках гири. С какой часто­той n₂  будет вращаться платформа, если человек, опустив руки, уменьшит свой момент инерции от I₁ = 2, 94 до               I₂ = 0, 98 кг^. м²? Считать платформу од­нородным диском. Во сколько раз увеличится кинетическая энергия Е_к платформы с человеком.

191. Человек массой m_o = 60 кг находится на не­подвижной платформе массой m = 100 кг. С какой частотой n будет вращаться платформа, если человек будет двигаться по окружности радиусом r = 5 м во­круг оси вращения? Скорость движения человека от­носительно платформы

v_отн = 4 км/ч. Радиус плат­формы R = 10 м. Считать платформу однородным диском, а человека точечной массой. Какова кинетическая энергия платформы.

192. Платформа, имеющая форму диска, может вращаться око­ло вертикальной оси. На краю платформы стоит человек массой m₁ = 60 кг. На какой угол j повернется платформа, если человек пойдет вдоль края платформы и, обойдя его, вернется в исходную точку на платформе? Масса m₂ платформы равна 240 кг. Момент инерции I человека рассчитывать как для материальной точки.

193. В центре скамьи Жуковского стоит человек и держит в руках стержень длиной l = 2, 4 м и массой m = 8 кг, расположенный вертикально по оси вращения скамейки. Скамья с человеком вра­щается с частотой n₁ = 1 с^-1. С какой частотой n₂ будет вращаться скамья с человеком, если он повернет стержень в горизонтальное положение? Суммарный момент инерции I человека и скамьи равен 6 кг^. м². Какую работу А совершает человек при повороте стержня.

194. Человек стоит на скамье Жуковского и держит в руках стержень, расположенный вертикально вдоль оси вращения ска­мейки. Стержень служит осью вращения колеса, расположенного на верхнем конце стержня. Скамья неподвижна, колесо вращается с частотой n = 10 с^-1. Радиус R колеса равен 20 см, его масса m = 3 кг. Определить частоту вращения n₂ скамьи, если человек повернет стержень на угол 180°? Суммарный момент инерции I человека и скамьи равен 6 кг^. м². Массу колеса можно считать рав­номерно распределенной по ободу.       Какую работу А совершает человек при повороте стержня.

195. Шарик массой m = 100 г, привязанный к концу нити длиной l₁ = 1 м, вращается, опираясь на горизонтальную плоскость, с ча­стотой n₁ = l с^-1. Нить укорачивается и шарик приближается к оси вращения до расстояния l₂ = 0, 5 м. С какой частотой n₂ будет при этом вращаться шарик? Какую работу А совершит внешняя сила, укорачивая нить? Трением шарика о плоскость пренебречь.

196. На краю платформы в виде диска, вращающегося по инер­ции вокруг вертикальной оси с частотой n₁ = 8 мин ^-1, стоит человек массой

m₁ = 70 кг. Когда человек перешел в центр платформы, она стала вращаться с частотой n₂ = 10 мин ^-1. Определить массу m₂ плат­формы. Момент инерции человека рассчитывать как для материальной точки. Какую работу совершает человек при пе­реходе от края платформы к ее центру. Радиус платформы R = 1, 5 м.

197. На краю неподвижной скамьи Жуковского диаметром D = 0, 8 м и массой         m₁ = 6 кг стоит человек массой m₂ = 60 кг. С какой угловой скоростью w начнет вращаться скамья, если человек поймает летящий на него мяч массой m = 0, 5 кг? Траектория мяча го­ризонтальна и проходит на расстоянии r = 0, 4 м от оси скамьи. Ско­рость мяча

v = 5 м/с. Найти кинетическую энергию скамьи.

198. Человек стоит на скамье Жуковского и держит в руках стержень вертикально вдоль оси вращения скамьи. Стержень слу­жит осью вращения колеса, расположенного на верхнем конце стер­жня. Скамейка неподвижна, колесо вращается с частотой n₁ = 15 с ^–1 . С какой угловой скоростью w₂ будет вращаться скамья, если человек повернет стержень на угол j = 180° и колесо окажется на ниж­нем конце стержня? Суммарный момент инерции человека и скамьи I = 8 кг ^. м², радиус колеса R = 25 см. Массу m = 2, 5 кг колеса можно считать равномерно распределенной по ободу. Считать, что центр масс человека с колесом находится на оси платформы. Какую работу А совершает человек при повороте стержня.

199. На скамье Жуковского стоит человек и держит в руках стержень вертикально по оси вращения скамьи. Скамья с человеком вращается с угловой скоростью w₁ = 4 рад/с. С какой угловой ско­ростью w₂ будет вращаться скамья с человеком, если повернуть стержень так, чтобы он занял горизонтальное положение? Суммар­ный момент инерции человека и скамьи I = 5 кг ^. м². Длина стержня         L = 1, 8 м, масса m = 6 кг. Считать, что центр масс стержня с человеком находится на оси платформы. Какую работу А совершает человек при повороте стержня.

200. Платформа в виде диска диаметром D = 3 м и массой m = 180 кг может вращаться вокруг вертикальной оси. С какой угло­вой скоростью w будет вращаться эта платформа, если по ее краю пойдет человек массой m₂ = 70 кг со скоростью v = 1, 8 м/с относи­тельно платформы? Найти кинетическую энергию платформы.

201. Платформа, имеющая форму диска, может вращаться около вертикальной оси. На краю платформы стоит человек. На какой угол j повернется платформа, если человек пойдет вдоль края плат­формы и, обойдя ее, вернется в исходную (на платформе) точку? Масса платформы m₁ = 280 кг, масса человека m₂ = 80 кг. Момент инерции человека рассчитывать как для материальной точки.