
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задача № 5. МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ. Механика
Задача № 5
Определить разность давлений ( Р1 - Р2 ) в широком (d1) и узком (d2) коленах горизонтальной трубы, если по трубе продувается воздух плотностью ρ =1, 29 кг/м3 со скоростью υ 1 в широком колене трубы.
| Заданные величины | номер варианта | |||||||||
| d1, см | ||||||||||
| d2, см | ||||||||||
| υ 1, м/с | ||||||||||
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
ПО ВЫПОЛНЕНИЮ ДОМАШНЕЙ РАБОТЫ:
Для решения задачи
- Необходимо переписать условие задачи.
- Записать условие с помощью принятых символов. Цифровые данные выписываются с обязательным указанием единиц измерения, выраженных в системе СИ.
3. Решение задачи должно быть пояснено (см. примеры).
- После решения выписать ответ (в СИ).
- Выбор варианта - по последней цифре зачетной книжки. Например: № зачетной книжки 1052, следовательно, вариант № 2
Механика
УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧИ № 1
Для решения задачи необходимо ознакомиться с разделом «Основы кинематики». Необходимо знать, что скорость есть первая производная по времени по отношению к пройденному пути, а ускорение есть вторая производная от S или первая производная по времени от скорости.
Пример решения задачи.
Уравнение движения материальной точки имеет вид S = Аt + Вt2, м. Определить для момента времени t = 1с. Пройденный телом путь, скорость и ускорение, если А = 2 м/с, В = 4 м/с2.
Решение:
| Дано: S = Аt + Вt2 t = 1 с А = 2 м/с В = 4 м/с2 | Решение: Для нахождения пройденного телом пути подставляем в уравнение движения начальные данные: S = Аt + Вt2 = 2*1 + 4*12=6 м. Для нахождения скорости берем первую производную от S по времени: V= S'=А+2Вt = 2+2*4*1=10 м/с Для нахождения ускорения берем первую производную от скорости по времени: а = V'=2В = 2*4 = 8 м/с2 |
| S -? V-? a-? | Ответ: S = 6 м, V=10 м/с, а =8 м/с2. |
УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧИ № 2
Для решения данной задачи необходимо знать второй закон Ньютона, уметь правильно расставить силы, действующие на тело, а также правильно записать проекции этих сил в выбранной системе координат. Необходимо также использовать зависимости S и V от времени в случае равноускоренного движения.
Пример решения задачи.
С вершины клина, длиною L= 2 м с углом наклона 30о начинает скользить небольшое тело. Коэффициент трения между телом и клином µ= 0, 1. Определить: скорость тела у основания клина.
 у
у
Дано:
L = 2 м
α = 30о
µ= 0, 1
 V -?
V -?
|      Решение: N Fтр Решение: N Fтр
   На тело действуют следующие силы: x На тело действуют следующие силы: x
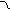 направленная вертикально вниз
сила тяжести mg, направленная mg
перпендикулярно опоре сила нормального
давления N и направленная против движения сила трения Fтр.
Скорость тела у основания клина можно определить по формуле:
V = Vo ± at. Для нахождения V надо знать ускорение а и времяt. Ускорение найдем, используя законы динамики и в частности 2 закон Ньютона. F = ma Выполняем проекции сил на выбранные оси Х и У
Х: ma = mg sin a - Fтр (1)
У: 0 = N - mg cos a (2)
Данная система уравнения решается подстановкой. Из (2) выражаем N
N = mg cos a (3)
Сила трения равна
F = µ N = µ mg cos a (4)
Далее решаем (1) подставляя (4)
ma = mg sin a - µ mg cos a
ma = mg (sin a - µ cos a )
Масса по разные стороны знака равно сокращается
a = g (sin a - µ cos a )
Далее подставляем значения и производим расчет:
а = 9, 81*(sin 30 - 0. 1*cos 30) = 4, 05 м/с2 направленная вертикально вниз
сила тяжести mg, направленная mg
перпендикулярно опоре сила нормального
давления N и направленная против движения сила трения Fтр.
Скорость тела у основания клина можно определить по формуле:
V = Vo ± at. Для нахождения V надо знать ускорение а и времяt. Ускорение найдем, используя законы динамики и в частности 2 закон Ньютона. F = ma Выполняем проекции сил на выбранные оси Х и У
Х: ma = mg sin a - Fтр (1)
У: 0 = N - mg cos a (2)
Данная система уравнения решается подстановкой. Из (2) выражаем N
N = mg cos a (3)
Сила трения равна
F = µ N = µ mg cos a (4)
Далее решаем (1) подставляя (4)
ma = mg sin a - µ mg cos a
ma = mg (sin a - µ cos a )
Масса по разные стороны знака равно сокращается
a = g (sin a - µ cos a )
Далее подставляем значения и производим расчет:
а = 9, 81*(sin 30 - 0. 1*cos 30) = 4, 05 м/с2
 Время можно найти из уравнения движения: Время можно найти из уравнения движения:
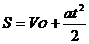 ,
где S = L, Vo=0. Тогда
t = ,
где S = L, Vo=0. Тогда
t = 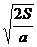 = = 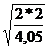 = 0. 99 c.
Используя полученные данные, определяем скорость тела.
V = at = 4. 05*0. 99 = 4 м/с = 0. 99 c.
Используя полученные данные, определяем скорость тела.
V = at = 4. 05*0. 99 = 4 м/с
|
| Ответ: V = 4 м/с |
УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧИ № 3
Для решения данной задачи необходимо использовать законы динамики движения и кинематику (см. решение предыдущей задачи).
Пример решения задачи:
Тело массой 5 кг поднимают с ускорением 2 м/с2 на расстояние 100 м по наклонной плоскости с углом наклона 15о. Коэффициент трения 0, 1. Определить работу, совершаемую при подъеме тела и мощность механизма.
| Дано: m = 5 кг а = 2 м/с2 S = 100 м а = 15о
А -? N -? | Решение:
 Работу, совершаемую при подъеме можно у Работу, совершаемую при подъеме можно у
 найти как произведение силы тяги
и перемещения по формуле N х найти как произведение силы тяги
и перемещения по формуле N х 
  А = Fт* S FT А = Fт* S FT
     Fтр
Силу тяги можно найти используя
законы динамики.
mg
х: ma = Fт - Fтр - mg sin a
у: 0 = N - mg cosa
решая совместно два уравнения и учитывая, что Fтр = µ N (см. задачу №2) получаем:
ma = Fт - µ mg cosa - mg sin a (1)
Выражаем из (1) силу тяги Fт
Fт = ma + µ mg cosa + mg sin a
Fт = m (a + µg cosa + g sin a) (2)
Поставляем в (2) значения параметров и находим силу тяги:
Fт = 5*(2+0, 1*9, 81*cos 15 + 9. 81*sin 15) = 27. 5 H (3)
Зная перемещение и силу тяги, найдем работу:
А = Fт* S = 27, 5 * 100 = 2750 Дж = 2, 75 кДж
Мощность механизма можно определить по формуле N=А/t.
Время подъема можно найти из кинематического уравнения движения: Fтр
Силу тяги можно найти используя
законы динамики.
mg
х: ma = Fт - Fтр - mg sin a
у: 0 = N - mg cosa
решая совместно два уравнения и учитывая, что Fтр = µ N (см. задачу №2) получаем:
ma = Fт - µ mg cosa - mg sin a (1)
Выражаем из (1) силу тяги Fт
Fт = ma + µ mg cosa + mg sin a
Fт = m (a + µg cosa + g sin a) (2)
Поставляем в (2) значения параметров и находим силу тяги:
Fт = 5*(2+0, 1*9, 81*cos 15 + 9. 81*sin 15) = 27. 5 H (3)
Зная перемещение и силу тяги, найдем работу:
А = Fт* S = 27, 5 * 100 = 2750 Дж = 2, 75 кДж
Мощность механизма можно определить по формуле N=А/t.
Время подъема можно найти из кинематического уравнения движения:
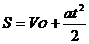 , отсюдаt = , отсюдаt = 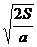 = = 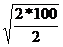 = 10с, тогда
N = 2750/10=275 Вт = 10с, тогда
N = 2750/10=275 Вт
|
| Ответ: А = 2, 75 кДж; N = 275 Вт. |
УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧИ № 4
Для решения задачи необходимо знать теорему Штейнера, которая позволяет определить момент инерции тела, вращающегося вокруг оси, не совпадающей с осью симметрии.
Таб. 1 Момент инерции некоторых тел при вращении вокруг оси симметрии.
| Тело | Момент инерции Jc |
| Полый тонкостенный цилиндр или кольцо | Jc = mR2 |
| Сплошной цилиндр или диск | Jc = 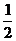 mR2 mR2
|
| Шар | Jc = 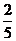 mR2 mR2
|
| Стержень (l - длина стержня) | Jc = 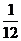 ml2 ml2
|
Пример решения задачи:
Кольцо радиусом R = 50 см и массой 300 г вращается вокруг оси проходящей через середину радиуса. Найти момент инерции кольца.
| Дано: R = 50 см = 0, 5 м m = 300 г = 0, 3 кг
J -? | Решение: а
    1- ось симметрии
2 - ось вращения R 1- ось симметрии
2 - ось вращения R
 а - расстояние между осями
По теореме Штейнера момент инерции
определяется следующим образом 1 2
J = Jc + ma2,
где Jc - момент инерции тела при вращении вокруг оси симметрии (см. таблицу 1)
J = mR2 + ma2 = m(R2 + a2 ) = 0. 3(0. 52+0. 252) = 0. 094 кг*м2 а - расстояние между осями
По теореме Штейнера момент инерции
определяется следующим образом 1 2
J = Jc + ma2,
где Jc - момент инерции тела при вращении вокруг оси симметрии (см. таблицу 1)
J = mR2 + ma2 = m(R2 + a2 ) = 0. 3(0. 52+0. 252) = 0. 094 кг*м2
|
| Ответ: J = 0. 094 кг*м2 |
УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧИ № 5
Для решения задач из данного раздела необходимо ознакомится с механикой жидкостей.
Пример решения задачи:
По трубе площадью поперечного сечения 50 см2 в широком колене и 20 см2 в узком течет вода со скоростью υ 1 = 10 м/с. Статическое давление в широком колене трубы Р1 =400 кПа. Определить давление в узком колене трубы. Плотность воды 1 г/см3.
| Дано: S1 = 50 см2=5*10-3 м2 S2 = 20 см2=2*10-3 м2 ρ = 1 г/см3 = 1000 кг/м3 υ 1 = 10 м/с Р1 = 400 кПа = 4*105Па
Р2 -? | Решение:
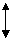      Статическое давление в
Статическое давление в
 узком колене трубы найдем S1 υ 1 υ 2 узком колене трубы найдем S1 υ 1 υ 2
 из уравнения Бернулли: S2 из уравнения Бернулли: S2
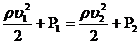 (1)
Из (1) выражаем Р2 (1)
Из (1) выражаем Р2
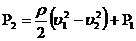 (2)
Скорость в узком колене трубы можно найти из уравнения неразрывности: S1 υ 1 = S2 υ 2
υ 2 = (2)
Скорость в узком колене трубы можно найти из уравнения неразрывности: S1 υ 1 = S2 υ 2
υ 2 =  = 5*10-3*10/2*10-3 = 25 м/с
Подставляем данные в (2)
Р2 = = 5*10-3*10/2*10-3 = 25 м/с
Подставляем данные в (2)
Р2 = 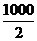 ( 102 - 252 ) +4*105 = 137500 Па = 137, 5 кПа ( 102 - 252 ) +4*105 = 137500 Па = 137, 5 кПа

|
| Ответ: Р2 = 137, 5 кПа |
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|
 µ = 0, 1
µ = 0, 1 а = R/2 = 0. 25 м
а = R/2 = 0. 25 м