
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
КОЭФФИЦИЕНТЫ
1.
1. Найдите значение выражения 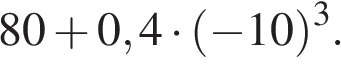
2. В таблице приведены расстояния от Солнца до четырёх планет Солнечной системы. Какая из этих планет ближе всех к Солнцу?
| Планета | Уран | Нептун | Марс | Венера |
| Расстояние (в км) | 2, 871 · 109 | 4, 497 · 109 | 2, 28 · 108 | 1, 082 · 108 |
1) Уран
2) Нептун
3) Марс
4) Венера
3. На координатной прямой точками отмечены числа 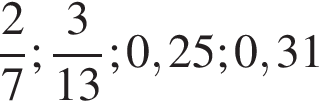
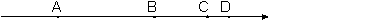
Какому числу соответствует точка D?
1) 
2) 
3) 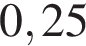
4) 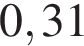
4. Какое из данных ниже чисел является значением выражения 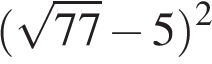
1) 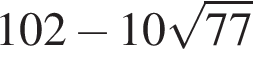
2) 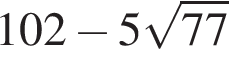
3) 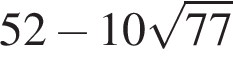
4) 
5. На графике изображена зависимость атмосферного давления от высоты над уровнем моря. На горизонтальной оси отмечена высота над уровнем моря в километрах, на вертикальной — давление в миллиметрах ртутного столба. Определите по графику, на какой высоте атмосферное давление равно 260 миллиметрам ртутного столба. Ответ дайте в километрах.
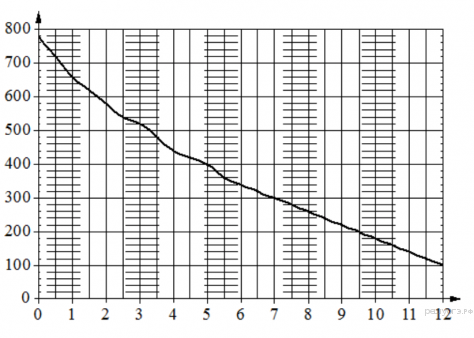
6. Найдите корни уравнения 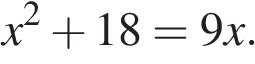
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
7. Магазин детских товаров закупает погремушку по оптовой цене 260 рублей за одну штуку и продаёт с 40-процентной наценкой. Сколько будут стоить 3 такие погремушки, купленные в этом магазине?
8. На диаграмме показано количество SMS, присланных слушателями за каждый час четырёхчасового эфира программы по заявкам на радио. Определите, на сколько больше сообщений было прислано за первые два часа программы по сравнению с последними двумя часами этой программы.
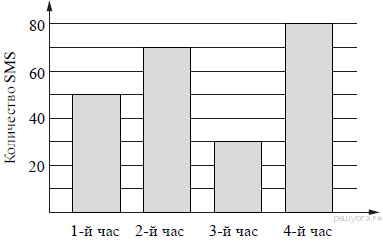
9. На экзамене по геометрии школьнику достаётся одна задача из сборника. Вероятность того, что эта задача по теме «Углы», равна 0, 35. Вероятность того, что это окажется задача по теме «Окружность», равна 0, 45. В сборнике нет задач, которые одновременно относятся к этим двум темам. Найдите вероятность того, что на экзамене школьнику достанется задача по одной из этих двух тем.
10. На рисунке изображены графики функций вида y = ax2 + c. Установите соответствие между графиками и знаками коэффициентов a и c.
ГРАФИКИ
А) 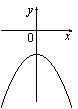
| Б) 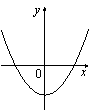
| В) 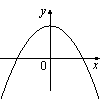
| Г) 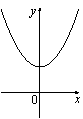
|
ЗНАКИ КОЭФФИЦИЕНТОВ
| 1) a > 0, c < 0 | 2) a < 0, c > 0 | 3) a > 0, c > 0 | 4) a < 0, c < 0 |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| А | Б | В | Г |
11. Арифметическая прогрессия задана условиями: 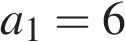 ,
,  . Какое из данных чисел является членом этой прогрессии?
. Какое из данных чисел является членом этой прогрессии?
| 1) 80 | 2) 56 | 3) 48 | 4) 32 |
12. Найдите значение выражения  при
при 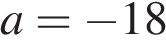 и
и 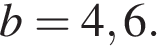
13. Период колебания математического маятника 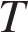 (в секундах) приближенно можно вычислить по формуле
(в секундах) приближенно можно вычислить по формуле 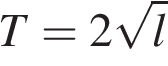 , где
, где 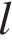 — длина нити (в метрах). Пользуясь этой формулой, найдите длину нити маятника (в метрах), период колебаний которого составляет 3 секунды.
— длина нити (в метрах). Пользуясь этой формулой, найдите длину нити маятника (в метрах), период колебаний которого составляет 3 секунды.
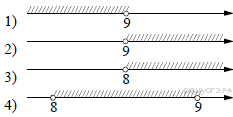
14. На каком рисунке изображено множество решений системы неравенств 
В ответе укажите номер правильного варианта.
15. 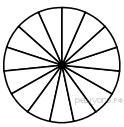 Колесо имеет 15 спиц. Углы между соседними спицами равны. Найдите величину угла (в градусах), который образуют две соседние спицы.
Колесо имеет 15 спиц. Углы между соседними спицами равны. Найдите величину угла (в градусах), который образуют две соседние спицы.
16. 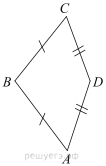
В выпуклом четырехугольнике ABCD известно, что  ,
,  ,
, 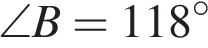 ,
,  . Найдите угол A. Ответ дайте в градусах.
. Найдите угол A. Ответ дайте в градусах.
17. 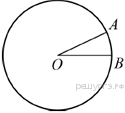 На окружности с центром O отмечены точки A и B так, что
На окружности с центром O отмечены точки A и B так, что 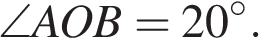 Длина меньшей дуги AB равна 88. Найдите длину большей дуги.
Длина меньшей дуги AB равна 88. Найдите длину большей дуги.
18. 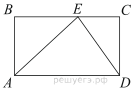
На стороне BC прямоугольника ABCD, у которого AB = 56 и AD = 89, отмечена точка E так, что ∠ EAB = 45°. Найдите ED.
19. 
На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.
20. Укажите номера верных утверждений.
1) Диаметр делит окружность на две равные дуги.
2) Параллелограмм имеет две оси симметрии.
3) Площадь треугольника равна его основанию, умноженному на высоту.
21. Решите уравнение 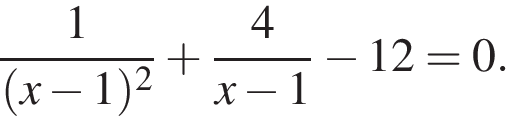
22. Теплоход проходит по течению реки до пункта назначения 76 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 3 км/ч, стоянка длится 1 час, а в пункт отправления теплоход возвращается через 20 часов после отплытия из него.
23. Постройте график функции 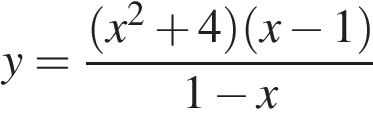 и определите, при каких значениях k прямая y = kx имеет с графиком ровно одну общую точку.
и определите, при каких значениях k прямая y = kx имеет с графиком ровно одну общую точку.
24. Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 12, а одна из диагоналей ромба равна 48. Найдите углы ромба.
25. В параллелограмме ABCD проведены высоты BH и BE к сторонам AD и CD соответственно, при этом BH = BE. Докажите, что ABCD — ромб.
26. Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 39, тангенс угла BAC равен  Найдите радиус окружности, вписанной в треугольник ABC.
Найдите радиус окружности, вписанной в треугольник ABC.
2. 1. Найдите значение выражения 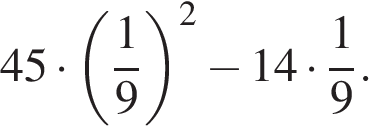
2. В таблице даны рекомендуемые суточные нормы потребления (в г/сутки) жиров, белков и углеводов детьми от 1 года до 14 лет и взрослыми.
| Вещество | Дети от 1 года до 14 лет | Мужчины | Женщины |
| Жиры | 40− 97 | 70− 154 | 60− 102 |
| Белки | 36− 87 | 65− 117 | 58− 87 |
| Углеводы | 170− 420 | 257− 586 | |
Какой вывод о суточном потреблении жиров 10-летней девочкой можно сделать, если по подсчётам диетолога в среднем за сутки она потребляет 102 г жиров?
В ответе укажите номер правильного варианта.
1) Потребление в норме.
2) Потребление выше рекомендуемой нормы.
3) Потребление ниже рекомендуемой нормы.
4) В таблице недостаточно данных.
3. На координатной прямой отмечены числа a и b. Какое из следующих утверждений неверно?
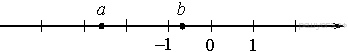
1) 
2) 
3) 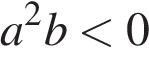
4) 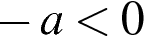
4. Значение какого из данных выражений является наибольшим?
1) 
2) 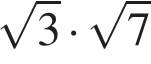
3) 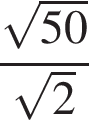
4) 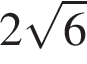
5. На графике показано изменение температуры воздуха на протяжении трёх суток. По горизонтали указывается дата и время, по вертикали — значение температуры в градусах Цельсия. Определите по графику наименьшую температуру воздуха 18 февраля. Ответ дайте в градусах Цельсия.
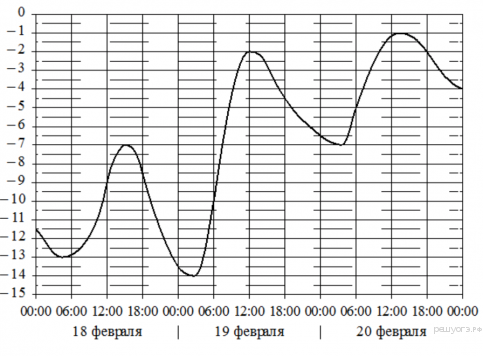
6. Решите уравнение 10x2 − 17x + 34 = 7x2 − 26x + 28.
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
7.
В начале учебного года в школе было 1250 учащихся, а к концу года их стало 950. На сколько процентов уменьшилось за год число учащихся?
8. На диаграмме показано распределение земель Уральского, Приволжского, Южного и Дальневосточного Федеральных округов по категориям. Определите по диаграмме, в каком округе доля земель сельскохозяйственного назначения наименьшая.
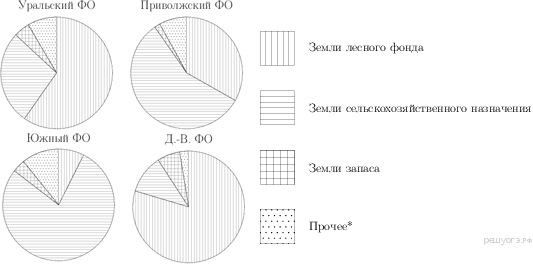
*прочее — это земли поселений; земли промышленности и иного специального назначения; земли особо охраняемых территорий и объектов.
1) Уральский ФО
2) Приволжский ФО
3) Южный ФО
4) Дальневосточный ФО
9. Стас выбирает трёхзначное число. Найдите вероятность того, что оно делится на 48.
10. 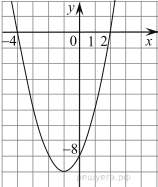
На рисунке изображён график квадратичной функции y = f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) Функция убывает на промежутке [− 1; +∞ ).
2) f(− 3)< f(0).
3) f(x)< 0 при − 4< x< 2.
11. Арифметическая прогрессия задана условиями: 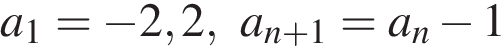 . Найдите сумму первых 9 её членов.
. Найдите сумму первых 9 её членов.
12. Найдите значение выражения 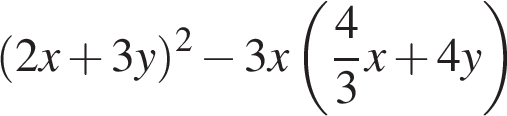 при
при 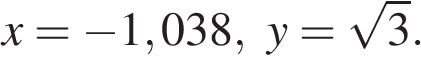
13. Расстояние s (в метрах) до места удара молнии можно приближённо вычислить по формуле s = 330t, где t — количество секунд, прошедших между вспышкой молнии и ударом грома. Определите, на каком расстоянии от места удара молнии находится наблюдатель, если t = 14 с. Ответ дайте в километрах, округлив его до целых.
14. Укажите неравенство, которое не имеет решений.
В ответе укажите номер правильного варианта.
1) x2 − 64 ≤ 0
2) x2 + 64 ≥ 0
3) x2 − 64 ≥ 0
4) x2 + 64 ≤ 0
15. Найдите периметр прямоугольного участка земли, площадь которого равна 800 м2 и одна сторона в 2 раза больше другой. Ответ дайте в метрах.
16. Два угла вписанного в окружность четырехугольника равны 82° и 58°. Найдите больший из оставшихся углов. Ответ дайте в градусах.
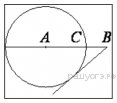
17. На отрезке 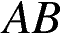 выбрана точка
выбрана точка  так, что
так, что  и
и  . Построена окружность с центром
. Построена окружность с центром 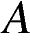 , проходящая через
, проходящая через  . Найдите длину отрезка касательной, проведённой из точки
. Найдите длину отрезка касательной, проведённой из точки 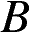 к этой окружности.
к этой окружности.
18. 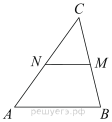 В треугольнике ABC отмечены середины M и N сторон BC и ACсоответственно. Площадь треугольника CNM равна 12. Найдите площадь четырёхугольника ABMN.
В треугольнике ABC отмечены середины M и N сторон BC и ACсоответственно. Площадь треугольника CNM равна 12. Найдите площадь четырёхугольника ABMN.
19. 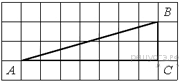 Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
20. Какие из следующих утверждений верны?
1) Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники подобны.
2) В равнобедренном треугольнике имеется не менее двух равных углов.
3) Площадь трапеции не превосходит произведения средней линии на высоту.
4) Если расстояние от точки до прямой меньше 1, то и длина любой наклонной, проведенной из данной точки к прямой, меньше 1.
21. Решите уравнение (x − 2)(x − 4)(x − 6) = (x − 2)(x − 3)(x − 6).
22. Баржа прошла по течению реки 48 км и, повернув обратно, прошла ещё 36 км, затратив на весь путь 6 часов. Найдите собственную скорость баржи, если скорость течения реки равна 5 км/ч.
23. Постройте график функции 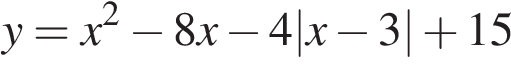 и найдите значения
и найдите значения  , при которых прямая
, при которых прямая  имеет с ним ровно три общие точки.
имеет с ним ровно три общие точки.
24. Окружность, вписанная в треугольник ABC , касается его сторон в точках M, K и P. Найдите углы треугольника ABC, если углы треугольника MKP равны 49°, 69° и 62°.
25. В параллелограмме 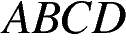 точка
точка  — середина стороны
— середина стороны 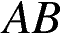 . Известно, что
. Известно, что  . Докажите, что данный параллелограмм — прямоугольник.
. Докажите, что данный параллелограмм — прямоугольник.
26. В треугольнике ABC известны длины сторон AB = 36, AC = 48, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону ACв точке D. Найдите CD.
3. 1. Найдите значение выражения: 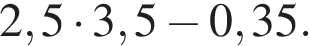
2. В таблице даны результаты олимпиад по географии и биологии в 8 «А» классе.
| Номер ученика | Балл по географии | Балл по биологии |
Похвальные грамоты дают тем школьникам, у кого суммарный балл по двум олимпиадам больше 120 или хотя бы по одному предмету набрано не меньше 65 баллов.
Сколько человек из 8 «А», набравших меньше 65 баллов по географии, получат похвальные грамоты?
В ответе укажите номер правильного варианта.
1) 1
2) 3
3) 4
4) 2
3. На координатной прямой точками A, B, C и D отмечены числа 0, 508; 0, 85; -0, 05; 0, 058. Какой точкой изображается число 0, 058?
В ответе укажите номер правильного варианта.
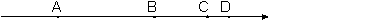
1) A
2) B
3) C
4) D
4. Между какими числами заключено число  ?
?
| 1) 38 и 40 | 2) 4 и 5 | 3) 77 и 79 | 4) 8 и 9 |
5. 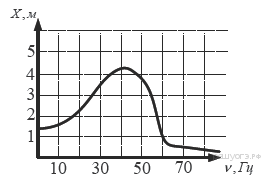 На рисунке изображен график зависимости амплитуды вынужденных колебаний от частоты колебаний. По вертикальной оси откладывается амплитуда (в м), по горизонтальной — частота колебаний (в Гц). По рисунку определите частоту колебаний, если амплитуда была равна 1 м.
На рисунке изображен график зависимости амплитуды вынужденных колебаний от частоты колебаний. По вертикальной оси откладывается амплитуда (в м), по горизонтальной — частота колебаний (в Гц). По рисунку определите частоту колебаний, если амплитуда была равна 1 м.
6. Решите уравнение 
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
7. Поступивший в продажу в январе мобильный телефон стоил 2400 рублей. В ноябре он стал стоить 1200 рублей. На сколько процентов снизилась цена на мобильный телефон в период с января по ноябрь?
8. 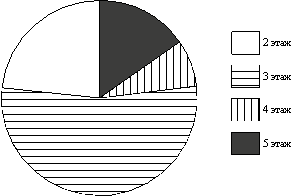 Участников конференции разместили в гостинице в одноместных номерах, расположенных на этажах со второго по пятый. Количество номеров на этажах представлено на круговой диаграмме.
Участников конференции разместили в гостинице в одноместных номерах, расположенных на этажах со второго по пятый. Количество номеров на этажах представлено на круговой диаграмме.
Какое утверждение относительно расселения участников конференции верно, если в гостинице разместились 50 участников конференции?
1) На четвёртом и пятом этажах разместилось одинаковое количество участников конференции.
2) Больше  всех участиников разместились на этажах выше второго.
всех участиников разместились на этажах выше второго.
3) Не менее 10 участников разместились на 4 этаже.
4) Не более четверти участников разместились на 2 этаже.
9. Игральную кость бросают дважды. Найдите вероятность того, что сумма двух выпавших чисел равна 6 или 9.
Результат округлите до сотых.
10. На рисунках изображены графики функций вида 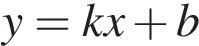 . Установите соответствие между знаками коэффициентов
. Установите соответствие между знаками коэффициентов 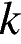 и
и 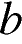 и графиками функций.
и графиками функций.
КОЭФФИЦИЕНТЫ
А) 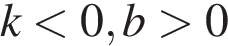
Б) 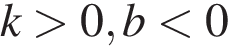
В) 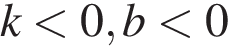
ГРАФИКИ
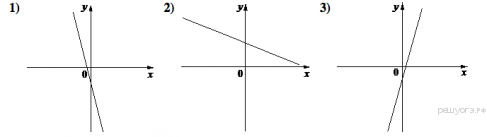
В таблице под каждой буквой укажите соответствующий номер.
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| A | Б | В |
11. Дана арифметическая прогрессия (an), разность которой равна 6, 8, a1 = − 3. Найдите a14.
12. Найдите значение выражения  при
при 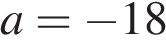 и
и 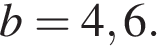
13. Чтобы перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, пользуются формулой tF = 1, 8tC + 32, где tC — температура в градусах Цельсия, tF — температура в градусах Фаренгейта. Скольким градусам по шкале Фаренгейта соответствует − 25 градусов по шкале Цельсия?
14. Решите неравенство 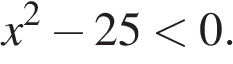
В ответе укажите номер правильного варианта.
1) (− ∞; +∞ )
2) нет решений
3) (− 5; 5)
4) (− ∞; − 5)∪ (5; +∞ )
15. 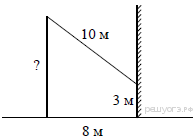 От столба к дому натянут провод длиной 10 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 8 м.
От столба к дому натянут провод длиной 10 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 8 м.
16. 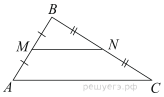
Точки 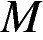 и
и 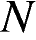 являются серединами сторон
являются серединами сторон 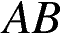 и
и 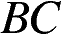 треугольника
треугольника 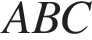 , сторона
, сторона 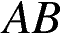 равна 26, сторона
равна 26, сторона 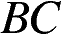 равна 39, сторона
равна 39, сторона  равна 48. Найдите
равна 48. Найдите 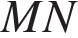
17.  К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 48, AO = 50.
К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 48, AO = 50.
18. 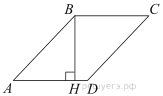
Высота 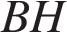 ромба
ромба 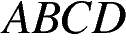 делит его сторону
делит его сторону  на отрезки
на отрезки  и
и  . Найдите площадь ромба.
. Найдите площадь ромба.
19. 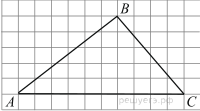
На клетчатой бумаге с размером клетки 1х1 изображён треугольник 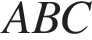 . Найдите длину его средней линии, параллельной стороне
. Найдите длину его средней линии, параллельной стороне  .
.
20. Какие из следующих утверждений верны?
1. Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.
2. Любой прямоугольник можно вписать в окружность.
3. Через заданную точку плоскости можно провести только одну прямую.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
21. Решите систему уравнений
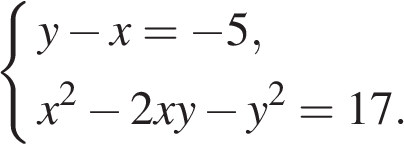
22. Игорь и Паша красят забор за 20 часов. Паша и Володя красят этот же забор за 24 часа, а Володя и Игорь — за 30 часов. За сколько часов мальчики покрасят забор, работая втроём?
23. При каких отрицательных значениях 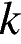 прямая
прямая 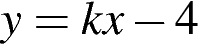 имеет с параболой
имеет с параболой  ровно одну общую точку? Найдите координаты этой точки и постройте данные графики в одной системе координат.
ровно одну общую точку? Найдите координаты этой точки и постройте данные графики в одной системе координат.
24. Точка H является основанием высоты BH, проведённой из вершины прямого угла Bпрямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH = 14.
25. Основания BC и AD трапеции ABCD равны соответственно 5 и 20, BD = 10. Докажите, что треугольники CBD и ADB подобны.
26. Основание AC равнобедренного треугольника ABC равно 18. Окружность радиуса 12 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|