
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Олімпіада з алгебри
«Хотелось бы чуть-чуть всемирной славы…»
Розв’язання задач
9 клас
1. Знайдіть усі функції 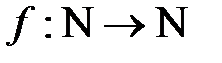 , для яких
, для яких 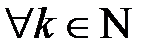 справджується умова:
справджується умова:
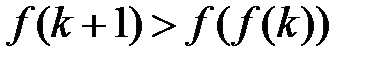 .
.
Відповідь: 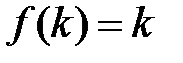 .
.
Розв’язання. Щоб довести, що наведена функція є єдиною можливою, достатньо показати, що 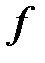 зростаюча. Тоді із зростання випливатиме, що
зростаюча. Тоді із зростання випливатиме, що
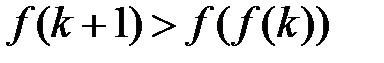
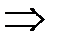
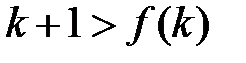
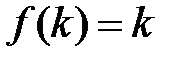 .
.
Розглянемо множину значень: 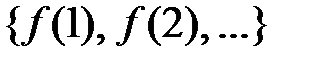 . За умовою задачі кожний член
. За умовою задачі кожний член 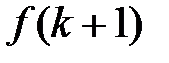 ,
, 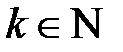 більше аналогічного члена
більше аналогічного члена 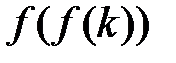 , за виключенням можливо
, за виключенням можливо 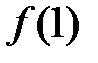 . Тому
. Тому 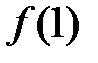 -- найменший член тієї множини.
-- найменший член тієї множини.
Розглянемо функцію 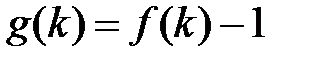 ,
, 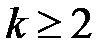 . Тоді в множині
. Тоді в множині 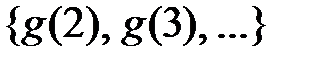 усі числа натуральні. Для
усі числа натуральні. Для 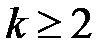 маємо, що
маємо, що
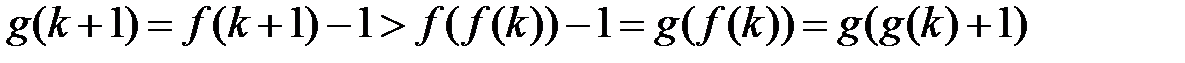 .
.
Це означає, що 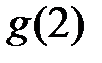 -- найменший елемент множини. Тоді
-- найменший елемент множини. Тоді 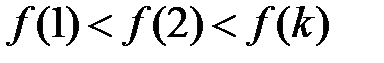
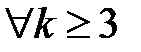 . Продовжуючи ці міркування, отримаємо, що
. Продовжуючи ці міркування, отримаємо, що  , що й завершує доведення.
, що й завершує доведення.
2. Нехай 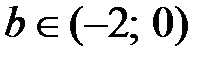 . Доведіть, що існує натуральне число
. Доведіть, що існує натуральне число 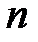 , для якого усі коефіцієнти многочлена
, для якого усі коефіцієнти многочлена 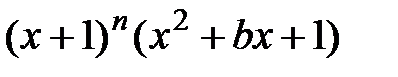 додатні.
додатні.
Розв’язання. Якщо розкрити дужки та звести подібні, то матимемо, що цей многочлен дорівнює
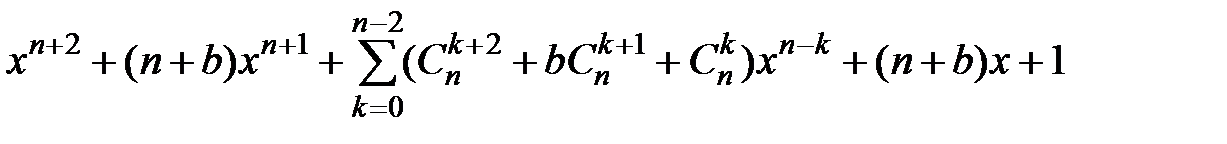 .
.
Очевидно, що при 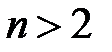 додатними мають бути коефіцієнти при доданках, що записані в сумі. Таким чином має справджуватись умова:
додатними мають бути коефіцієнти при доданках, що записані в сумі. Таким чином має справджуватись умова: 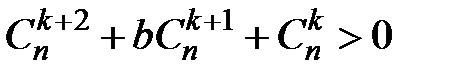
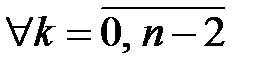 . Нехай
. Нехай 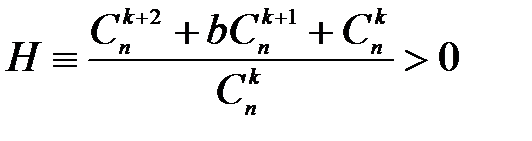 , тоді після спрощень матимемо, що
, тоді після спрощень матимемо, що
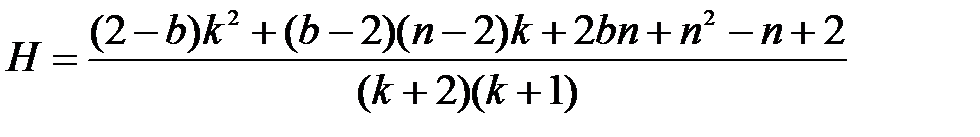 .
.
Чисельник цього виразу – квадратний тричлен відносно змінної 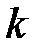 з додатним старшим коефіцієнтом та дискримінантом:
з додатним старшим коефіцієнтом та дискримінантом:
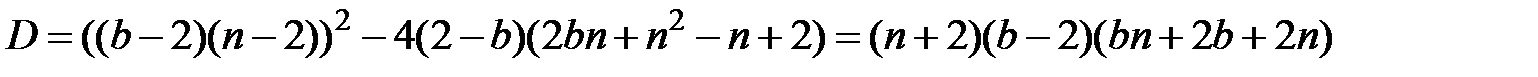 .
.
Оскільки 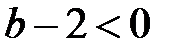 , то
, то 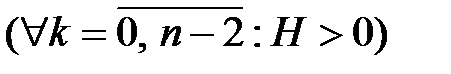



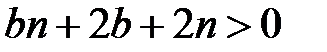

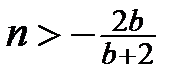 .
.
3. Натуральні числа 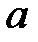 та
та 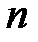 задовольняють рівність:
задовольняють рівність: 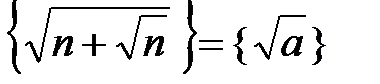 . Доведіть, що
. Доведіть, що 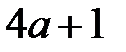 -- квадрат цілого числа.
-- квадрат цілого числа.
Розв’язання. Умову задачі можна переписати таким чином: 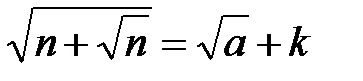 , де
, де 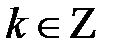 . Звідси випливає, що
. Звідси випливає, що 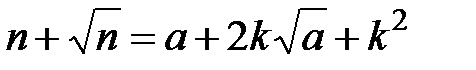 або
або 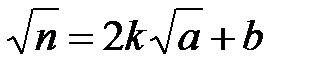 , де
, де 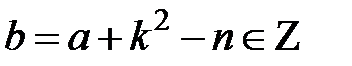 . Тоді
. Тоді 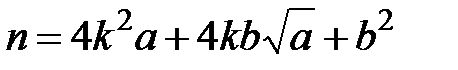
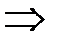
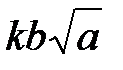 - раціональне. Якщо
- раціональне. Якщо 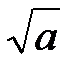 - раціональне, то
- раціональне, то 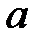 -- квадрат цілого числа. Але тоді й
-- квадрат цілого числа. Але тоді й 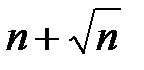 так само квадрат цілого числа, а тому й
так само квадрат цілого числа, а тому й 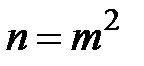 ,
, 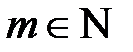 . Таким чином
. Таким чином 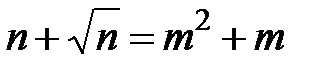 -- квадрат натурального числа, але оскільки
-- квадрат натурального числа, але оскільки
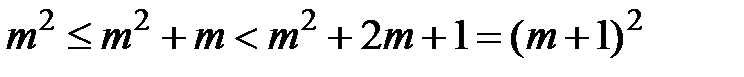 ,
,
то 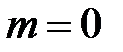 . Звідси
. Звідси 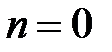 -- суперечність. Таким чином має бути
-- суперечність. Таким чином має бути 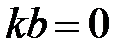 . Якщо
. Якщо 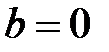 , то
, то 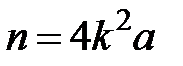 і одночасно
і одночасно 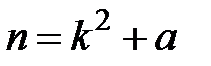 . Звідси
. Звідси 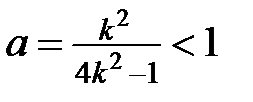 -- суперечність.
-- суперечність.
Заливається можливість 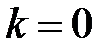 , тоді
, тоді 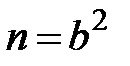 та
та 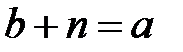 . Тоді
. Тоді 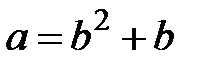 та
та 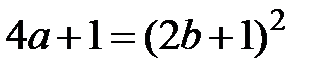 , що й треба було довести.
, що й треба було довести.
4. Для додатних чисел 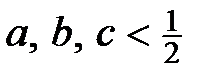 , що задовольняють умову
, що задовольняють умову 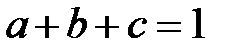 та для довільних дійсних чисел
та для довільних дійсних чисел 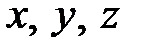 доведіть нерівність:
доведіть нерівність:
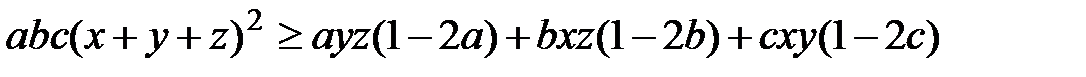 .
.
Розв’язання. З міркувань симетрії вважатимемо, що 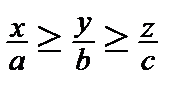 . Нехай
. Нехай 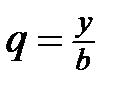 ,
, 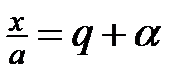 ,
, 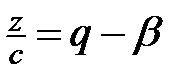 ,
, 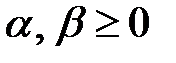 . Тоді
. Тоді 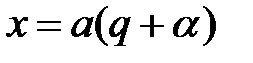 ,
, 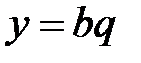 ,
, 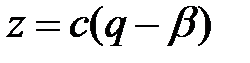 . Тоді нерівність можна переписати таким чином:
. Тоді нерівність можна переписати таким чином:
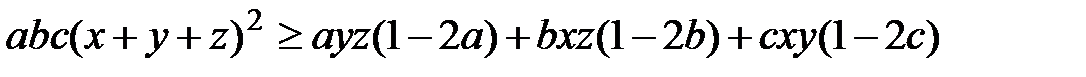

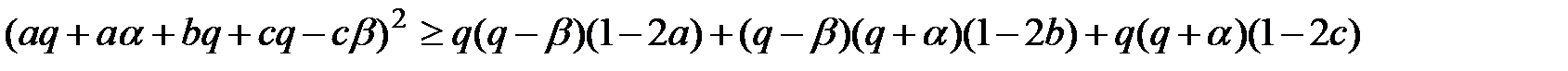

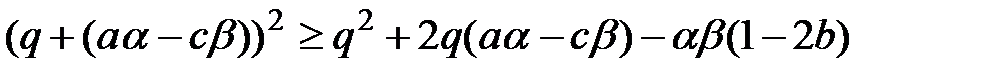

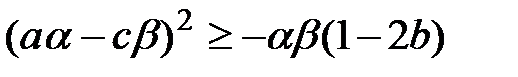 .
.
Остання нерівність справджується за умов задачі. Рівність тут можлива при 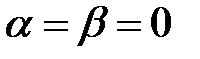 .
.
10 клас
1. Задача № 2 () за 9 клас.
2. Задача № 3 () за 9 клас.
3. Знайдіть усі функції 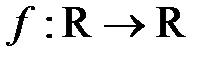 такі, що
такі, що 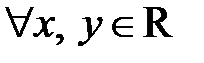 справджується рівність:
справджується рівність:
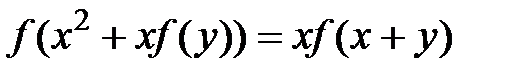 .
.
Відповідь: 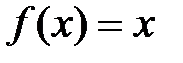 та
та 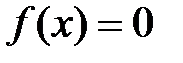 .
.
Розв’язання. Позначимо рівняння з умови через (1).
Покладемо в (1) 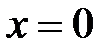 :
: 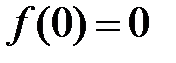 .
.
Покладемо в (1) 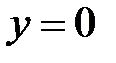 :
: 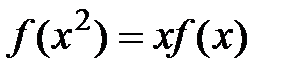 .
.
Припустимо, що існує 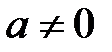 , для якого
, для якого 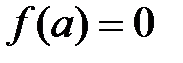 . Тоді
. Тоді
Покладемо в (1) 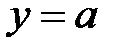 :
: 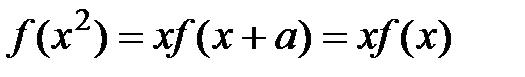
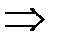
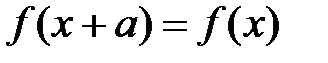 .
.
Припустимо, що 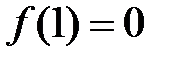 . Покладемо в (1)
. Покладемо в (1) 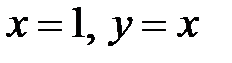 :
: 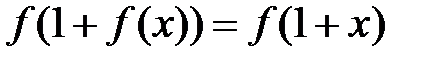 . Тоді з урахуванням умови
. Тоді з урахуванням умови 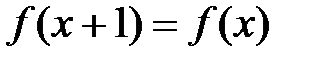 , то
, то 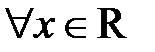 :
: 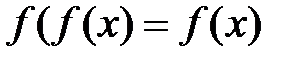 .
.
Нехай для деякого 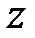
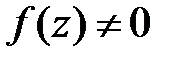 , то покладемо
, то покладемо 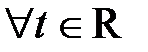
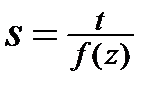
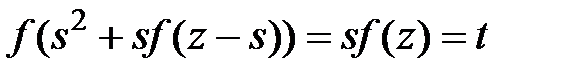 .
.
Таким чином 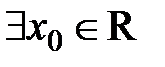 :
: 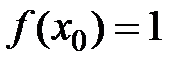
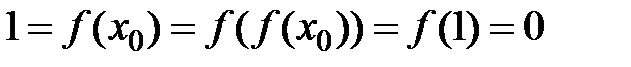 ,
,
одержали суперечність показує, що з умови 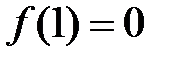 випливає, що
випливає, що 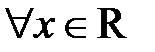
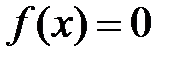 .
.
Нехай тепер 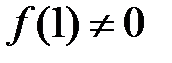 , тоді якщо існує
, тоді якщо існує 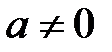 , для якого
, для якого 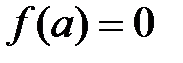 , то
, то 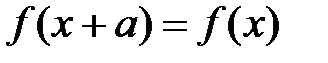 . Звідси
. Звідси
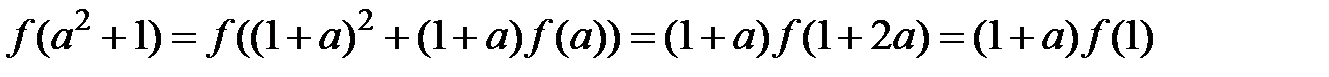 ,
,
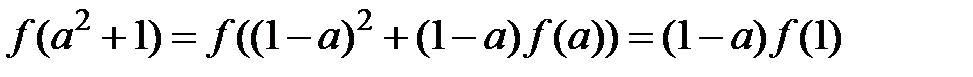
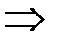
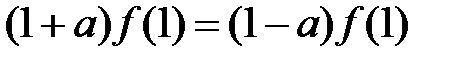
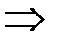
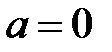 .
.
Звідси випливає, що з умови 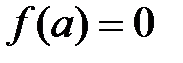 випливає, що
випливає, що 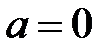 .
.
Покладемо в умові 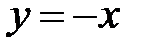 :
:
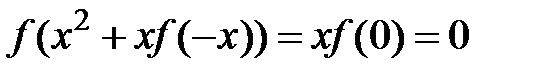
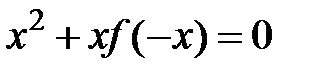
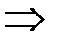
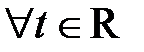
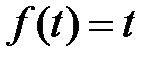 ,
,
що й завершує розв’язання.
4. Нехай 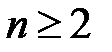 – натуральне число. Доведіть, що якщо дійсні числа
– натуральне число. Доведіть, що якщо дійсні числа 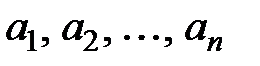 задовольняють умову
задовольняють умову 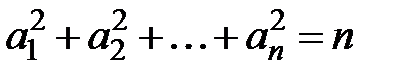 , то справджується нерівність:
, то справджується нерівність:
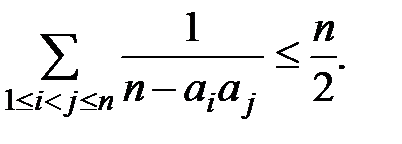
Розв’язання. Спочатку побачимо, що якщо 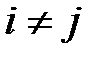 , тоді
, тоді 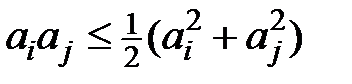 , тому
, тому
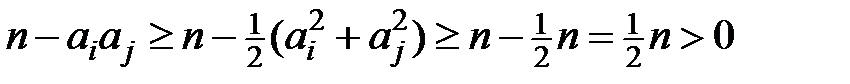 .
.
Позначимо через 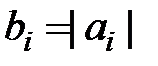 ,
, 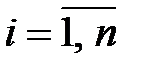 , то
, то 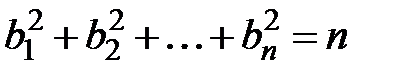 та
та 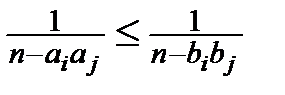 . Звідси випливає, що твердження задачі достатньо довести для випадку невід’ємних чисел
. Звідси випливає, що твердження задачі достатньо довести для випадку невід’ємних чисел 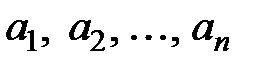 .
.
Множимо обидва боки 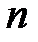 , матимемо:
, матимемо:
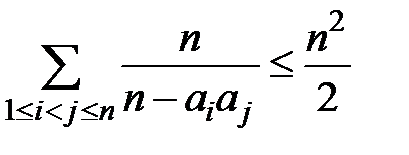 .
.
Оскільки 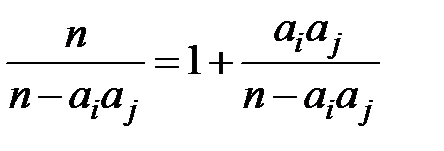 , то треба довести таку нерівність:
, то треба довести таку нерівність:
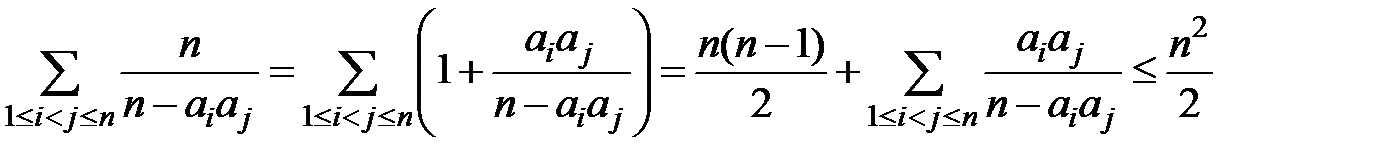
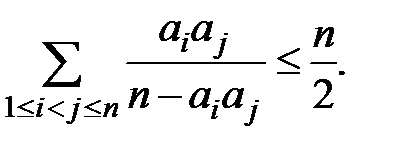 (1)
(1)
Якщо для деякого 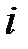 маємо
маємо 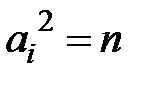 , то
, то 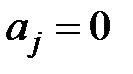
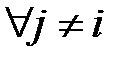 і нерівність (1) – очевидна. Тепер розглянемо випадок
і нерівність (1) – очевидна. Тепер розглянемо випадок 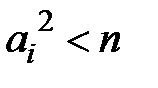
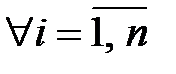 . Нехай далі
. Нехай далі 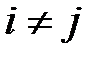 . Оскільки
. Оскільки
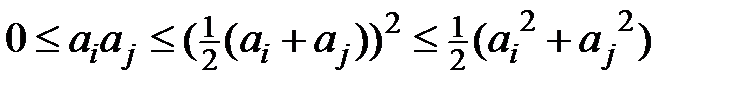 , то
, то
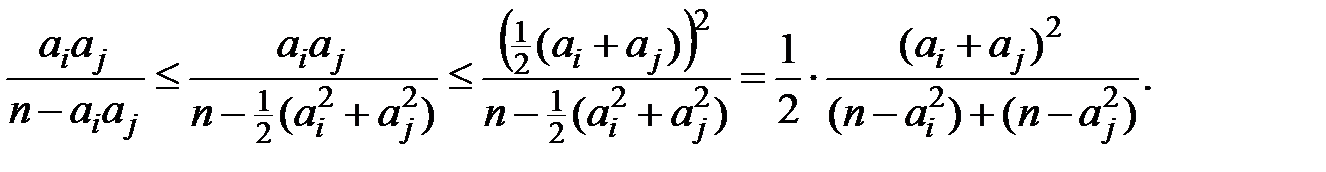 (2)
(2)
Оскільки 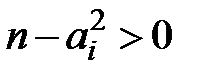 , то з нерівності Шварца маємо:
, то з нерівності Шварца маємо:
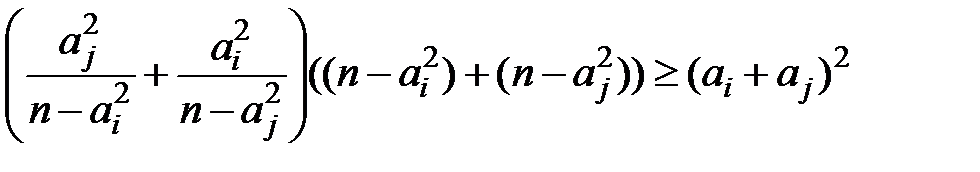
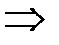
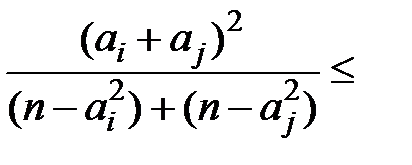
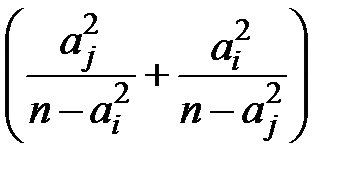 (3)
(3)
Поєднуючи нерівності (2) та (3), отримаємо:
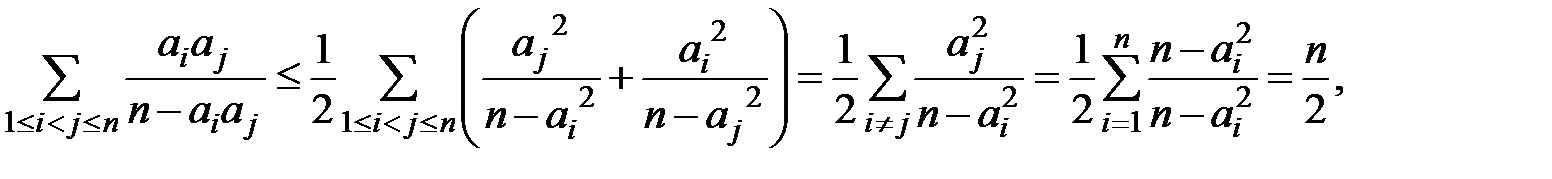
Звідки й випливає нерівність (1).
11 клас
1. При яких натуральних 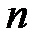 існує такий многочлен
існує такий многочлен 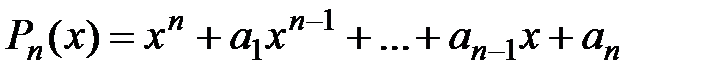 , що для усіх
, що для усіх 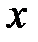
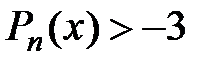 та
та 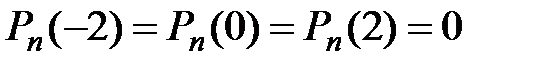 ?
?
Відповідь: 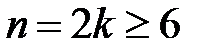 , для
, для 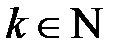 .
.
Розв’язання. З умови, що рівняння має принаймні три корені випливає, що 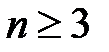 , з нерівності виплаває, що
, з нерівності виплаває, що 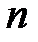 - парне. Для
- парне. Для 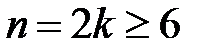 такий многочлен існує, наприклад,
такий многочлен існує, наприклад,
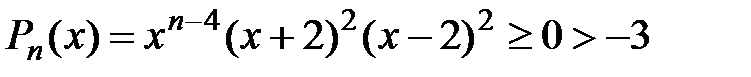 .
.
Покажемо, що для 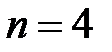 такого многочлена не існує. Методом від супротивного, якщо то не так, і він існує, то він має вигляд
такого многочлена не існує. Методом від супротивного, якщо то не так, і він існує, то він має вигляд 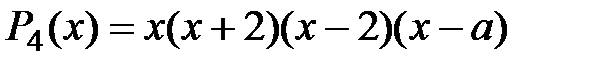 . Але тоді при
. Але тоді при 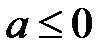
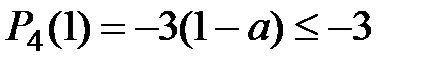 , а при
, а при 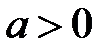
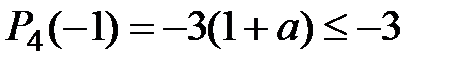 . Одержана суперечність завершує доведення.
. Одержана суперечність завершує доведення.
2. Задача № 3 () за 10 клас.
3. Нехай n – додатнє ціле число таке, що існує додатнє ціле число менше, ніж 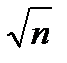 , і не є дільником n. Нехай
, і не є дільником n. Нехай 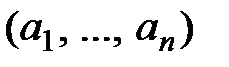 - довільна перестановка чисел
- довільна перестановка чисел 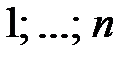 . Нехай
. Нехай 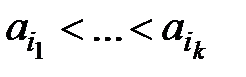 - максимальна зростаюча підпослідовність і нехай
- максимальна зростаюча підпослідовність і нехай 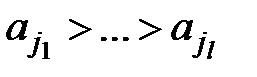 - максимальна спадна підпослідовність. Доведіть, що кортежі
- максимальна спадна підпослідовність. Доведіть, що кортежі 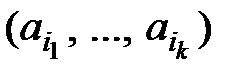 та
та 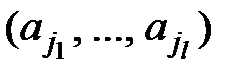 разом (тобто він є хоча б в одному з двох кортежів) містять принаймні одне число, що не є ділльником n.
разом (тобто він є хоча б в одному з двох кортежів) містять принаймні одне число, що не є ділльником n.
Розв’язання. Перший етап доведення складається з того, щоб показати, що 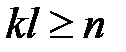 . Для кожного
. Для кожного 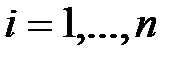 , нехай
, нехай 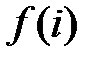 позначає довжину найдовшої зростаючої підпослідовності, що закінчується
позначає довжину найдовшої зростаючої підпослідовності, що закінчується 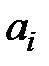 , і нехай
, і нехай 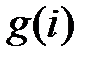 позначає довжину найдовшої спадної підпослідовності, що закінчується
позначає довжину найдовшої спадної підпослідовності, що закінчується 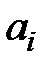 . Для відмінних індексів
. Для відмінних індексів 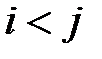 , якщо
, якщо 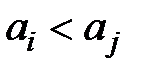 , тоді
, тоді 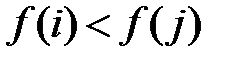 , та якщо
, та якщо 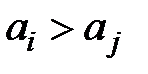 , то
, то 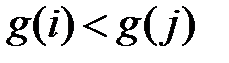 . Отже, пари вигляду
. Отже, пари вигляду 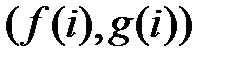 , де
, де 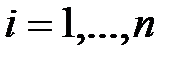 , усі відмінні, тобто загалом є n таких відмінних пар. За умовою задачі, найбільше число серед
, усі відмінні, тобто загалом є n таких відмінних пар. За умовою задачі, найбільше число серед 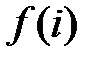 це k, та найбільше число серед
це k, та найбільше число серед 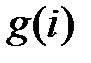 це l. Отже, кількість пар вигляду
це l. Отже, кількість пар вигляду 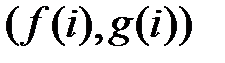 щонайбільше kl. Отже,
щонайбільше kl. Отже, 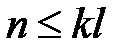 .
.
З цього результату, ми виводимо 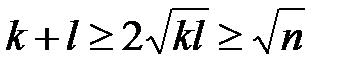 за допомогою теореми про середнє арифметичне та середнє геометричне. Щонайбільше одне число може належати до зростаючої та спадної підпослідовності одночасно. Отже, підпослідовності
за допомогою теореми про середнє арифметичне та середнє геометричне. Щонайбільше одне число може належати до зростаючої та спадної підпослідовності одночасно. Отже, підпослідовності 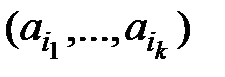 та
та 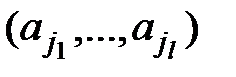 разом містять щонайменше
разом містять щонайменше 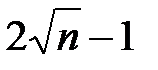 відмінних натуральних чисел загалом. За умовою, число n має щонайбільше
відмінних натуральних чисел загалом. За умовою, число n має щонайбільше 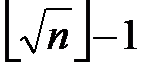 дільників, що не більше, ніж
дільників, що не більше, ніж 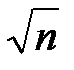 , загальна кількість
, загальна кількість 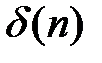 дільників числа n задовольняє нерівності
дільників числа n задовольняє нерівності 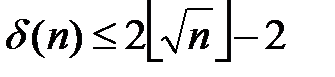 . Отже, підпослідовності
. Отже, підпослідовності 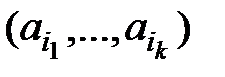 та
та 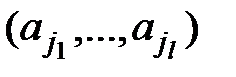 разом містять щонайменше одне число, що не є дільником n.
разом містять щонайменше одне число, що не є дільником n.
4. Задача № 4 () за 10 клас.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|