
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Олімпіада з геометрії
«Ты правда глупый или это имидж? »
Розв’язання задач
9 клас
1. В трикутнику 
 та
та  – середини сторін
– середини сторін 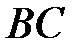 та
та 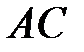 відповідно. Точка
відповідно. Точка 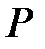 – деяка точка всередині трикутника. Виявилось, що
– деяка точка всередині трикутника. Виявилось, що 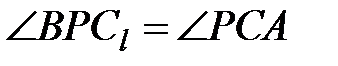 . Доведіть, що
. Доведіть, що 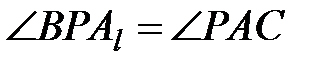 .
.
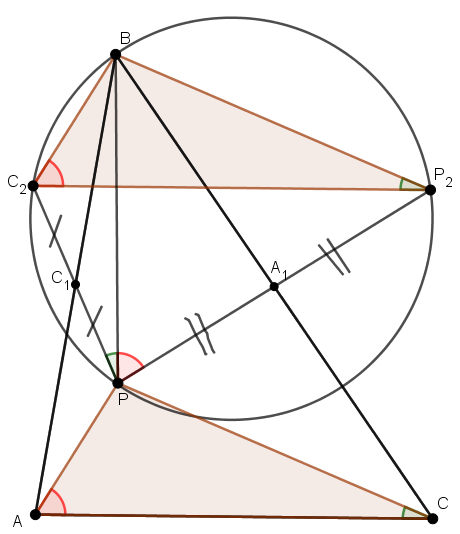
Розв’язання. Нехай точки А2 і С2 симетричні точці Р відносно точок А1 і С1 (рис. 1) відповідно. Тоді, чотирикутники ВРАС2 та ВРСА - паралелограми, звідки трикутник ВС2А2 отримується з трикутника РАС переносом на вектор 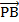 , тому він йому рівний. Звідси,
, тому він йому рівний. Звідси,  ВРС1 =
ВРС1 = 
 ВРС2 =
ВРС2 =  ВА2С2
ВА2С2  ВС2РА2 вписаний
ВС2РА2 вписаний  ВС2А2 =
ВС2А2 =  ВРА2
ВРА2 
 РСА =
РСА =  ВРА1
ВРА1
| Рис. 1 |
 2. Точка
2. Точка  – середина основи
– середина основи 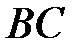 трапеції
трапеції 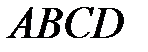 . На основі
. На основі 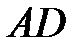 вибрана точка
вибрана точка 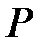 . Пряма
. Пряма 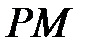 перетинає пряму
перетинає пряму 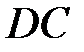 в точці
в точці 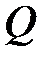 , а перпендикуляр з
, а перпендикуляр з 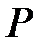 до основ перетинає пряму
до основ перетинає пряму 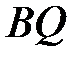 у точці
у точці 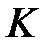 . Доведіть, що
. Доведіть, що 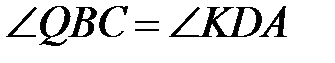 .
.
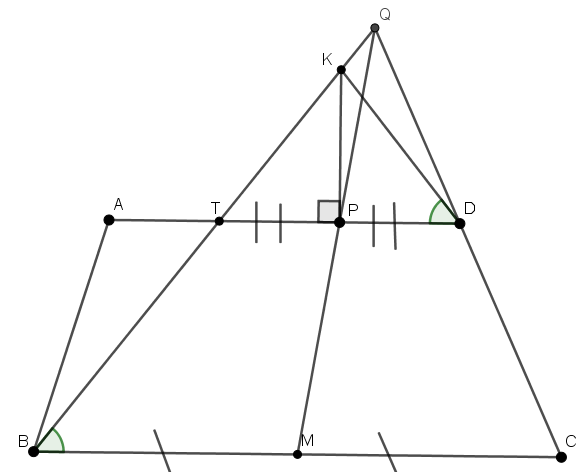
Розв’язання. Нехай прямі BQ та AD перетинаються в точці Т (рис. 2). Використаємо відомий факт: в довільній трапеції точка перетину діагоналей, точка перетину продовжень бічних сторін та середини основ лежать на одній прямій. Застосувавши це до трапеції ВТDC, отримуємо, що P - середина TD. Тоді в трикутнику TDK KP – і висота і медіана, тому він рівнобедрений. Тому  KDA =
KDA =  KDT =
KDT =  KTD =
KTD =  KBC =
KBC =  QBC.
QBC.
| Рис. 2 |
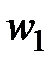 i
i 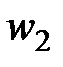 перетинаються в точках
перетинаються в точках 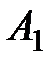 і
і 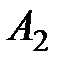 . Нехай
. Нехай  – довільна точка на колі
– довільна точка на колі 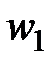 , а пряма
, а пряма 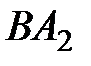 вдруге перетинає коло
вдруге перетинає коло 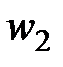 в точці
в точці  . Нехай
. Нехай 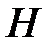 – ортоцентр
– ортоцентр 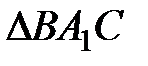 . Доведіть, що для довільного вибору точки
. Доведіть, що для довільного вибору точки  , точка
, точка 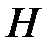 лежить на деякому фіксованому колі.
лежить на деякому фіксованому колі.
Розв’язання. Нехай прямі ВН та СН вдруге перетинають кола w1 i w2 в точках В1, С1 відповідно (рис. 3). Помітимо, що дуга В1А2 = 2  В1ВА2 = 2
В1ВА2 = 2  В1ВС = 180 - 2
В1ВС = 180 - 2  А1СА2 – не залежить від вибору точки В. Це означає, що точки В1 і С1 не змінюються, колі змінюються В і С. Тоді:
А1СА2 – не залежить від вибору точки В. Це означає, що точки В1 і С1 не змінюються, колі змінюються В і С. Тоді:  (B1H, HC1) =
(B1H, HC1) =  (BH, CH) =
(BH, CH) =  (A1C, A1B) =
(A1C, A1B) =  (A1C, CB) +
(A1C, CB) +  (CB, A1B) =
(CB, A1B) =  (A1C, CA2) +
(A1C, CA2) +  (A2B, BA1) – фіксований, що означає, що точка Н знаходиться на деякому колі, що проходить через В1, С1.
(A2B, BA1) – фіксований, що означає, що точка Н знаходиться на деякому колі, що проходить через В1, С1.
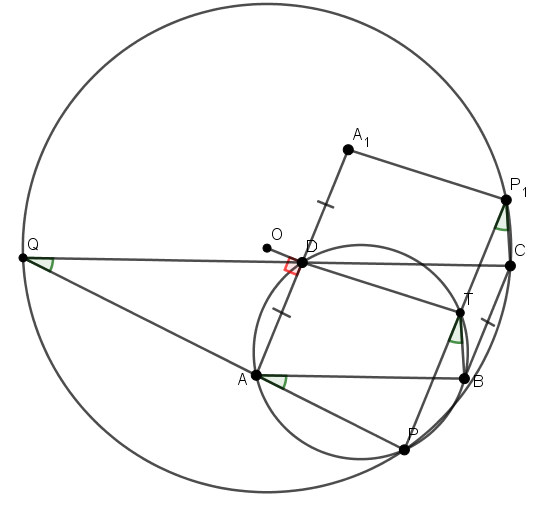 4. В паралелограмі
4. В паралелограмі 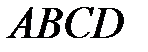
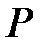 – довільна точка описаного кола
– довільна точка описаного кола 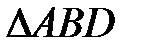 , відмінна від вершин. Пряма
, відмінна від вершин. Пряма 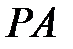 перетинає пряму
перетинає пряму 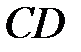 CD в точці
CD в точці 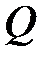 . Нехай
. Нехай  – центр описаного кола
– центр описаного кола 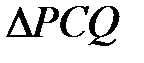 . Доведіть, що
. Доведіть, що 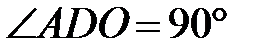 .
.
| Рис. 3 |
Тоді: оскільки чотирикутник АРР1А1 має вісь симетрії – перпендикуляр до сторони AD в точці D, то він – рівнобічна трапеція. А оскільки тоді АDТР – вписана трапеція, то вона також рівнобічна. Тому,  (DT, TP) =
(DT, TP) =  (TP, PA) =
(TP, PA) =  (A1P1, P1P)
(A1P1, P1P)  А1Р1
А1Р1  DT. Звідси, А1Р1ТD – паралелограм. Але чотирикутник DA1CB також паралелограм, адже сторони DA1 та BC рівні та паралельні. Звідси, відрізки Р1Т та СВ також рівні та паралельні, тому чотирикутник Р1ТВС – також паралелограм.
DT. Звідси, А1Р1ТD – паралелограм. Але чотирикутник DA1CB також паралелограм, адже сторони DA1 та BC рівні та паралельні. Звідси, відрізки Р1Т та СВ також рівні та паралельні, тому чотирикутник Р1ТВС – також паралелограм.
Звідси,  (PQ, QC) =
(PQ, QC) =  (PA, AB) =
(PA, AB) =  (PT, TB) =
(PT, TB) =  (PP1, P1C), звідки чотирикутник PQP1C вписаний, з центром О. Тоді О лежить на серединному перпендикулярі до відрізка РР1, що співпадає з перпендикуляром до AD в точці D. Тому,
(PP1, P1C), звідки чотирикутник PQP1C вписаний, з центром О. Тоді О лежить на серединному перпендикулярі до відрізка РР1, що співпадає з перпендикуляром до AD в точці D. Тому,  АDO = 90.
АDO = 90.
10 клас
1. Задача № 1 () за 9 клас.
| Рис. 4 |
2. Задача № 3 () за 9 клас.
3. На гіпотенузі 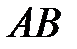 прямокутного трикутника
прямокутного трикутника 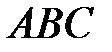 позначили таку точку
позначили таку точку 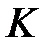 , що
, що 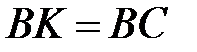 . Нехай
. Нехай 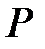 – точка на перпендикулярі з точки
– точка на перпендикулярі з точки 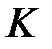 до прямої
до прямої 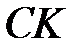 , рівновіддалена від точок
, рівновіддалена від точок 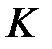 і
і 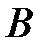 . Нехай також
. Нехай також 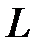 – середина відрізка
– середина відрізка 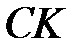 . Доведіть, що пряма
. Доведіть, що пряма 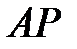 дотикається описаного кола
дотикається описаного кола 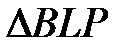 .
.
Розв’язання. Нехай ВТ – бісектриса трикутника, а точка Р1 симетрична точці Т відносно точки К (рис. 5). Трикутники СТВ та ТВК рівні за двома сторонами та кутом між ними, отже,  ТКВ =
ТКВ =  С = 90. Помітимо, що з цього випливає, що чотирикутник СТКВ вписаний з діаметром ТВ. Тоді, оскільки в трикутнику ТВР1 ВК – медіана і висота, то він рівнобедрений, а трикутники КВР1, ТВК, СВТ рівні. Оскільки
С = 90. Помітимо, що з цього випливає, що чотирикутник СТКВ вписаний з діаметром ТВ. Тоді, оскільки в трикутнику ТВР1 ВК – медіана і висота, то він рівнобедрений, а трикутники КВР1, ТВК, СВТ рівні. Оскільки  КР1В =
КР1В =  СТВ =
СТВ =  СКВ, то пряма СК дотикається описаного кола трикутника КР1В. Нехай О – центр цього кола. Тоді маємо: ОК
СКВ, то пряма СК дотикається описаного кола трикутника КР1В. Нехай О – центр цього кола. Тоді маємо: ОК  СК і ОВ = ОК, тому О співпадає з Р. Отож, Р – центр описаного кола ВКР1, а тому співпадає з серединою ВР1.
СК і ОВ = ОК, тому О співпадає з Р. Отож, Р – центр описаного кола ВКР1, а тому співпадає з серединою ВР1.
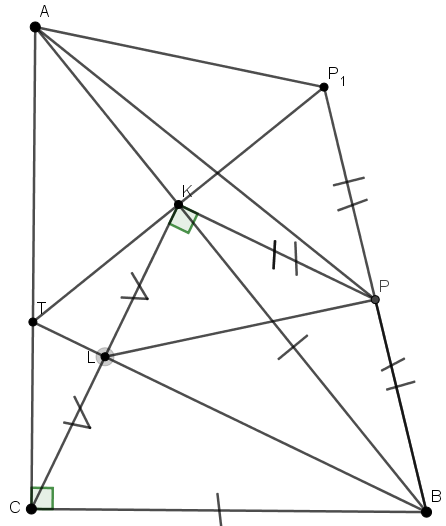 Помітимо тепер, що трикутники АР1В і АКС – подібні за всіма кутами:
Помітимо тепер, що трикутники АР1В і АКС – подібні за всіма кутами:  Р1АК =
Р1АК =  ВАС з симетрії, а
ВАС з симетрії, а  Р1ВА =
Р1ВА =  КВТ =
КВТ =  КСА. Оскільки Р і L – середини відповідних сторін, то трикутники АРВ і АLC також подібні. Звідси, існує поворотна гомотетія з центром в точці А, що переводить C в В, а L в Р. Це означає, що трикутники ALP та АСВ також подібні. Тоді
КСА. Оскільки Р і L – середини відповідних сторін, то трикутники АРВ і АLC також подібні. Звідси, існує поворотна гомотетія з центром в точці А, що переводить C в В, а L в Р. Це означає, що трикутники ALP та АСВ також подібні. Тоді  АРL =
АРL =  АВС = 2
АВС = 2  АВL =
АВL =  РВL. Отже, пряма AP дотикається до описаного кола трикутника PBL.
РВL. Отже, пряма AP дотикається до описаного кола трикутника PBL.
| Рис. 5 |
 з гіпотенузою
з гіпотенузою  вписане коло дотикається до катетів
вписане коло дотикається до катетів 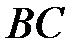 і
і 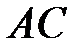 у точках
у точках 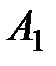 і
і 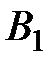 відповідно. Пряма, що містить середню лінію
відповідно. Пряма, що містить середню лінію 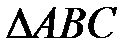 , що паралельна
, що паралельна 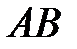 , перетинає його описане коло в точках
, перетинає його описане коло в точках 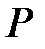 та
та 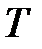 . Доведіть, що точки
. Доведіть, що точки 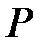 ,
, 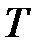
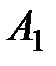 і
і 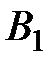 лежать на одному колі.
лежать на одному колі.
Розв’язання. Нехай СН – висота трикутника, І – центр вписаного кола, а О – точка перетину прямих РТ і А1С1. Оскільки  С = 90, то трикутники СВ1І та СА1І – прямокутні рівнобедрені, тому пряма В1А1 – серединний перпендикуляр до СІ. Оскільки РТ – середня лінія трикутника АВС – є серединним перпендикуляром до СН, то О – центр описаного кола трикутника СІН (рис. 6).
С = 90, то трикутники СВ1І та СА1І – прямокутні рівнобедрені, тому пряма В1А1 – серединний перпендикуляр до СІ. Оскільки РТ – середня лінія трикутника АВС – є серединним перпендикуляром до СН, то О – центр описаного кола трикутника СІН (рис. 6).
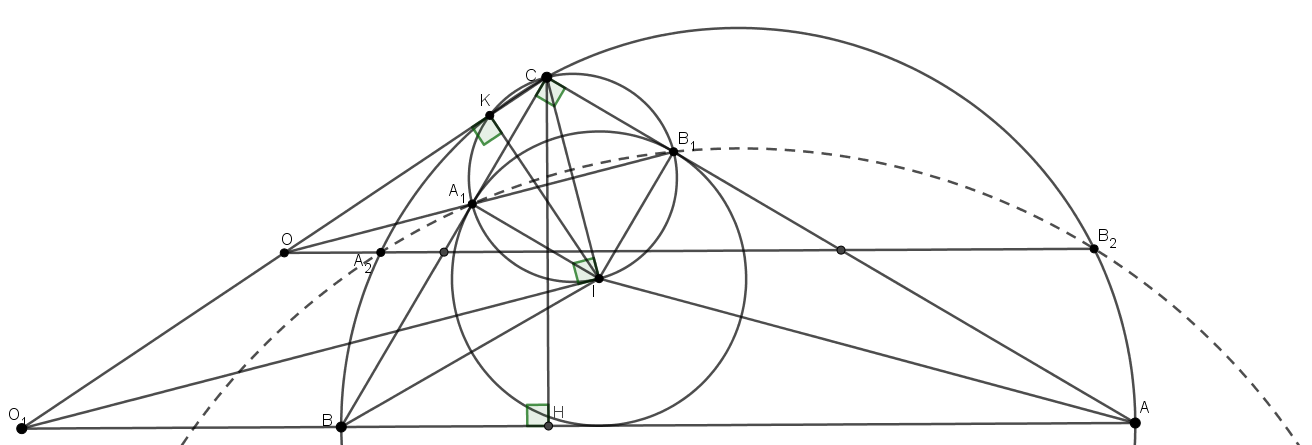
Нехай точка О1 симетрична точці С відносно О. Тоді, очевидно, що оскільки О лежить на середній лінії трикутника, то О1 лежить на прямій АВ. Також, СО1 – діаметр кола СІНО1, тому  СІО1 = 90. Оскільки центр описаного кола АІВ (середина дуги АВ, що не містить точки С) лежить на прямій СІ, перпендикулярній О1І, то О1І – дотична до описаного кола трикутника АІВ.
СІО1 = 90. Оскільки центр описаного кола АІВ (середина дуги АВ, що не містить точки С) лежить на прямій СІ, перпендикулярній О1І, то О1І – дотична до описаного кола трикутника АІВ.
Нехай пряма ОС перетинає описане коло трикутника АВС другий раз в точці К. Використовуючи степінь точки, маємо: О1К  О1С = О1А
О1С = О1А  О1В = О1І2, звідки ІК – висота в прямокутному О1ІС, і
О1В = О1І2, звідки ІК – висота в прямокутному О1ІС, і  СКІ = 90. З цього випливає, що точки С, К, А1, В1, І лежать на одному колі з діаметром СІ. Тому, ОВ1
СКІ = 90. З цього випливає, що точки С, К, А1, В1, І лежать на одному колі з діаметром СІ. Тому, ОВ1  ОА1 = ОС
ОА1 = ОС  ОК = ОР
ОК = ОР  ОТ, звідки точки Р, Т, В1, А1 лежать на одному колі.
ОТ, звідки точки Р, Т, В1, А1 лежать на одному колі.
| Рис. 6 |
11 клас
1. Задача № 1 () за 9 клас.
2. На стороні 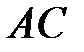 трикутника
трикутника 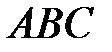 знайшлась така точка
знайшлась така точка 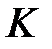 , що
, що 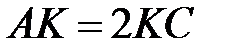 і
і 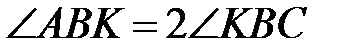 . Нехай
. Нехай 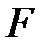 – середина
– середина 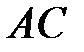 ,
, 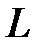 – проекція
– проекція 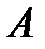 на
на 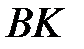 . Доведіть, що
. Доведіть, що 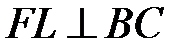 .
.
Розв’язання. Нехай Т – точка, що симетрична А відносно L (рис. 7)
 Помітимо, що четвірка точок (С, К, F, A) – гармонічна (CK/KF = CA/AF = 2). Тоді коло з діаметром АК, на якому лежить L – коло Аполлонія, звідки CL = 2FL = CT (адже FL – середня лінія трикутника АСТ). Помітимо також, що
Помітимо, що четвірка точок (С, К, F, A) – гармонічна (CK/KF = CA/AF = 2). Тоді коло з діаметром АК, на якому лежить L – коло Аполлонія, звідки CL = 2FL = CT (адже FL – середня лінія трикутника АСТ). Помітимо також, що  ТВС =
ТВС =  ТВК -
ТВК -  СВК =
СВК =  АВК -
АВК -  СВК =
СВК =  СВК. Отож, С – точка перетину бісектриси кута TBL та серединного перпендикуляру до сторони TL трикутника TCL. Оскільки ТВ> BL, як гіпотенуза, то трикутник нерівнобедрений, і ці прямі не співпадають. В такому разі, С – середина дуги TL описаного кола трикутника TBL, що не містить точку В. Тоді,
СВК. Отож, С – точка перетину бісектриси кута TBL та серединного перпендикуляру до сторони TL трикутника TCL. Оскільки ТВ> BL, як гіпотенуза, то трикутник нерівнобедрений, і ці прямі не співпадають. В такому разі, С – середина дуги TL описаного кола трикутника TBL, що не містить точку В. Тоді,  ТСВ =
ТСВ =  TLB = 90. Отже, TC
TLB = 90. Отже, TC  BC. Оскільки FL
BC. Оскільки FL  TC, то і FL
TC, то і FL  BC.
BC.
| Рис. 7 |
3. Задача № 4 () за 9 клас.
4. Нехай 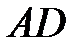 – внутрішня бісектриса трикутника
– внутрішня бісектриса трикутника 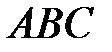 . Перпендикуляр до сторони
. Перпендикуляр до сторони 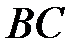 у точці
у точці 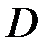 перетинає зовнішню бісектрису
перетинає зовнішню бісектрису 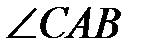 в точці
в точці 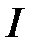 . Коло з центром
. Коло з центром 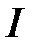 і радіусом
і радіусом  перетинає сторони
перетинає сторони 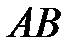 і
і 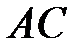 в точках
в точках 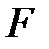 i
i 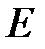 відповідно.
відповідно. 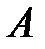 -симедіана
-симедіана 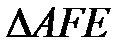 перетинає описане коло
перетинає описане коло 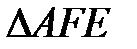 вдруге в точці
вдруге в точці 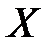 . Доведіть, що описані кола
. Доведіть, що описані кола 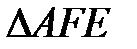 та
та 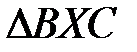 дотикаються.
дотикаються.
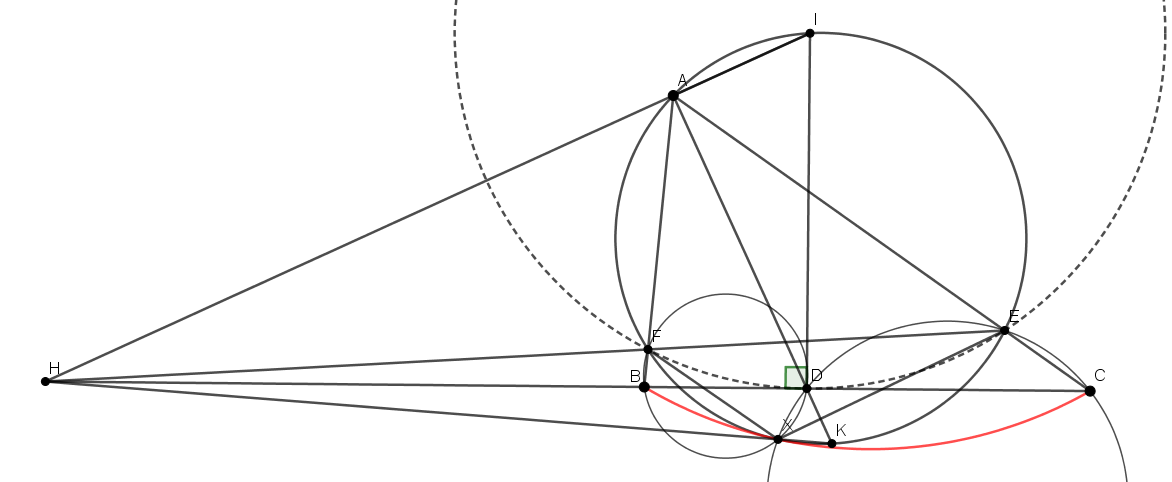
Розв’язання. Нехай К – середина дуги FE описаного кола трикутника AFE, що не містить точку А. Тоді КІ – діаметр цього кола. Нехай промінь КХ перетинає пряму FE в точці Н. Тоді, оскільки КX – зовнішня бісектриса кута FXE, то HF/HE = FX/FE = AF/FE. Звідси маємо, що Н – основа зовнішньої бісектриси кута А трикутника AFE. Тому, Н лежить на прямій АІ (рис. 8).
Розглянемо тепер радикальні осі трьох кіл: FAIE, FDE, ADI. Помітимо, що обидва кола FDE та AID дотикаються до сторони ВС в точці D. Отже, радикальними осями будуть прямі: ВС, FE, AI, тому вони мають перетинатись в одній точці. Отже, точка КН лежить і на прямій ВС.
Оскільки КІ – діаметр описаного кола трикутника AFE, то  ІХК = 90, тому
ІХК = 90, тому  НХІ = 90. З цього випливає, що точки Н, Х, І, D лежать на одному колі з діаметром HI.
НХІ = 90. З цього випливає, що точки Н, Х, І, D лежать на одному колі з діаметром HI.
Тепер:  (BD, DX) =
(BD, DX) =  (KD, DX) =
(KD, DX) =  (KI, IX) =
(KI, IX) =  (AI, IX) =
(AI, IX) =  (AF, FX) =
(AF, FX) =  (BF, FX). Отже, чотирикутник BFDX вписаний. Аналогічно, XDEC вписаний. Тоді залишилось порахувати кути:
(BF, FX). Отже, чотирикутник BFDX вписаний. Аналогічно, XDEC вписаний. Тоді залишилось порахувати кути:
Нехай l – дотична до описаного кола трикутника AFE в точці Х. Тоді:  (l, XC) =
(l, XC) =  (l, XE) +
(l, XE) +  (XE, XC) =
(XE, XC) =  (FX, FE) +
(FX, FE) +  (DE, DC) =
(DE, DC) =  (FX, FE) +
(FX, FE) +  (FE, FD) =
(FE, FD) =  (FX, FD) =
(FX, FD) =  (BX, BD). Звідси випливає, що пряма l є спільною дотичною до кіл FXE i BXC в точці Х, а тому вони дотикаються.
(BX, BD). Звідси випливає, що пряма l є спільною дотичною до кіл FXE i BXC в точці Х, а тому вони дотикаються.
| Рис. 8 |
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|