
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Екі белгісізі бар, тригонометриялық теңдеуді шешу.
Екі белгісізі бар, тригонометриялық тең деуді шешу.
Тригонометриялық тең деулерді шешу барысында бірінші тең деудің екі белгісізі х жә не у айнымалысы бар, тригонометриялық тең деу болып келу мү мкін, ал екіншісі сызық ты тең деу ретінде берілу мү мкін. Бұ ндай тригонометриялық жү йелерді шешу ү шін бір тең деудің белгісізін тауып алып, екінші тең деуге сала отырып шығ арамыз.
МЫСАЛ 1. Жү йені шешің із:
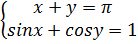
ШЕШІМІ. Бірінші тең деудің y мә нін алайық:
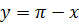 ,
,
y мә нінекінші тең деуге салайық:

Кө ріп тұ рғ анымыздай қ арапайым тригонометриялық тең деуге келтірілді. Тең деудің шешімін екі тү рде жазайық:
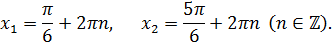
Енді y белгісізміздің мә нін табайық:

Жү йелергесайжауапты(x; y) тү рінде береміз.
ЖАУАБЫ:
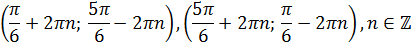
МЫСАЛ 2. Жү йені шешің із:
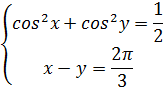
ШЕШІМІ.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|