
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Практическая работа 2. Теоретический материал. Абсолютная и относительная погрешность. ОПР. Модуль разности между точным числом А и его приближенным значением a называется абсолютной погрешностью числа а.. ОПР. Границей абсолютной погрешности (ее предельн
Практическая работа 2
Тема. Приближенные значения. Абсолютная и относительная погрешность.
Цель работы: формирование умений и навыков вычисления приближенных величин и определения точности приближения.
Продолжительность: 90 мин.
Оснащение: инструкционно – технологические карты, тетради для практических работ.
Методические указания по выполнению работы:
· изучите теоретический материал с оформление конспекта;
· изучите условия задания практического занятия;
· при выполнении работы соблюдайте последовательность заданий;
· оформите отчет в тетради для практических работ, сформулируйте выводы о проделанной работе.
Порядок проведения работы:
Используя теоретические сведения и примеры, выполнить практическую часть.
Теоретический материал
Абсолютная и относительная погрешность
ОПР. Модуль разности между точным числом А и его приближенным значением a называется абсолютной погрешностью числа а.
ОБОЗНАЧЕНИЕ:  абсолютная погрешность числа а
абсолютная погрешность числа а
 , где А – точное значение числа, а – его приближенное значение.
, где А – точное значение числа, а – его приближенное значение.
ПРИМЕР. Найдите абсолютную погрешность округления до единиц следующих чисел:
А) 0, 8 ≈ 1 А = 0, 8 – точное значение, а = 1 – приближенное значение
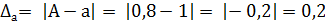
Б) 563, 58 ≈ 564 А = 563, 58 а = 564
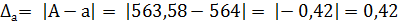
ОПР. Границей абсолютной погрешности (ее предельным значением) называется возможно меньшее число Δ, про которое известно, что.
На практике мы вынуждены брать значение числа Δ с запасом, т. к. точное значение А, как правило, остается неизвестным и, следовательно, невозможно вычислить  . Значение а и Δ позволяет установить границы, в которых лежит точное число А, поскольку из неравенства
. Значение а и Δ позволяет установить границы, в которых лежит точное число А, поскольку из неравенства 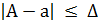 следует
следует
- Δ 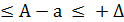 ;
;
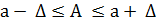 .
.
ПРИМЕР. А = 2, 21 ± 0, 01 означает, что 2, 21 – 0, 01 ≤ А ≤ 2, 21 + 0, 01
2, 2 ≤ А ≤ 2, 22
ВАЖНО! Если а – приближенное значение числа А, причем абсолютная погрешность равна Δ, то говорят, что а есть приближенное значение числа А с точностью до Δ.
а = 2, 21 – приближенное значение числа А
Δ = 0, 01 – абсолютная погрешность
«2, 21 – приближенное значение числа А с точностью до 0, 01»
Пример1. Пусть дано 3, 8 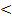 х
х 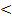 4, 2. Найти границы выражения: А) 3х; Б) -2х+5
4, 2. Найти границы выражения: А) 3х; Б) -2х+5
Решение:
А) умножим все члены данного неравенства на 3,
3*3, 8 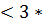 х
х 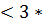 4, 2
4, 2
Получаем
11, 4 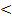 3х
3х 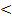 12, 6
12, 6
Б) умножим все члены данного неравенства на -2,
-2*3, 8  х
х  4, 2
4, 2
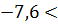 -2х
-2х 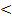 -8, 4
-8, 4
При умножении на отрицательное число знак меняется в другую сторону
Получаем
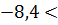 -2х
-2х 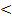 -7, 6
-7, 6
Теперь прибавим ко всем членам данного неравенства 5
5 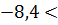 5-2х
5-2х 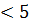 -7, 6
-7, 6
Получаем
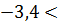 -2х+5
-2х+5 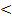 -2, 6
-2, 6
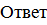 : а) 11, 4
: а) 11, 4 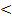 3х
3х 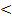 12, 6; б)
12, 6; б) 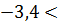 -2х+5
-2х+5 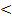 -2, 6
-2, 6
Пример 2. Пусть дано 6, 2 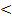 х
х 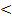 8, 4. Найти границы величины
8, 4. Найти границы величины  .
.
Решение: х  0
0
Так как х 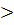 6, 2 то
6, 2 то 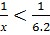 или
или 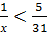
Но х  8, 4, то
8, 4, то 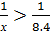 или
или 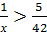
Получаем
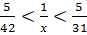 ;
; 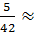 0, 119…
0, 119… 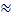 0, 11;
0, 11;  0, 156…
0, 156… 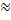 0, 16
0, 16
Получаем 0, 11 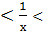 0, 16
0, 16
Ответ: 0, 11 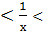 0, 16
0, 16
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|