
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Признак перпендикулярности прямой и плоскости
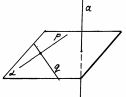 рис. 4 рис. 4
| Теорема: Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в одной плоскости, то она перпендикулярна к этой плоскости. |
Замечания:
1. Через любую точку пространства проходит плоскость, перпендикулярная к данной прямой, и притом единственная.
2. Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.
3. Если две плоскости перпендикулярны к прямой, то они параллельны.
Определение: Наклонной, проведённой из данной точки к данной плоскости, называется любой отрезок, соединяющий данную точку с точкой плоскости, не являющийся перпендикуляром к плоскости.
- Конец отрезка, лежащий в плоскости, называется основанием наклонной.
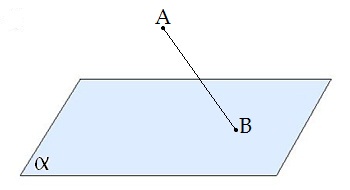
AB — наклонная;
B — основание наклонной.
Определение: Перпендикуляром, проведённым из данной точки к данной плоскости, называется отрезок, соединяющий данную точку с точкой плоскости, и лежащий на прямой, перпендикулярной плоскости.
- Конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра.
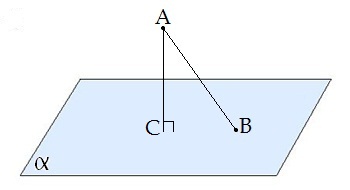
AC — перпендикуляр;
C — основание перпендикуляра.
- Расстоянием от точки до плоскости называется длина перпендикуляра, проведённого из этой точки к плоскости.
- Отрезок, соединяющий основания перпендикуляра и наклонной, проведённых из одной и той же точки, называется проекцией наклонной.
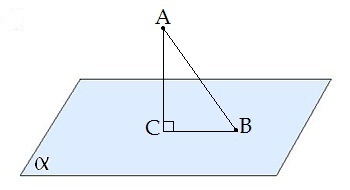
CB — проекция наклонной AB на плоскость α.
- Треугольник ABC прямоугольный.
- Углом между наклонной и плоскостью называется угол между этой наклонной и её проекцией на плоскость.
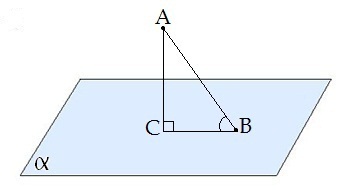
∢ CBA — угол между наклонной AB и плоскостью α.
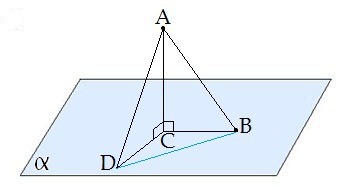
Если AD> AB, то DC> BC.
- Если из данной точки к данной плоскости провести несколько наклонных, то большей наклонной соответствует большая проекция.
∢ DAB — угол между наклонными; а ∢ DCB — угол между проекциями.
Отрезок DB — расстояние между основаниями наклонных.
Теорема о трёх перпендикулярах: Если прямая, проведённая на плоскости через основание наклонной, перпендикулярна её проекции, то она перпендикулярна и самой наклонной.
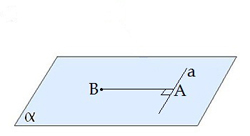 a⊥ AB
a⊥ AB
| 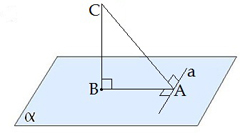 a⊥ AB, BC⊥ BA}⇒ a⊥ CA
a⊥ AB, BC⊥ BA}⇒ a⊥ CA
|
Справедлива также обратная теорема:
Если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.
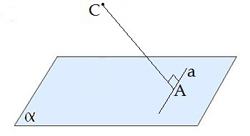 a⊥ AC
a⊥ AC
|
 a⊥ AC, BC⊥ BA}⇒ a⊥ BA
a⊥ AC, BC⊥ BA}⇒ a⊥ BA
|
Пример: Из вершины S к плоскости квадрата ABCD проведён перпендикуляр BS и наклонные SA, SC и SD. Назови все прямоугольные треугольники с вершиной S, обоснуй свой ответ.
Рисунок:
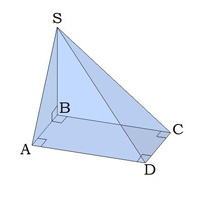 ABCD — квадрат, все углы которого равны по 90° градусов.
1. Грань ASB — прямоугольный треугольник,
2. Грань BSC — прямоугольный треугольник, т. к. BS — перпендикуляр к плоскости.
ABCD — квадрат, все углы которого равны по 90° градусов.
1. Грань ASB — прямоугольный треугольник,
2. Грань BSC — прямоугольный треугольник, т. к. BS — перпендикуляр к плоскости.
|
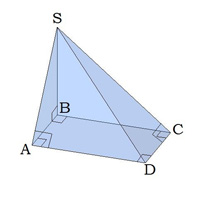 3. Грань DSC — прямоугольный треугольник, по теореме о трёх перпендикулярах:
CD⊥ BC, т. к. ABCD− квадратSB⊥ BC, т. к. перпендикуляр}⇒ CD⊥ SC; значит, ∢ SCD= 90°.
4. Грань ASD — прямоугольный треугольник, по теореме о трёх перпендикулярах:
AD⊥ AB, т. к. ABCD− квадратSB⊥ AB, т. к. перпендикуляр}⇒ AD⊥ SA;
значит, ∢ SAD= 90°.
3. Грань DSC — прямоугольный треугольник, по теореме о трёх перпендикулярах:
CD⊥ BC, т. к. ABCD− квадратSB⊥ BC, т. к. перпендикуляр}⇒ CD⊥ SC; значит, ∢ SCD= 90°.
4. Грань ASD — прямоугольный треугольник, по теореме о трёх перпендикулярах:
AD⊥ AB, т. к. ABCD− квадратSB⊥ AB, т. к. перпендикуляр}⇒ AD⊥ SA;
значит, ∢ SAD= 90°.
|
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|