
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
11 декабря 2021 года. Тема Связь между знаком производной функции и возрастанием и убыванием.
11 декабря 2021 года
Тема Связь между знаком производной функции и возрастанием и убыванием.
Разобраться в решении приведенных примеров и подробно записать их решения и схемы в тетради для индивидуального обучения.
ВАЖНО!
- Если производная функции в каждой точке некоторого промежутка положительная, то функция на этом промежутке возрастает.
- Если производная в каждой точке промежутка отрицательная, то функция на этом промежутке убывает.
- Если производная в каждой точке промежутка тождественно равна нулю, то на этом промежутке функция постоянная.
Следовательно, чтобы определить промежутки возрастания и убывания функции 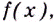 нужно решить неравенства
нужно решить неравенства 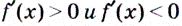 или найти все критические точки функции, разбить ими область определения функции на промежутки, а потом исследовать, на каких из них функция возрастает, а на каких — убывает.
или найти все критические точки функции, разбить ими область определения функции на промежутки, а потом исследовать, на каких из них функция возрастает, а на каких — убывает.
Пример 1:
Найдите промежутки возрастания и убывания функции 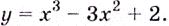
Решение:
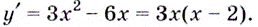 необходимо определить критические точки (в этих точках производная равна 0). Т. е производную надо приравнять 0.
необходимо определить критические точки (в этих точках производная равна 0). Т. е производную надо приравнять 0.
Уравнение 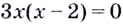 имеет корни
имеет корни 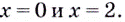 Это — критические точки. Область определения данной функции — множество
Это — критические точки. Область определения данной функции — множество 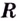 — они разбивают на три промежутка:
— они разбивают на три промежутка: 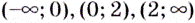 (рис. 1). Производная функции на этих промежутках имеет соответственно такие знаки:
(рис. 1). Производная функции на этих промежутках имеет соответственно такие знаки: 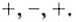 Следовательно, данная функция на промежутках
Следовательно, данная функция на промежутках 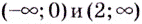 возрастает, а на
возрастает, а на 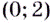 убывает.
убывает.
Замечание: Если функция непрерывна в каком-нибудь конце промежутка возрастания или убывания, то эту точку можно присоединить к рассматриваемому промежутку. Поскольку функция 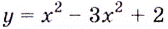 в точках 0 и 2 непрерывна, то можно утверждать, что она возрастает на промежутках
в точках 0 и 2 непрерывна, то можно утверждать, что она возрастает на промежутках 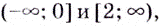 на
на 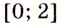 — убывает.
— убывает.
Пример 2:
Найдите промежутки убывания функции 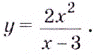
Решение:
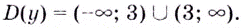
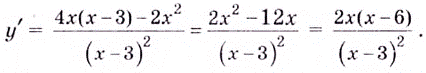
Критические точки: 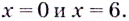 Они всю область определения функции разбивают на интервалы:
Они всю область определения функции разбивают на интервалы: 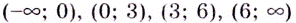 (рис. 2). Производная
(рис. 2). Производная 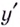 на этих промежутках имеет соответственно такие знаки:
на этих промежутках имеет соответственно такие знаки: 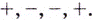 Следовательно, функция убывает на промежутках
Следовательно, функция убывает на промежутках 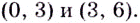 Поскольку в точках
Поскольку в точках 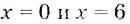 данная функция непрерывна, то ответ можно записать и так:
данная функция непрерывна, то ответ можно записать и так: 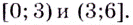
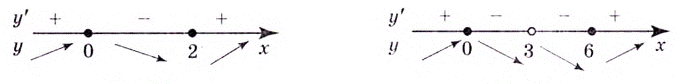
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|