
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
КОМПЛЕКСНЫЕ ЧИСЛА. Понятие комплексного числа. a+bi – это ЕДИНОЕ ЧИСЛО, а не сложение. Действительную и мнимую части комплексного числа, в принципе, можно переставить местами:z= bi + a или переставить мнимую единицу:z= a + ib – от этого комплексное число
КОМПЛЕКСНЫЕ ЧИСЛА
Понятие комплексного числа
Числа вида a+bi, где a; b – действительные числа, число i определяется равенством i2 = - 1, называются КОМПЛЕКСНЫМИ числами.
Примеры: 3+2i; -7+I; 5-8i; -2-4i; ½ + (3/2)i и т. п.
i – мнимая единица. z - комплексное число.
z = a + bi –алгебраическая форма комплексного числа.
а – действительная часть комплексного числа(Re z)
b – мнимая часть комплексного числа(Im z).
0 = 0 + 0i – комплексный ноль
1 = 1 + 0i – действительная единица
i = 0 + i - мнимая единица
Представить комплексное число «в жизни» – это всё равно, что пытаться представить четвертое измерение в нашем трехмерном пространстве. Комплексное число – это двумерное число.
a+bi – это ЕДИНОЕ ЧИСЛО, а не сложение. Действительную и мнимую части комплексного числа, в принципе, можно переставить местами: z= bi + a или переставить мнимую единицу: z= a + ib – от этого комплексное число не изменится. Но стандартно комплексное число принято записывать именно в таком порядке: z= a +bi
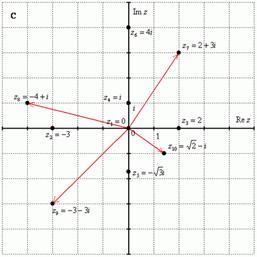
Комплексные числа изображаются на комплексной плоскости:
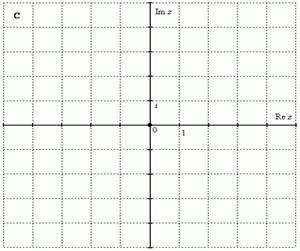
R -множество действительных чисел. Множество же комплексных чисел принято обозначать «жирной» или утолщенной буквой C. Поэтому на чертеже следует поставить букву C, обозначая тот факт, что у нас комплексная плоскость.
Комплексная плоскость состоит из двух осей:
Re z – действительная ось
Im z – мнимая ось
Правила оформления чертежа такие же, как и для чертежа в декартовой системе координат. По осям нужно задать масштаб, отмечаем ноль, единицу 1 по действительной оси, единицу I по мнимой оси.
Построим на комплексной плоскости следующие комплексные числа:
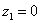 ,
, 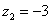 ,
, 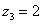
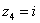 ,
, 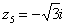 ,
, 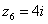
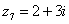 ,
, 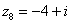 ,
, 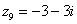 ,
, 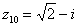
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|