Контакты

Случайная статья

Пример 4.. Для их вычисления необходимо представить дробь в виде суммы более простых дробей. Рассмотрим решение этой задачи на примерах.

⇐ ПредыдущаяСтр 2 из 3Следующая ⇒

Пример 4.

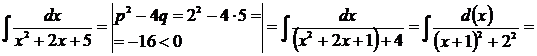
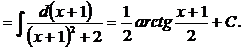
4) Вычисление интегралов вида ,

где 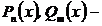многочлены, n< m – степени многочленов.

Для их вычисления необходимо представить дробь в виде суммы более простых дробей. Рассмотрим решение этой задачи на примерах.

Пример 5. Найти интеграл .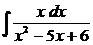

Решение. Так как корнями знаменателя являются х₁= 2 и х₂= 3, то знаменатель раскладывается на множители .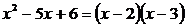

Представим теперь дробь в виде следующей суммы:

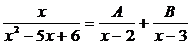и найдем коэффициенты А и В.

Приведем дроби в правой части к общему знаменателю:

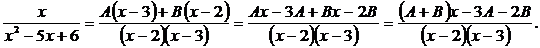
Так как это – тождество, то, приравняв числители, получим

.

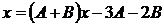Приравнивая коэффициенты при одинаковых степенях х в обеих частях тождества, составим систему уравнений:

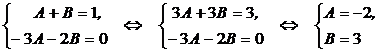
Таким образом, .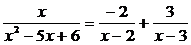

Итак,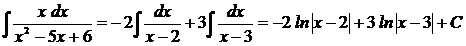

или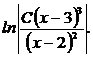

Пример 6. Найти интеграл .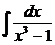

Решение. Так как 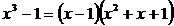, то представим дробь в виде следующей суммы:

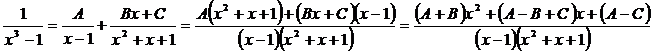Итак, .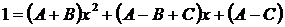

Приравнивая коэффициенты при одинаковых степенях х в обеих частях тождества, составим систему уравнений:

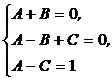
Решив систему, получим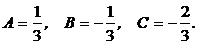

Следовательно,

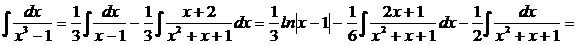
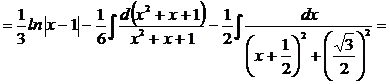
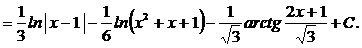
3. Решение упражнений. Найти интегралы:

1) ;

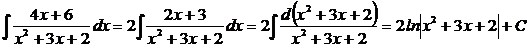2) ;

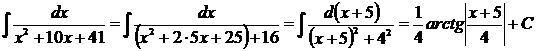3) ;

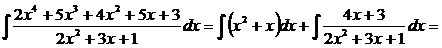
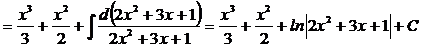4) ;

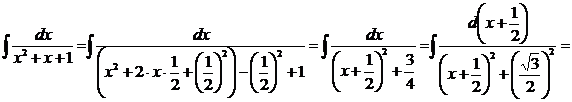
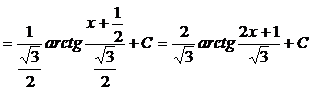5) .

⇐ Предыдущая 123 Следующая ⇒

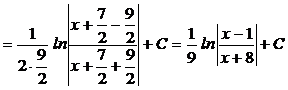© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.