Занятие № 90. Раздел 11. Многогранники и круглые тела . Тема: Пирамида. Правильная пирамида. Усеченная пирамида. Тетраэдр. Симметрия в пирамиде. Сечения пирамиды.. Пирамида и ее свойства.

Занятие № 90

Раздел 11. Многогранники и круглые тела

Тема: Пирамида. Правильная пирамида. Усеченная пирамида. Тетраэдр. Симметрия в пирамиде. Сечения пирамиды.

Задание: Атанасян Л. С. Геометрия. 10-11 кл., гл. 3, § 2, п. 32-34; Погорелов А. В. Геометрия. 10-11 кл., §5, п. 47-50; конспект лекции; ответить на контрольные вопросы.

Пирамида и ее свойства.

Пирамидой (n-угольной) называется многогранник, у которого одна грань является произвольным n-угольником, а остальные п граней – треугольники, имеющие общую вершину. На рис. 1 изображена пирамида SABCD.

n-угольник называется основанием, а треугольники – боковыми гранями. Общая вершина боковых граней называется вершиной пирамиды.

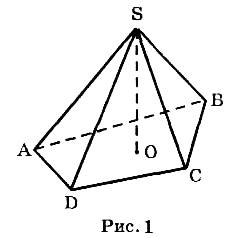
На рис. 1 ABCD - основание;

ASAB, ASBC, ASCD, ASDA – боковые грани пирамиды; S – вершина пирамиды; SA, SB, SC, SD – боковые ребра.

Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на плоскость основания. На рис. 1 SO – высота пирамиды.

Правильной пирамидой называется пирамида, в основании которой лежит правильный многоугольник, а основание высоты пирамиды совпадает с центром этого многоугольника.

Высота боковой грани правильной пирамиды, проведенная из вершины пирамиды, называется ее апофемой.

На рис. 2 изображена правильная треугольная пирамида SABC, SK^CB, SK – апофема.

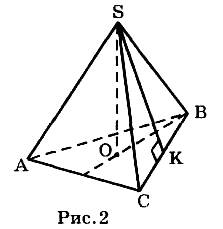
У правильной пирамиды:

— боковые ребра равны;

— боковые грани равны;

— апофемы равны;

— двугранные углы при основании равны;

— двугранные углы при боковых ребрах равны;

— каждая точка высоты правильной пирамиды равноудалена от всех вершин основания;

— каждая точка высоты правильной пирамиды равноудалена от всех боковых граней;

— каждая точка высоты правильной пирамиды равноудалена от всех боковых ребер.

Диагональным сечением пирамиды называется сечение плоскостью, проходящей через два боковых ребра пирамиды, не лежащих в одной грани.

Свойства параллельных сечений пирамиды Теорема. Если пирамида пересечена плоскостью параллельной основанию, то:

1) боковые ребра и высота пирамиды делятся этой плоскостью на пропорциональные части;

2) сечение – многоугольник, подобный основанию;

3) площади сечения и основания относятся как квадраты их расстояний от вершины.

12 Следующая ⇒