Контакты

Случайная статья

Опредление степени с действительным показателем.

⇐ ПредыдущаяСтр 2 из 3Следующая ⇒

Опредление степени с действительным показателем.

При любом действительном х 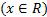и любом положительном а 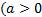) степень 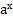является положительным числом:

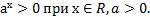
Но если основание степени а=0, то степень 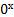определяют только при 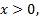и считают, что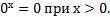

При 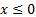выражение 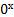не имеет смысла.

Для степени с действительным показателем сохраняются все известные свойства степени с рациональным показателем, из которых следует теорема.

Теорема. Пусть 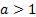и 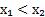. Тогда .

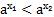Доказательство:

По условию 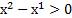. Поэтому, по свойству 1 имеем
а^(х₂ ) 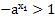. Умножив обе части этого равенства на положительное число 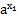, получим 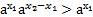. По свойству умножения степеней получаем: 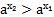, т. е. .

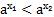Из данной теоремы вытекают три следствия:

1. Пусть 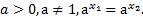Тогда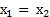

2. Пусть 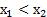и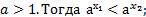

.

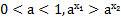1. Пусть 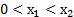и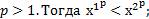

.

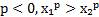Эти теорема и следствия помогают при решении уравнений и неравенств, сравнении чисел.

⇐ Предыдущая 123 Следующая ⇒

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.