Хелпикс

Главная

Контакты

Случайная статья



Степень с рациональным и действительным показателем.

Стр 1 из 3Следующая ⇒


Если n- натуральное число, 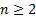, m- целое число и частное 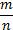является целым числом, то при 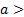0 справедливо равенство:

.

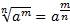Напомним, что r-рациональное число вида 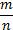, где m- целое число, n- натуральное число. Тогда по нашей формуле получим:

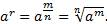
Таким образом, степень определена для любого рационального показателя r и любого положительного основания а.

Если 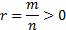, то выражение 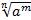имеет смысл не только при 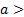0, но и при а=0, причем, 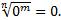Поэтому считают, что при r 0 выполняется равенство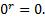

Пользуясь формулой 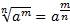степень с рациональным показателем можно представить в виде корня и наоборот.

Рассмотрим несколько примеров:

1.

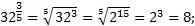
2.

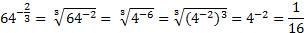
Отметим, что все свойства степени с натуральным показателем, которые мы с вами повторили, верны для степени с любым рациональным показателем и положительным основанием, а именно, для любых рациональных чисел p и q и любых 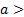0 и 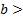0 ы следующие равенства:

1. ;

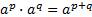2. ;

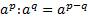3.

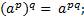
4.

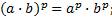
5.

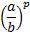
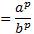
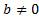
Разберем несколько примеров, воспользовавшись данными свойствами:

1. Вычислим: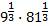

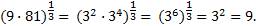
1. Упростить выражение:

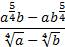
В числителе вынесем общий множитель ab за скобки, в знаменателе представим корни в виде дробных показателей степени:

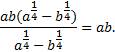
А теперь дадим определение степени с действительным показателем, на примере .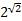

Пусть последовательность десятичных приближений с недостатком :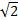

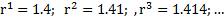
Эта последовательность стремится к числу 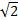, т. е.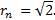

Числа являются рациональными, и для них определены степени 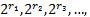т. е. определена последовательность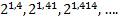

Можно сделать вывод, что данная последовательность стремится к некоторому действительному числу, которое обозначают 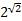, т. е. .


123Следующая ⇒
  

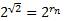© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.