Доказательство.. Доказательство.

Доказательство.

Пусть α и β — параллельные плоскости, а γ — плоскость, пересекающая их.

Плоскость α пересекается с плоскостью γ по прямой a.

Плоскость β пересекается с плоскостью γ по прямой b.

Линии пересечения a и b лежат в одной плоскости γ и потому могут быть либо пересекающимися, либо параллельными прямыми. Но, принадлежа двум параллельным плоскостям, они не могут иметь общих точек. Следовательно, они параллельны.

Теорема 2. Отрезки параллельных прямых, заключённых между двумя параллельными плоскостями, равны.

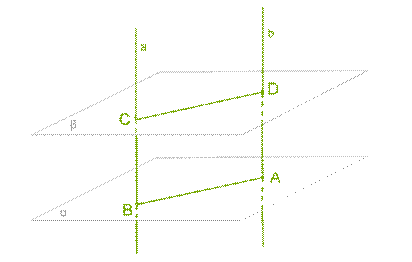
Рис. 4. Параллельные прямые пересекают две параллельные плоскости.

Доказательство.

Пусть α и β — параллельные плоскости, а a и b — параллельные прямые, пересекающие их.

Через прямые a и b можно провести плоскость — эти прямые параллельны, значит, определяют плоскость, причём только одну.

Проведённая плоскость пересекается с плоскостью α по прямой AB, а с плоскостью β — по прямой CD.

По предыдущей теореме прямые AB и CD параллельны. Четырёхугольник ABCD есть параллелограмм (у него противоположные стороны параллельны). А раз это параллелограмм, то противоположные стороны у него равны, то есть BC=AD.

⇐ Предыдущая 12