
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
График функции у = arсcоs x
05. 02. 2022г.
Задание высылать не позднее 16: 00 06. 02. 2022г в личном сообщении в вк или на почту SHPAK. IRINA. S@yandex. ru
Перед каждым заданием в тетради пишем ФИО, дата, тема урока
Тема урока: « Обратные тригонометрические функции».
График функции у = arcsinx
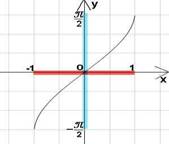 - Назовите основные свойства функции, обратной у=sinx.
- Назовите основные свойства функции, обратной у=sinx.
( Свойства функции у = arcsinx.
· Область определения функции  .
.
· Область значений функции ): 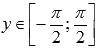 .
.
· Функция нечетная, так как 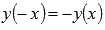 .
.
· Функция возрастает на всей области определения, то есть, при  .
.
· Функция вогнутая при 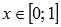 , выпуклая при
, выпуклая при 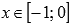 .
.
· Точка перегиба (0; 0), она же ноль функции.
· Асимптот нет. )
- Определите алгоритм построения графика функции, обратной y=cosx.
( Необходимо установить главную ветвь косинуса).
- Предположите, какой промежуток из области определения можно рассмотреть как главную ветвь косинуса?
( [0; 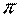 ] – главная ветвь косинуса. )
] – главная ветвь косинуса. )
- Каковы будут следующие этапы?
(- Провести ось симметрии у = х.
- Отобразить точки главной ветви косинуса относительно оси.
- Выполнить построение. )
- По алгоритму постройте график функции, обратной y=cosx.
(Демонстрация работ)

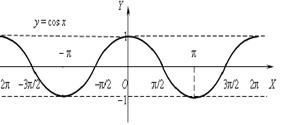
Главная ветвь косинуса
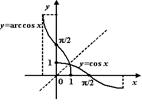
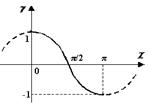
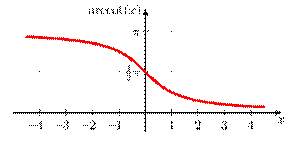
График функции у = arсcоs x
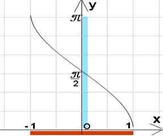
- Итак, функция у=cosx в промежутке [0; 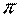 ] имеет обратную функцию, она называется арккосинусом и обозначается у = arccоsx .
] имеет обратную функцию, она называется арккосинусом и обозначается у = arccоsx .
Назовите основные свойства функции.
( Свойства функции у = arccоsx:
-Область определения функции:  .
.
· Область значений функции ): 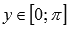 .
.
· Функция не является ни четной ни нечетной, то есть, она общего вида.
· Функция убывает на всей области определения, то есть, при  .
.
· Функция вогнутая при 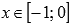 , выпуклая при
, выпуклая при 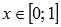 .
.
· Точка перегиба 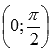 .
.
· Асимптот нет. )
Информация о домашнем задании.
- Как вы считаете, полностью ли мы выполнили цель урока? (Нет, не рассмотрели графики функций, обратных y=tgx и y=ctgx. )
- Таким образом, сформулируйте домашнее задание.
( Выполнить построение графиков функций, обратных y=tgx и y=ctgx. )
Домашнее задание:
- Составить алгоритм построения графиков функций, обратных y=tgx и y=ctgx.
- Выполнить построение графиков функций, обратных y=tgx и y=ctgx.
- Выписать свойства функций, обратных y=tgx и y=ctgx.
ПРИЛОЖЕНИЯ
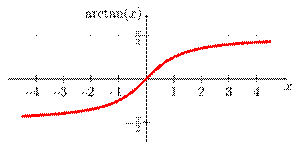
Свойства функции арктангенс y = arctg(x).
· Область определения функции : : 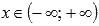 .
.
· Область значений функции арктангенс:  .
.
· Функция нечетная, так как 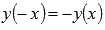 .
.
· Функция возрастает на всей области определения, то есть, при 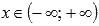 .
.
· Функция вогнутая при 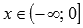 , выпуклая при
, выпуклая при 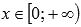 .
.
· Точка перегиба (0; 0), она же ноль функции.
· Горизонтальными асимптотами являются прямые 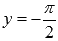 при
при 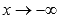 и
и 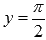 при
при 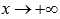 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|