- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
В 12. мирегэ.ру. 1. Из пункта А в пункт В вниз по течению реки отправились одновременно моторная лодка и байдарка. Скорость течения реки равна 3 км/ч. Последнюю часть пути моторная лодка шла с выключенным мотором, и её скорость относительно берега была ра
В 12. мирегэ. ру
Задачи на движение по воде.
1. Из пункта А в пункт В вниз по течению реки отправились одновременно моторная лодка и байдарка. Скорость течения реки равна 3 км/ч. Последнюю часть пути моторная лодка шла с выключенным мотором, и её скорость относительно берега была равна скорости течения. На той части пути, где моторная лодка шла с включённым мотором, её скорость была на 2 км/ч больше скорости байдарки. Найдите скорость байдарки в неподвижной воде, если в пункт В байдарка и моторная лодка прибыли одновременно.
Решение:
Пусть х км/ч - скорость байдарки.
| v(км/ч) |
t(ч) | S(км) | ||
| Моторная лодка | х+5 | 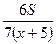
| 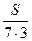
| s |
| Байдарка | х+3 | | s | |
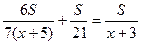 разделим на S.
разделим на S.
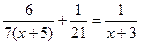 НОЗ=21(Х+5)(Х+3)
НОЗ=21(Х+5)(Х+3)
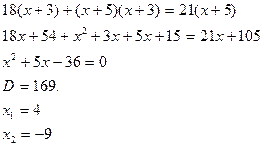
(не удовлетворяет условиям задачи)
Ответ: скорость байдарки 4 км/ч.
2. Катер, собственная скорость которого равна 15 км/ч, прошел 60 км по реке от данной пристани до другой и вернулся обратно. За это же время спасательный круг, упавший за борт с катера, проплывает 25 км. Найдите время движения катера вверх по реке.
Решение:
В данной задаче основные скорости – собственная скорость катера, равная 15 км/ч, и скорость течения, которая не дана. Обозначим скорость течения за x км/ч.
Тогда на путь по течению катер со скоростью (15+x) км/ч затратил 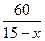 ч, а на путь против течения катер со скоростью (15-x) км/ч затратил
ч, а на путь против течения катер со скоростью (15-x) км/ч затратил 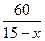 ч.
ч.
Спасательный круг проплывает 25 км по течению реки за 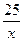 км/ч. Учитывая, что по условию задачи на путь туда и обратно катер затратил такое же время, за какое спасательный круг проплывает 25 км, составим уравнение:
км/ч. Учитывая, что по условию задачи на путь туда и обратно катер затратил такое же время, за какое спасательный круг проплывает 25 км, составим уравнение:
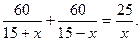
Для упрощения вычислений разделим обе части уравнения на 5 и получим
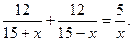
Так как по условию задачи 0< x< 15, то есть знаменатели всех дробей в уравнении отличны от нуля, умножим обе части уравнения на (15+x)(15-x)x и получим уравнение, равносильное данному:
(12(15-x)+12(15+x))x=5(15+x)(15-x).
Приведем полученное уравнение к квадратичному:
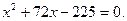
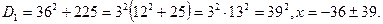
Уравнение имеет единственный положительный корень x=3, отрицательный корень не удовлетворяет условию задачи.
Итак, скорость течения реки равна 3 км/ч. Далее узнаем время движения вверх по реке:
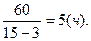
Ответ: 5.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|