По Белокуровой Е.Е.. Таблицы. По Истоминой Н.Б.

По Белокуровой Е. Е.

Автор рассказывает, о том что на комбинаторных задачах идёт обучение методу перебора. Комбинаторные задачи используют для развития вариативности мышления.

Задачи, которые решают методом перебора делят на 3 вида:

1. Задачи, с полным перебором вариантов.

2. Задачи, в которых использовать прием полного перебора не целесообразно и нужно сразу исключить некоторые варианты не рассматривая их.

3. Задачи, в которых метод перебора производится несколько раз и по отношению разного рода объектам.

Таблицы

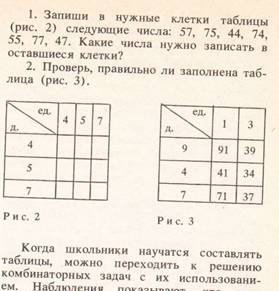
Графы

По Истоминой Н. Б.

Методика обучения решению комбинаторных задач разрабатывалась в рамках методической системы развивающего обучения младших школьников математике (Н. Б. Истомина), которая выражает необходимость целенаправленного и систематического формирования приемов умственной деятельности в процессе усвоения математического содержания.

Нацеленность начального курса математики на формирование приемов умственной деятельности позволяет установить внутреннюю связь между развивающими условиями обучения и способами их достижения, так как в процессе усвоения знаний, умений и навыков приемы умственной деятельности выполняют различные функции и их можно рассматривать:

1) как способ организации учебной деятельности школьников;

2) как способы познания, которые становятся достоянием ребенка, характеризуя его интеллектуальный потенциал и способности к усвоению знаний;

3) как способы включения в процесс познания различных психических функций: эмоций, воли, чувств, внимания; в результате интеллектуальная деятельность ребенка входит в различные соотношения с другими сторонами его личности, прежде всего с ее направленностью, мотивацией, интересами, уровнем притязаний т. е. характеризуется возрастающей активностью личности в различных сферах ее деятельности.

Средствами реализации данной концепции являются:

– тематическое построение курса, создающее условия для осознания школьниками связей между новыми и ранее изученными понятиями, для осуществления продуктивного повторения, для активного использования в процессе обучения приемов умственной деятельности;

– новый методический подход к изучению математических понятий, свойств и способов действий, в основе которых лежит установление соответствия между предметными, графическими (схематическими) и символическими моделями, их выбор, преобразование и конструирование в соответствии с заданными условиями;

– новый методический подход к формированию вычислительных навыков и умений, который создает условия не только для повышения качества вычислительной деятельности младших школьников, но и для развития их мышления;

– новый методический подход к обучению младших школьников решению текстовых задач, в соответствии с которым дети знакомятся с текстовой задачей только после того, как у них сформированы те знания, умения и навыки (навыки чтения, усвоение конкретного смысла сложения и вычитания, приобретение опыта в соотнесении предметных, словесных, схематических и символических моделей, знакомство со схемой как способом моделирования), которые необходимы им для овладения умением решать текстовые задачи;

– включение в учебник диалогов между Мишей и Машей, с помощью которых детям предлагаются для обсуждения варианты ответов, высказываются различные точки зрения, комментируются способы математических действий, анализируются ошибки. Диалоги помогают учителю не только привлечь учащихся к обсуждению того или иного вопроса, но и самому включиться в эту работу, заняв тем самым позицию не контролирующего, а помогающего детям и сотрудничающего с ним.

Органически вписываясь в логику построения содержания курса, в методику обучения решению задач, в систему учебных заданий, в процессе выполнения которых учащиеся усваивают знания, умения и навыки, комбинаторные задачи выступают как одно из средств реализации методической концепции развивающего обучения младших школьников математике.

Возможность данного положения обусловливается спецификой комбинаторных задач, решение которых требует активного использования таких приемов умственной деятельности как анализ и синтез, сравнение, классификация, обобщение.

Методика обучения решению комбинаторных задач находится в соответствии с методическим подходом к формированию у младших школьников математических понятий, который связан с установлением соответствия между различными моделями. Возможность такого соответствия определяется способами решения комбинаторных задач. Так способ перебора (хаотичного и системного) позволяет детям решать комбинаторные задачи, опираясь на имеющийся у них опыт, на предметно-действенное и наглядно-образное мышление.

Используя для решения комбинаторных задач таблицы и графы, учащиеся фактически переводят вербальные модели в схематические. Тем самым у них формируются представления о моделировании как способа решения задач.

⇐ Предыдущая 1 23