Контакты

Случайная статья

Задача 2.

⇐ ПредыдущаяСтр 2 из 2

Задача 2.

В правильной треугольной призме 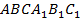, все ребра которой равны 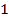, найдите косинус угла между прямым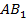и и 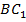. (См. Рис. 13. )

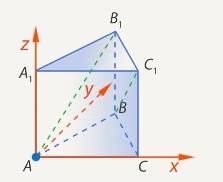
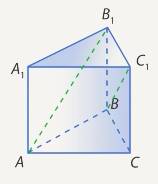
Рис. 13. Иллюстрация к задаче

Решение. 1. Введем систему координат. (См. Рис. 14. )

Рис. 14. Ввели систему координат

Если сделать выносной рисунок основания призмы, получим уже понятный плоскостной рисунок. (См. Рис. 15. ) Тогда мы сможем найти координаты всех интересующих нас точек.

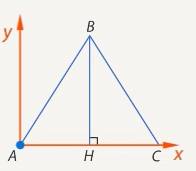
Рис. 15. Выносной рисунок основания призмы

Точка 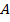имеет координаты 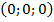. Точка 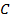– 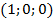. Точка – .

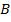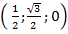Тогда точка 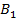имеет координаты 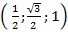, а точка – .

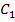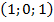2. Найдем координаты векторов 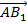и :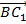

, .

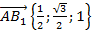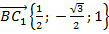3. Найдем длины векторов 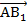и :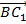

.

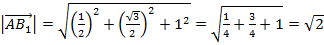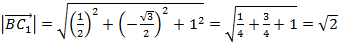
4. Найдем скалярное произведение векторов 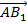и :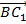

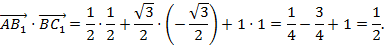
5. Найдем косинус угла между прямым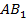и и :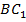

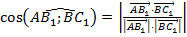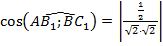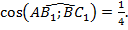, , Ответ: .

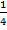Пример 3. Найти угол 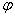между векторам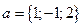и и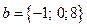
Решение: Применим формулу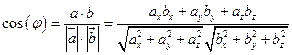

Подставим

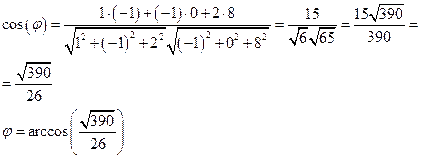Ответ: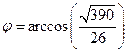

⇐ Предыдущая 12

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.