
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема. Решение математических и прикладных задач
Занятие по математике №101 № п/п-6 Группа 1ВГ Дата проведения: 16. 06. 21г.
Тема. Решение математических и прикладных задач
Выполненные задания отправлять на электронную почту: tatiefremenko@yandex. ua
или страницу вКОНТАКТЕ - https: //vk. com/id592773352
Индивидуальные консультации, оценивание устных ответов по тел.:
0660627421, 0721813966 Ефременко Т. А.
Видеофильм данной темы просмотреть по ссылке:
https: //www. youtube. com/watch? v=i0DXRtNdug8
Домашнее задание: прочитать §2, п. 51, стр. 113, «Геометрия 10-11 класс», Л. С. Атанасян, выучить определения, формулы, рассмотреть примеры решения задач и записать их в рабочую тетрадь.
Учебный материал для самостоятельного изучения
Задача 1. В единичном кубе 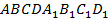 найти угол между прямыми
найти угол между прямыми 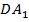 и
и 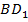 . (См. Рис. 9. )
. (См. Рис. 9. ) 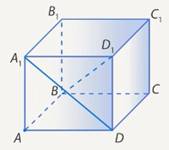
Рис. 9. Иллюстрация к условию
Решение. Сразу отметим, что требуется найти угол между прямыми, то есть угол между ними будет острым. Значит, если косинус получится отрицательным, то надо взять его по модулю, найдя смежный острый угол.
Способ 1. Введем систему координат. (См. Рис. 10. )
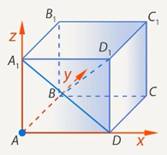 Рис. 10. Ввели систему координат
Рис. 10. Ввели систему координат
Найдем координаты интересующих нас точек: 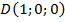 ,
, 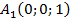 ,
, 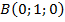 ,
, 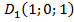 .
.
Теперь найдем координаты векторов: 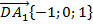 ,
, 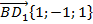 .
.
Тогда нужно найти косинус угла между данными векторами: 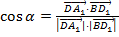 . Тогда
. Тогда 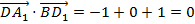 .
.
Значит, 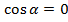 . Тогда эти векторы перпендикулярны, а тогда и угол между исходными прямыми – прямой, то есть
. Тогда эти векторы перпендикулярны, а тогда и угол между исходными прямыми – прямой, то есть 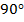 .
.
Способ 2. Перенесем вектор 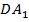 параллельно так, чтобы точка
параллельно так, чтобы точка 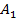 совместилась с точкой
совместилась с точкой 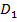 , получим вектор
, получим вектор 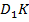 , тогда найдем угол между
, тогда найдем угол между 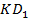 и
и 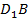 . (См. Рис. 11. )
. (См. Рис. 11. )
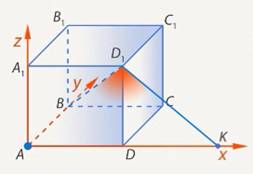
Рис. 11. Иллюстрация ко второму способу решения
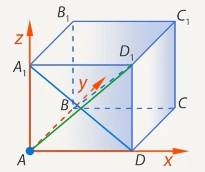 Способ 3. Используем теорему о трех перпендикулярах. Проекцией прямой
Способ 3. Используем теорему о трех перпендикулярах. Проекцией прямой 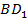 на плоскость передней грани является прямая
на плоскость передней грани является прямая 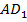 , которая перпендикулярна
, которая перпендикулярна 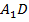 (как диагональ квадрата). (См. Рис. 12. ) Значит, исходные прямые перпендикулярны.
(как диагональ квадрата). (См. Рис. 12. ) Значит, исходные прямые перпендикулярны.
Рис. 12. Прямая 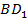 и ее проекция
и ее проекция 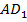
Ответ: 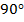 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|