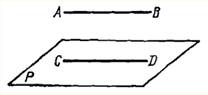
Если прямая АВ параллельна к прямой СD, которая лежит в плоскости Р, то она параллельная к плоскости Р.

Если прямая АВ параллельна к прямой СD, которая лежит в плоскости Р, то она параллельная к плоскости Р.

Если две плоскости Р и Q, что проходят соответственно через параллельные прямые АВ и СD, пересекаются, то линия их пересечения МN параллельна до обоих данных прямых АВ и СD.

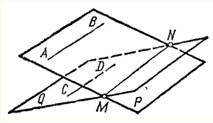
Две прямые, параллельные к одной и той же третьей прямой, параллельны между собой.

Если плоскость проходит через прямую, параллельную к другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна к данной прямой.

Если прямая параллельна к каждой из двух плоскостей, которые пересекаются, то она параллельна к линии их пересечения.

Если одна из двух параллельных прямых параллельная к некоторой плоскости, то и вторая прямая параллельная к той же плоскости или лежит в ней.

Через каждую из двух скрещивающихся прямых проходит плоскость, и к тому же только одна, параллельная к другой прямой.

Закрепление нового материала.

Тест

Вопрос 1. Сколько существует случаев взаимного расположения двух различных прямых в пространстве?

а) 2 б) 3 в) 1

Вопрос 2. В тексте дано определение скрещивающихся прямых. Правильно ли следующее определение: " Две прямые называются cкрещивающимися, если не существует плоскости, в которой лежат обе эти прямые".

а) нет б) да в) ответить однозначно нельзя

Вопрос 3. Сколько существует случаев взаимного расположения плоскостей?

а) 2 б) 3 в) 1

Вопрос 4. Сколько пар параллельных плоскостей имеет куб?

а) 1 б) 2 в) 3

Вопрос 5. Сколько случаев взаимного расположения прямой и плоскости?

а) 2 б) множество в) 3

Вопрос 6. Что необходимо для того, чтобы прямая и плоскость были перпендикулярны?

Вопрос 7. Что необходимо для того, чтобы две плоскости были параллельны?

Вопрос 8. Две прямые в пространстве называются параллельными, если они принадлежат одной плоскости и не имеют общих точек. Верно ли утверждение?

а) да б) нет

Задание на дом: Конспект, тест и № 121, 125.
№121

В треугольнике ABC дано: ∠ C = 90°, AC = 6 см, ВС = 8 см, СМ — медиана. Через вершину С проведена прямая СК, перпендикулярная к плоскости треугольника ABC, причем СК = 12 см. Найдите КМ.

№125

Через точки Р и Q прямой PQ проведены прямые, перпендикулярные к плоскости α и пересекающие ее соответственно в точках Р1 и Q1. Найдите P1Q1, если PQ = 15 см, РР1 = — 21, 5 см, QQ1=33, 5 см.

⇐ Предыдущая 12