Т. 6 Зн.5 Лінійнедифер. р-нняпершого порядку.

Т. 6 Зн. 5 Лінійнедифер. р-нняпершого порядку.

Р-ння виду 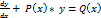Назив. лінійним неоднорідним диф. рівнянням 1-го продяку зі змінними коеф. Подамо невідому функцію у вигляді добутку двох довільних функцій U(x) та V(x), y(x) = U(x) * V(x)
тоді 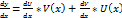підставиво ці вирази в початкове р-ння, (*) Оскільки функція V(x) довільна, то виберемоїї так, щобвираз в дужках дорівнював 0 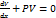, , 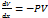, , 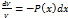, 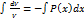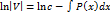), , 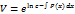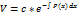. Внаслідок довільності функції Vвиберемо с=1
Тоді V= 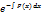Підставимо знайдену функцію V, в рівняння *
Отримаємо, , , , .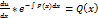
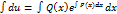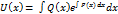Оскільки y(x) = U(x)*V(x), то загальний розв’язок лінійного рівняння має вигляд: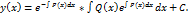

Т. 6 Зн. 7 Диферрівняння другого порядку.
Рівняння виду ay``+by`+cy=0 називдифер. Рівнянням 2-го порядку з сталими коеф. Очевилно, що залежність функції у можна підставити функцію y=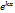

y` = k* 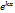, y`` = 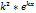, a 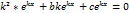, , 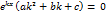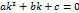. Це рівняння назив характеристичним рівнянням даного дифер рівняння Розв’язавши його отримаємо 2 значення k 1 випадок:
D> 0 => k1 недорівнюєk2 є R Вцьомувипадкузагрозв’язок однорідного диф рівняння 2-го порядку записується у вигляді: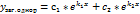

2випадок: D=0 k1 = k2 = k є R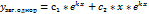

3 випадок: D< 0 квадратичнерівняннямає 2 комплексно-спряжених розв’язки k1, 2 =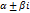

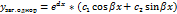
Т. 6 Зн. 8 Розв’язання лінійних диферрівнянь зі сталими коеф.

Розв’язок лінійного неоднорідного дифер рівняння зі сталими коеф.

ay``+by`+cy = f(x) подається у вигляді суми загал. розв’язку відповідного однорідного рівняння та деякого частинного розв’язку неоднорідного 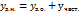Частинний розв’язок Учн. подається у вигляді неоднорідності f(x).
1) якщо неоднорыдныстьf(x) має показникові форму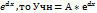
2) якщо f(x) = Pn(x), то Учн. = Qn(x), де Pn(x)-многочлен n-го степеня Qn(x) тежмногочл. n-гостепеня з невідомими коеф. 3) якщо f(x) = acosx +bsinx
то Учн. =Acosx + Bsinx 4)Взаг. випадку, якщоf(x) = Pn(x) * 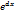, то Учн. = 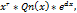де r – кратныстькореня α в характеристичному рівнянні Qn(x) –многочлен n-го степеня з невизначеними коеф. Якщо число α не є коренем характер ест. рівн, то r = 0 і Учн. = 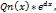Для знах. невизначених коеф. у частинному розв’язку знаходять всі похідні Учн. і підставивши їх в неоднорідне рівняння, прирівнюємо відповідні коеф. Внаслідок цього отримаємо одне або систему рівнянь звідки знаходимо невизначені коеф. частинного розв’язку і підставивши їх в Учн. , записуємо заг. розв’язок неоднорідного рівняння. Якщо права частина ЛДР з сталим коеф. має вигляд 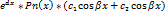та його частинний розв'язок шукаємо у вигляді Учн. = 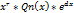*( 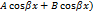Z=α +β i

де r- кратність кореня в характеристичному рівнянні.

⇐ Предыдущая 12