
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Т.6 Зн.3 Однорідні дифер.рівняння першого порядку.
Т1. З1. Матриці. Матрицею наз. прямокутна табличка елементів (чисел). Якщо матриця містить m рядків і n стовпців то кажуть що дана матриця має розмірність m*n. Елементи матриці познач. aij, де i- номер рядка j- номер стовбця в якому знах. Елемент. Таким чином матриця А розмірності m*n має вигляд Аm*n= 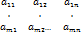 якщо кількість рядків = кількості стовбців, то матриця наз. квадратного розмірності n або n-го порядку.
якщо кількість рядків = кількості стовбців, то матриця наз. квадратного розмірності n або n-го порядку.
Дії над матрицею. Додавання. Сумою двох матриць однакових розмірностей Аm*n і Вm*n є матриця С тієї ж розмірності, елементи якої є сумою відповідних елементів матриць А і В. А+В=С, cij=aij+bij.
Різниця. А-В=С, cij=aij-bij.
Множення матриці на скаляр. Для того щоб помножити матрицю на число … потрібно на це число помножити кожен елемент матриці. λ А=(λ aij)
Множення матриць. Матриці А і В наз. узгодженими, якщо вони мають розмірності m*l та l*m. Добуток двох матриць Аm*l і Вl*m є матриця Сm*n, ij-й елемент якої = скалярному добутку і-го рядка матриці А та j-го стовбця матриці В. множення матриць операція не комутативна А*В 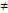 В*А.
В*А.
Визначники. Кожній квадратній матриці можна поставити у відповідність певне число яке наз визначником, або детермінантом цієї матриці і познач ∆ або ∆ А, 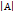 , det A. Детермінантом квадратної матриці наз сума добутків її елементів взятих по одному і тільки одному з кожного рядка і стовбця з певним знаком. Детермінантом квадратної матриці другого порядку
, det A. Детермінантом квадратної матриці наз сума добутків її елементів взятих по одному і тільки одному з кожного рядка і стовбця з певним знаком. Детермінантом квадратної матриці другого порядку  наз число …= а11а12-а12а21. Елементи а11,
наз число …= а11а12-а12а21. Елементи а11,  , …, аnnназ головною діагоналю квадратної матриці. Друга діагональ наз допоміжною. Детермінантом квадратної матриці а 3*3
, …, аnnназ головною діагоналю квадратної матриці. Друга діагональ наз допоміжною. Детермінантом квадратної матриці а 3*3  наз число ∆ = а11а22а33+а12а23а31+а13а21а32-а13а22а31-а12а21а33-а11а23а32
наз число ∆ = а11а22а33+а12а23а31+а13а21а32-а13а22а31-а12а21а33-а11а23а32
Правило трикутника. Елементи головної діагоналі та рівнобедрених трикутників з основами паралельними до неї входять в детермінант 3*3 зі знаком +, елементи допоміжної діагоналі і рівнобедрених трикутників з паралельними до неї основами -. 

Правило допоміжних стовпців. З права від детермінанта дописуємо два його перші стовбці. Добуток елементів головної діагоналі та відрізків, паралельних до неї входять в детермінант зі зміним знаком + допоміжна діагональ та відрізки паралельні до неї зі знаком -. 

СЛАР. (СИСТЕМА ЛІНІЙНИХ АЛГЕБРАЇЧНИХ РІВНЯНЬ)
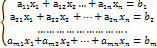 квадратна матриця головна діагональ якої складається з одиниць а інші елементи =0 наз одиничною матрицею і познач Е Е=
квадратна матриця головна діагональ якої складається з одиниць а інші елементи =0 наз одиничною матрицею і познач Е Е= 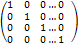
Т2. З2. Методи знаходження оберненої матриці. Нехай дано детермінант n-го порядку з елементами aij. Мінором елемента aij наз детермінант 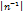 -го утворений ви кресленням і-го рядка та j-го стовбця початкового детермінанта. ∆
-го утворений ви кресленням і-го рядка та j-го стовбця початкового детермінанта. ∆  n*n Mij=
n*n Mij=  (n-1)*(n-1). Алгебраїчним доповненням елемента
(n-1)*(n-1). Алгебраїчним доповненням елемента 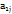 наз М цього елемента взятий з відповідним знаком. Аij=(-1)i+j*mij. . Матриця АТm*nутворена з матриці Аm*nзамінною рядків на стовбців наз транспонованою матрицею. А=
наз М цього елемента взятий з відповідним знаком. Аij=(-1)i+j*mij. . Матриця АТm*nутворена з матриці Аm*nзамінною рядків на стовбців наз транспонованою матрицею. А=  АТ=
АТ=  . Матриця А-1 наз оберненою до матриці А якщо А*А-1= А-1* А=Е. Висновок: 1. Обернені матриці можна шукати тільки для квадратних матриць. 2. Обернені матриці шукаються тільки для тих det яких не рівний. Способи знаходження А-1: метод алгебраїчних доповнень
. Матриця А-1 наз оберненою до матриці А якщо А*А-1= А-1* А=Е. Висновок: 1. Обернені матриці можна шукати тільки для квадратних матриць. 2. Обернені матриці шукаються тільки для тих det яких не рівний. Способи знаходження А-1: метод алгебраїчних доповнень 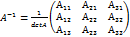 ,
,
А-1= 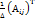
Т1. З4. Дії над матрицями. Рівносильними перетвореннями матриці наз множення будь-якого рядка на відмінний від 0 число та додавання будь-яких двох рядків. Теж саме можна робити зі стовбцями матриці. Матриця всі елементи якої під елементами а11, а22, і тд = 0 наз матрицею трикутного вигляду. За допомогою рівносильних перетворень будь-яку матрицю можна звести до трикутного вигляду. Квадратна матриця має діагональний вигляд якщо елементи крім елементів головної діагоналі = 0. Рангом матриці А розмірність найбільшого не нульового мінора цієї матриці. Ранг матриці = кількості не нульових рядків після зведення матриці до трикутного вигляду.
Т1. З5. Обчислення визначників. Властивості визначників. 1. Якщо det містить нульовий рядок або стовбець то він = 0. 2. Якщо детермінант містить два однакові рядки або стовбці то він = 0. 3. Якщо один з рядків або стовбців det є лінійною комбінацією кількох інших то він = 0. 4. Якщо транспонувати детермінант то його значення не зміниться. 5. Якщо поміняти місцями два рядки або стовбці det то він змінить знак. 6. Якщо всі елементи det під головною діагоналлю = 0 то det = добутку діагональних елементів. 7. Теорема П'єра-Сімона Лапласа (розклад det за елементами рядка або стовбця ) det n-го порядку = сумі добутків елементів і-го рядка (або j-го стовбця) на їх алгебраїчні доповнення. ∆ = 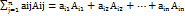 (сума по j від 1 до n aij на Aij).
(сума по j від 1 до n aij на Aij).
Т1. З6. СЛАР. Методи розв’язання. Нехай задано систему m алгебраїчних рівнянь з невідомими. 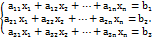 Матриця А=
Матриця А=  m*n наз основною матрицею. Матриця А|В=
m*n наз основною матрицею. Матриця А|В= 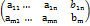 m*(n+1) наз розширеною матрицею системи рівнянь. Матриця В =
m*(n+1) наз розширеною матрицею системи рівнянь. Матриця В = 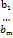 наз стовбчиком вільних членів. Матриця Х=
наз стовбчиком вільних членів. Матриця Х= 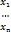 наз матрицею невідомих. Систему СЛАР можна записати в матричному вигляді. А*Х=В СЛАР наз визначеною якщо вона має єдиний розв’язок. СЛАР нез невизначеною якщо вона має безліч розв’язків. Якщо СЛАР не має розв’язків то вона наз несумісною системою. Теорема Кронеккера-Капелі. 1. Якщо rang основної матриці = rang розширеною і = кількості невідомих то система визначена. 2. Якщо rang основної матриці = rang розширеної але менший за кількість невідомих то система невизначена. 3. Якщо rang основної матриці менший за rang розширеної то вона не сумісна. Якщо СЛАР склад з n рівнянь з n невідомими і det основної матриці не рівний 0 то система і її розвязок можна знайти за формулою Крамера. Методи розв’язання СЛАР: 1. формули Крамера
наз матрицею невідомих. Систему СЛАР можна записати в матричному вигляді. А*Х=В СЛАР наз визначеною якщо вона має єдиний розв’язок. СЛАР нез невизначеною якщо вона має безліч розв’язків. Якщо СЛАР не має розв’язків то вона наз несумісною системою. Теорема Кронеккера-Капелі. 1. Якщо rang основної матриці = rang розширеною і = кількості невідомих то система визначена. 2. Якщо rang основної матриці = rang розширеної але менший за кількість невідомих то система невизначена. 3. Якщо rang основної матриці менший за rang розширеної то вона не сумісна. Якщо СЛАР склад з n рівнянь з n невідомими і det основної матриці не рівний 0 то система і її розвязок можна знайти за формулою Крамера. Методи розв’язання СЛАР: 1. формули Крамера 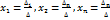 де ∆ - det основної матриці, ∆ j- det основної матриці в якій j-ий стовбець замінений стовпчиком вільних членів. 2. Метод Гауса. За допомогою рівносильних перетворень звидим розширену матрицю систем до трикутного вигляду. З останнього рівняння перетвореної матриці знаходимо або виражаємо останню невідому. Підставивши це значення в передостаннє рівняння знаходимо значення передостанньої зміни і тд поки не знайдемо всі невідомі. 3. Матричний метод. Записуємо СЛАР в матричному вигляді: АХ=В, А-1АХ=А-1В, ЕХ=А-1В, Х=А-1В.
де ∆ - det основної матриці, ∆ j- det основної матриці в якій j-ий стовбець замінений стовпчиком вільних членів. 2. Метод Гауса. За допомогою рівносильних перетворень звидим розширену матрицю систем до трикутного вигляду. З останнього рівняння перетвореної матриці знаходимо або виражаємо останню невідому. Підставивши це значення в передостаннє рівняння знаходимо значення передостанньої зміни і тд поки не знайдемо всі невідомі. 3. Матричний метод. Записуємо СЛАР в матричному вигляді: АХ=В, А-1АХ=А-1В, ЕХ=А-1В, Х=А-1В.
Т2. З1. Елементи векторної алгебри. Оскільки в математиці розгляд вільні вектори то співнаправлені вектори однакові довжини повинні мати рівні координати. Тому за координати вектора прийнято брати проекції цього вектора на координатні осі. мал. Якщо подивитися з будь-якої + точки на осі OZ на площину OXY то вісь OX повинна бути напрямлена вправо тому горизонтальна віс, ординат (OY) третя вісь абсцис (Х). на цьому зображенні проекціями вектора  на осі є числа ах, ау, аzтому
на осі є числа ах, ау, аzтому 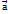 має координати:
має координати: 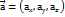 . Очевидно що у випадку коли вектора
. Очевидно що у випадку коли вектора  задано двома точками М1=(х1; у1; z1)- початком М2=(х2; у2; z2)- кінцем то для того щоб знайти координат вектора
задано двома точками М1=(х1; у1; z1)- початком М2=(х2; у2; z2)- кінцем то для того щоб знайти координат вектора 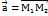 потрібно від координат кінця відняти відповідні координати початку: ах=х2-х1 ау= у2-у1 аz=z2-z1. Положення вектора у просторі також може бути задане чотирма числами довжиною цього вектора і трьома cos кутів яку утвор цей вектор з додатними напрямками осей координат. Якщо вектор
потрібно від координат кінця відняти відповідні координати початку: ах=х2-х1 ау= у2-у1 аz=z2-z1. Положення вектора у просторі також може бути задане чотирма числами довжиною цього вектора і трьома cos кутів яку утвор цей вектор з додатними напрямками осей координат. Якщо вектор  задано своїми координатами
задано своїми координатами 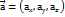 то його модуль (довжина) обчислюється за формулою: :
то його модуль (довжина) обчислюється за формулою: : 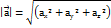 . Якщо вектор
. Якщо вектор  з віссю OX утвор кут … з віссю ОУ-β з віссю OZ-… то напрямлені косинуси знах з формули:
з віссю OX утвор кут … з віссю ОУ-β з віссю OZ-… то напрямлені косинуси знах з формули: 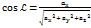 ,
, 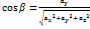 ,
, 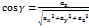 . Напрямлені косинуси вектора
. Напрямлені косинуси вектора 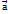 пов’язані між собою наступними співвідношенням. ОТТ:
пов’язані між собою наступними співвідношенням. ОТТ: 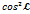 +
+ 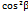 +
+ 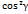 = 1. Дії над векторами: 1. Для того щоб помножити вектор на скляр потрібно на цей вектор помножити кожну координату вектора:
= 1. Дії над векторами: 1. Для того щоб помножити вектор на скляр потрібно на цей вектор помножити кожну координату вектора: 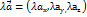 2. Сумою або різницею двох векторів є вектор координат якого є сумою або різницею відповідних координат заданих векторів:
2. Сумою або різницею двох векторів є вектор координат якого є сумою або різницею відповідних координат заданих векторів: 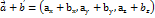 . 3. Скалярним добутком двох векторів наз число яке можна обчислити за двома формулами:
. 3. Скалярним добутком двох векторів наз число яке можна обчислити за двома формулами:
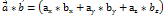 ;
; 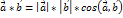 , використовуючи ці формули знах кут між двома векторами: cos𝝋 =
, використовуючи ці формули знах кут між двома векторами: cos𝝋 =  4. Векторним добутком двох векторів наз третій вектор одночасно перпендикулярний до даних двох векторів модуль якого знах за формулою:
4. Векторним добутком двох векторів наз третій вектор одночасно перпендикулярний до даних двох векторів модуль якого знах за формулою: 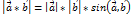 . Якщо скалярний добуток двох векторів від’ємний і кут також то кут буде тупий.
. Якщо скалярний добуток двох векторів від’ємний і кут також то кут буде тупий.
Т2. З2. Колінеарність. Два вектори наз колінеарними якщо вони лежать на одній або паралельних прямих. якщо напрямки колінеарних векторів співпадають вектори наз спів напрямленими, у іншому випадку протилежно напрямлені. Умова колінеарності векторів: 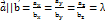 . При λ > 0 вектори
. При λ > 0 вектори 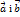 – співнапрямлені, λ < 0
– співнапрямлені, λ < 0 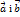 - протилежно напрямлені. Вектори
- протилежно напрямлені. Вектори 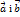 наз ортогональними якщо вони утвор кут 90 град. Умова ортогональності векторів:
наз ортогональними якщо вони утвор кут 90 град. Умова ортогональності векторів: 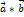 =0.
=0.
Т2. З3. Лінійні дії над векторами. Нехай задано два вектори 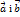 . Знайдемо проекцію вектора
. Знайдемо проекцію вектора 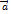 на проекцію вектор
на проекцію вектор 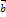 . З прямокутного трикутника маємо:
. З прямокутного трикутника маємо: 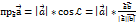 ,
, 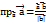 ,
, 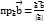 . Нехай вектор
. Нехай вектор  задано своїми координатами
задано своїми координатами 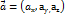 тоді цей вектор можна подати у вигляді
тоді цей вектор можна подати у вигляді 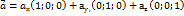 . Вектори
. Вектори 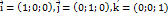 наз одиничними ортами. Таким чином кожен вектор
наз одиничними ортами. Таким чином кожен вектор  можна подати і вигляді
можна подати і вигляді 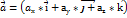 . Остання рівність наз розкладом вектора
. Остання рівність наз розкладом вектора  за базисними векторами
за базисними векторами 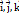 . Три вектора
. Три вектора 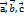 наз компленарними якщо вони лежать в одній площині. Якщо
наз компленарними якщо вони лежать в одній площині. Якщо 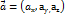 ,
, 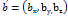 ,
, 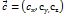 то умова компланарності цих векторів має вигляд: умова компланарності
то умова компланарності цих векторів має вигляд: умова компланарності 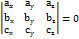 . Будь-які три на колінеарні вектори утворюють базис у тривимірному просторі. Три вектора
. Будь-які три на колінеарні вектори утворюють базис у тривимірному просторі. Три вектора 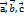 утвор базис тривимірного простору якщо будь-який четвертий вектор
утвор базис тривимірного простору якщо будь-який четвертий вектор 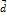 у цьому просторі можна подати у вигляді лінійної комбінації векторів
у цьому просторі можна подати у вигляді лінійної комбінації векторів 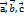 , тобто:
, тобто: 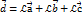 . Це означає що
. Це означає що 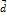 в системі координат
в системі координат 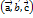 (
( 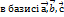 ) має координати
) має координати 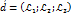
Т2. З4. Лінійні дії з векторами в координатах. Якщо 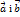 не колінеарні то на них як на двох сторонах можна побудувати паралелограм. Площа паралелограма = модулю векторного добутку цих векторів (векторів
не колінеарні то на них як на двох сторонах можна побудувати паралелограм. Площа паралелограма = модулю векторного добутку цих векторів (векторів 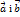 ).
). 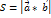 . векторний добуток знах за формулою:
. векторний добуток знах за формулою: 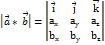 .
.
Т2. З5. Добуток векторів. 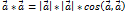 ,
, 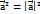 . скалярний квадрат вектора = квадрату його модуля.
. скалярний квадрат вектора = квадрату його модуля.
Т2. З7. Задачі на векторний добуток. 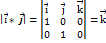 .
. 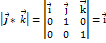 .
. 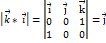 . Нехай задано три вектори
. Нехай задано три вектори 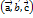 знайшовши векторний добуток
знайшовши векторний добуток 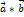 отримаємо новий вектор отриманий результат можна скалярно помножити на вектор
отримаємо новий вектор отриманий результат можна скалярно помножити на вектор  . Отримане число наз мішаним добутком
. Отримане число наз мішаним добутком 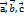 і познач:
і познач: 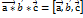 . На трьох не компленарних вектора
. На трьох не компленарних вектора 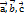 як на ребрах можна побудувати паралелепіпед об’єм якого = модулю мішаного добутку цих векторів. Vпар=
як на ребрах можна побудувати паралелепіпед об’єм якого = модулю мішаного добутку цих векторів. Vпар= 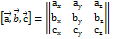 обєм структурної піраміди побудованої на ребрах
обєм структурної піраміди побудованої на ребрах 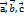 знах за формулою: VПІР=
знах за формулою: VПІР= 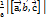 .
.
Т3. З1. Основи аналітичної геометрії. Рівняння прямої на площині: 1. Рівняння виду Ах+Вх+С=0(1) наз загальним рівнянням прямої. Якщо С=0 то пряма (1) проходить через початок координат. При А=0 отримуємо пряму паралельну осі ОХ. При В=0 отримуємо пряму паралельну осі ОУ. Вектор  перпендикулярний до прямої цієї прямої або просто нормалю. Якщо пряма записана аг рівнянням то її нормаль має координати:
перпендикулярний до прямої цієї прямої або просто нормалю. Якщо пряма записана аг рівнянням то її нормаль має координати: 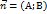 . 2. Рівняння прямої за двома точками (канонічне рівняння прямої)
. 2. Рівняння прямої за двома точками (канонічне рівняння прямої) 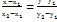 . 3. Вектор
. 3. Вектор 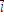 паралельний до прямої наз напрямленим вектором цієї прямої. Рівняння прямої за точкою і напрямленим відрізком.
паралельний до прямої наз напрямленим вектором цієї прямої. Рівняння прямої за точкою і напрямленим відрізком. 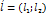 ,
, 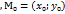 ,
, 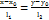 . 4. Рівняння прямої у відрізках. Якщо пряма відтинає на осі ОХ відрізок а, а на осі ОУ – відрізок b, то її рівняння має вигляд:
. 4. Рівняння прямої у відрізках. Якщо пряма відтинає на осі ОХ відрізок а, а на осі ОУ – відрізок b, то її рівняння має вигляд: 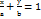 . 5. Нехай відоме відхилення прямої від початку координат (Р) і кут нахилу цього відхилення до додатного напрямку осі (ОХ) (𝝋 ) тоді рівняння прямої має вигляд: x*cos𝝋 +y*sin𝝋 -p=0. Нехай дано аг рівняння прямої. Тоді число μ = +
. 5. Нехай відоме відхилення прямої від початку координат (Р) і кут нахилу цього відхилення до додатного напрямку осі (ОХ) (𝝋 ) тоді рівняння прямої має вигляд: x*cos𝝋 +y*sin𝝋 -p=0. Нехай дано аг рівняння прямої. Тоді число μ = + 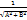 наз нормуючим множником (знак береться протилежний до знаку С). домножимо аг рівняння на μ. 6. Нормальне рівняння прямої.
наз нормуючим множником (знак береться протилежний до знаку С). домножимо аг рівняння на μ. 6. Нормальне рівняння прямої. 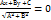 . Використовуючи нормальне рівняння прямої можна обчислити відстань від будь-якої точки до цієї прямої. Відстань від точки М (х0; ху) до прямої Ах+Вх+С=0 знах за формулою:
. Використовуючи нормальне рівняння прямої можна обчислити відстань від будь-якої точки до цієї прямої. Відстань від точки М (х0; ху) до прямої Ах+Вх+С=0 знах за формулою: 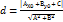 .
.
Т3. З2. Рівняння прямої і площини. Для того щоб записати вектор ортогональний до іншого двовимірного вектора потрібно координати цього вектора поміняти місцями і поміняти знак однієї координат.
Т3. З3. Метод координат. Якщо А(х1; у1), В(х2; у2) то координат точки М знах за формулою: 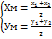 . Поділ відрізка у заданому відношенні А(х1; у1), В(х2; у2). Нехай точка М ділить відрізок АВ у відношенні λ тобто
. Поділ відрізка у заданому відношенні А(х1; у1), В(х2; у2). Нехай точка М ділить відрізок АВ у відношенні λ тобто 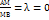 . Тоді координати точки М знах за формулою:
. Тоді координати точки М знах за формулою: 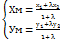 .
.
Т3. З5. Складання рівняння площини у просторі за даними умовами. Рівняння площини є умова компланарності векторів 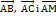 .
. 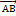 =(х2-х1; у2-у1; z2-z1),
=(х2-х1; у2-у1; z2-z1), 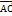 =(х3-х1; у3-у1; z3-z1),
=(х3-х1; у3-у1; z3-z1), 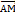 =(х-х1; у-у1; z-z1). 1. Рівняння площини за трьома точками:
=(х-х1; у-у1; z-z1). 1. Рівняння площини за трьома точками: 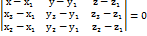 . 2. Загальне рівняння площини: АХ+ВУ+СZ+D=0,
. 2. Загальне рівняння площини: АХ+ВУ+СZ+D=0, 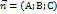 - нормальний вектор площини. 3. Якщо площина відтинає на осях координат відрізки а, b, с то її рівняння має вигляд:
- нормальний вектор площини. 3. Якщо площина відтинає на осях координат відрізки а, b, с то її рівняння має вигляд: 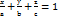 . Якщо площина відхилена від початку координат на відстань р і вектор
. Якщо площина відхилена від початку координат на відстань р і вектор  має напрямні косинуси:
має напрямні косинуси: 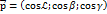 то рівняння площини має вигляд6 xcos𝓛 +ycosβ +zcosγ -p=0. 5. Нормальне рівняння площини:
то рівняння площини має вигляд6 xcos𝓛 +ycosβ +zcosγ -p=0. 5. Нормальне рівняння площини: 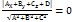 . Маючи нормальне рівняння знах відстань від довільної точки М0 (х0; y0; z0) до площини
. Маючи нормальне рівняння знах відстань від довільної точки М0 (х0; y0; z0) до площини 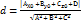 .
.
Т3. З6. Складання рівняння у просторі. 1. Загальне рівняння прямої у просторі. Оскільки кожна пряма є лінією перетину двох площин то рівняння цієї прямої є по суті системою двох рівнянь: 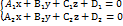 . 2. Рівняння прямої за точкою і напрямним вектором. М0 (х0; ху; z0),
. 2. Рівняння прямої за точкою і напрямним вектором. М0 (х0; ху; z0), 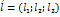 ,
, 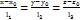 . 3. Параметричне рівняння прямої.
. 3. Параметричне рівняння прямої. 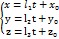 ,
, 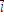 - напрямний вектор, (х0; ху; z0)- точка на прямій, t- параметр. 4. Рівняння прямої за двома точками (канонічне рівняння прямої). М1 (х1; y1; z1), М2 (х2; y2; z2),
- напрямний вектор, (х0; ху; z0)- точка на прямій, t- параметр. 4. Рівняння прямої за двома точками (канонічне рівняння прямої). М1 (х1; y1; z1), М2 (х2; y2; z2), 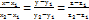 .
.
Т3. З7. Лінії другого порядку. Лініями другого порядку наз плоскі, криві які задаються рівнянням: Ах2+Вхy+Сy2+Dx+Ey+F=0. Два конуса зі спільною вершиною і віссю утвор фігуру яка наз математичним конусом. Всі лінії другого порядку є перерізами математичного конуса площинами: 1. Коло. Площина перпендикулярна до осі конуса. Коефіцієнт В=0, А=С. канонічне рівняння кола: (х-х0)2+(у-у0)2=R. Колом наз множини точок на площині рівновіддалених від заданої точки яка наз його центром. 2. Еліпс. Площине не перпендикулярна до осі і перетинає одну частину математичного конуса. У аг рівняння коефіцієнт А і С мають один знак але не рівні. Канонічне рівняння еліпса: 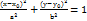 . a і b- велика і мала півосі. Велика та мала півосі можуть мінятися місцями. Еліпсом наз множина точок на площині сума відстаней від яких до двох заданих точок F1 та F2 є величина постійна. Точка F1 та F2 наз фокусами еліпса. Відстань F1 та F2 – фокальна відстань еліпса. F1 F2=2С – фокальна відстань. Якщо а – велика піввісь еліпса, то число ε =
. a і b- велика і мала півосі. Велика та мала півосі можуть мінятися місцями. Еліпсом наз множина точок на площині сума відстаней від яких до двох заданих точок F1 та F2 є величина постійна. Точка F1 та F2 наз фокусами еліпса. Відстань F1 та F2 – фокальна відстань еліпса. F1 F2=2С – фокальна відстань. Якщо а – велика піввісь еліпса, то число ε =  наз ексцентриситет. Чим ближче ексцентриситет до 0, тим еліпс ближчий до кола і навпаки. Фокальна відстань еліпса заданого канонічного рівняння знах за формулою: с=
наз ексцентриситет. Чим ближче ексцентриситет до 0, тим еліпс ближчий до кола і навпаки. Фокальна відстань еліпса заданого канонічного рівняння знах за формулою: с= 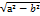 . Прямі х=
. Прямі х=  та х=
та х= 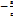 або що те ж саме х=
або що те ж саме х=  наз директрисами еліпсами. Властивість директрис: відношення фокального радіуса R2 до вільної точки еліпса до відстані від цієї точки до директриси є величина постійною.
наз директрисами еліпсами. Властивість директрис: відношення фокального радіуса R2 до вільної точки еліпса до відстані від цієї точки до директриси є величина постійною.
Т3. З9. Рівняння еліпса, гіперболи. Гіперболою наз множина точок на площині різниця відстаней від яких до двох заданих точок F1 та F2 є величиною постійною. F1 та F2 – наз фокусами гіперболи. F1 F2=2С – фокусна відстань гіперболи. Гіпербола утвор при перетині математичного конуса площиною паралельною до його осі. Канонічне рівняння гіперболи: 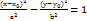 . a і b- півосі гіперболи. число ε =
. a і b- півосі гіперболи. число ε =  – ексцентриситет гіперболи. Фокусна відстань і півосі пов’язані рівністю с= а2+b2. Вісь ОХ наз дійсною віссю гіперболи, ОУ- уявною. Для того щоб побудувати гіперболу потрібно побудувати її основний прямокутник відступивши від центра вліво і вправо на піввісь а, вгору і вниз на піввісь b. Діагоналі цього прямокутника тобто прямі:
– ексцентриситет гіперболи. Фокусна відстань і півосі пов’язані рівністю с= а2+b2. Вісь ОХ наз дійсною віссю гіперболи, ОУ- уявною. Для того щоб побудувати гіперболу потрібно побудувати її основний прямокутник відступивши від центра вліво і вправо на піввісь а, вгору і вниз на піввісь b. Діагоналі цього прямокутника тобто прямі: 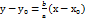 є асимптотами гіперболи (прямими до яких графік наближається на нескінченості, але не перетинає). Якщо вісь ОХ дійсна вісь гіперболи то вершини гіперболи лежать на серединах бічних сторін основного прямокутника. Якщо рівняння гіперболи має вигляд
є асимптотами гіперболи (прямими до яких графік наближається на нескінченості, але не перетинає). Якщо вісь ОХ дійсна вісь гіперболи то вершини гіперболи лежать на серединах бічних сторін основного прямокутника. Якщо рівняння гіперболи має вигляд 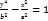 .
.
Т3. З10. Рівняння параболи. Парабола утвор при перетині математичного конуса площиною паралельною до його твірної. Параболою наз множина точок на площині рівновіддалених від заданої прямої (директриси) і заданої точки (фокуса). Канонічне рівняння параболи: (у-у0)2=2р(х-х0).
Т4. З1. Границя функції. Нехай задано неперервну функцію у= f(х). всі значення змінної х, які задовольняють нерівність 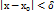 утворюють на осі ОХ δ - окіл точки ХО. Числа А наз границею функції у= f(х) в точці
утворюють на осі ОХ δ - окіл точки ХО. Числа А наз границею функції у= f(х) в точці 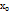 якщо для будь-якого як завгодно малого додатного ε знайдеться таке додатне залежне від ε число δ (ε ) що з нерівності 0<
якщо для будь-якого як завгодно малого додатного ε знайдеться таке додатне залежне від ε число δ (ε ) що з нерівності 0<  випливає нерівність
випливає нерівність 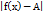 < ε,
< ε, 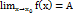 . A=
. A= 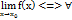 ε >
ε >  δ (ε )=0: 0<
δ (ε )=0: 0< 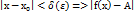 < ε. Очевидно що якщо функція f(х) в точці
< ε. Очевидно що якщо функція f(х) в точці 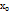 неперервна то границя цієї функції при
неперервна то границя цієї функції при 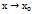 = значенню функції в цій точці. Функція у= f(х) наз неперервною в точці
= значенню функції в цій точці. Функція у= f(х) наз неперервною в точці 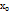 якщо для будь-якого як завгодно малого додатного ε околу точки А знайдеться таке додатне залежно від ε число δ що з нерівності 0<
якщо для будь-якого як завгодно малого додатного ε околу точки А знайдеться таке додатне залежно від ε число δ що з нерівності 0<  слідує нерівність
слідує нерівність 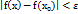 . По-іншому якщо А функції в точці
. По-іншому якщо А функції в точці 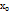 = значенню функції в цій точці то у= f(х) в точці
= значенню функції в цій точці то у= f(х) в точці 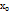 неперервна.
неперервна. 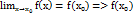 - неперервна точці
- неперервна точці 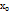 .
.
Похідна і диференціал функції. Нехай задано неперервну в точці х функцію у= f(х). Надамо в точці ∆ х деякого приросту і отримаємо нову точку x+∆ x. Пряма яка перетинає графік функції в двох точках a I b наз січною. Для того щоб знайти кут … розглянемо ∆ ABC. Маємо АС =∆ х ВС =∆ y, де ∆ y=f(x+∆ х 0-f(x) - приріст функції. Отже tg𝓛 = 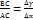 . Прифіксованій точці А будемо зменшувати
. Прифіксованій точці А будемо зменшувати 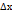 до 0. При цьому точка В по графіку наближається до точки А. якщо для кожного
до 0. При цьому точка В по графіку наближається до точки А. якщо для кожного 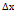 проводити прямі то отримаємо нескінчену кількість січних які проходять через А. граничним положенням січної при умові
проводити прямі то отримаємо нескінчену кількість січних які проходять через А. граничним положенням січної при умові 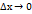 є дотична проведена до графіка функції y=f(x) в точці х. якщо 𝝋 - кут нахилу дотичної до додатного напрямку осі ОХ то з рівності tg=
є дотична проведена до графіка функції y=f(x) в точці х. якщо 𝝋 - кут нахилу дотичної до додатного напрямку осі ОХ то з рівності tg= 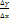 слідує tg𝝋 =
слідує tg𝝋 = 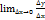 . Похідною функції y=f(x) наз границя відношення приросту функції до приросту аргумента при умові що приріст аргумента прямує до 0 f’(x)=
. Похідною функції y=f(x) наз границя відношення приросту функції до приросту аргумента при умові що приріст аргумента прямує до 0 f’(x)= 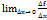 .. В багатьох задачах математичного аналізу приріст функції обчислити доволі складно у таких випадках його приблизно замінюють на приріст дотичної який наз диференціалом функції y=f(x) і познач dy по df. З ∆ ABC маємо: АС =∆ X, tg𝝋 =
.. В багатьох задачах математичного аналізу приріст функції обчислити доволі складно у таких випадках його приблизно замінюють на приріст дотичної який наз диференціалом функції y=f(x) і познач dy по df. З ∆ ABC маємо: АС =∆ X, tg𝝋 = 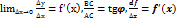 . Отже, df(x)=f’(x)*df. Число А наз границею функції f(x) в точці x0 якщо для будь-якого ε околі точки А знайдеться такий δ окіл точки x0 який функцією f(x) перетинається ε в окіл точки А.
. Отже, df(x)=f’(x)*df. Число А наз границею функції f(x) в точці x0 якщо для будь-якого ε околі точки А знайдеться такий δ окіл точки x0 який функцією f(x) перетинається ε в окіл точки А.
Т4. З3. Обчислення границі функції. Основні типи невизначеності: 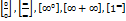 . При знаходжені границь потрібно вміти розкривати невизначеність. Кожен тип невизначеності розкривається своїми методами. При цьому часто використовують чудові границі: 1.
. При знаходжені границь потрібно вміти розкривати невизначеність. Кожен тип невизначеності розкривається своїми методами. При цьому часто використовують чудові границі: 1. 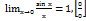 . 2.
. 2. 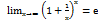 ,
, 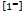 . 3.
. 3. 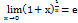 4.
4. 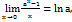
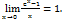 При розкриті невизначеності
При розкриті невизначеності 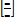 яка утворилась внаслідок ділення многочленів потрібно чисельник і знаменник поділити на найбільший степінь невідомої.
яка утворилась внаслідок ділення многочленів потрібно чисельник і знаменник поділити на найбільший степінь невідомої.
Т4. З4. Неперервність функції. Оскільки вісь Ох є неперервною множиною точок то до точки x0 на цій осі можна наближатися як зліва так і справа. Відповідно можна ввести поняття лівосторонньої границі функції f(x) в точці x0 та правосторонньої 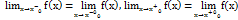 . Очевидно що необхідною умовою існування границі функції в точці є існування і рівність лівосторонньої та правосторонньої границі. Отже число А є границею функції
. Очевидно що необхідною умовою існування границі функції в точці є існування і рівність лівосторонньої та правосторонньої границі. Отже число А є границею функції 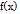 в точці якщо існують і рівні між собою односторонні границі цієї функції які = числу А
в точці якщо існують і рівні між собою односторонні границі цієї функції які = числу А 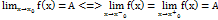 . . таким чином функція
. . таким чином функція 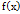 наз неперервною в точці x0 якщо в цій точці існують і рівні між собою лівостороння і правостороння границі які = значенню функції в точці x0
наз неперервною в точці x0 якщо в цій точці існують і рівні між собою лівостороння і правостороння границі які = значенню функції в точці x0 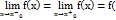 x0). Класифікація точок розриву функції. Якщо не виконується хоча б одна умова в означені неперервності то точка наз точкою розриву функції а функція наз розривною в цій точці. 1. Нехай
x0). Класифікація точок розриву функції. Якщо не виконується хоча б одна умова в означені неперервності то точка наз точкою розриву функції а функція наз розривною в цій точці. 1. Нехай 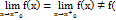 x0)2. Нехай
x0)2. Нехай  3. Нехай хоча б одностороння границя =∞
3. Нехай хоча б одностороння границя =∞ 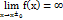 . Перші два випадки наз точками усувного розриву асимптота неусувний розриі. Асимптоти функції. 1. Вертикальні асимптоти(в. а. ). Для знах в. а. потрібно знайти всі точки розриву функції і обчислити границю функції в них. Якщо границя f(x) в точці x0 =∞ то x=x0 – рівняння в. а. 2. Похилі асимптоти(п. а. ) y=kx+b,
. Перші два випадки наз точками усувного розриву асимптота неусувний розриі. Асимптоти функції. 1. Вертикальні асимптоти(в. а. ). Для знах в. а. потрібно знайти всі точки розриву функції і обчислити границю функції в них. Якщо границя f(x) в точці x0 =∞ то x=x0 – рівняння в. а. 2. Похилі асимптоти(п. а. ) y=kx+b, 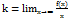 ,
, 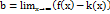 .. якщо k=0 і b≠ ∞ то отримуємо горизонтальну асимптоту.
.. якщо k=0 і b≠ ∞ то отримуємо горизонтальну асимптоту.
Т4. З5. Дослідження функції на неперервність. Теорема: якщо в точці x0 є неперервними функції f(x) I g(x) то в цій точці будуть неперервними наступні функції: 1. 𝓛 f(x)+β g(x) 2. F(x)*g(x) 3. 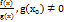 . Теорема (неперервність складеної функції): якщо функція f(u) неперервна в точці u0 а функція 𝝋 (x) неперервна в точці x0 при чому 𝝋 (x0)= u0 то в точці x0неперервною є складена функція F(x)=f(𝝋 (x)). Теорема Вейєрштраса: нехай функція y=f(x) неперервна в кожній точці деякого проміжку
. Теорема (неперервність складеної функції): якщо функція f(u) неперервна в точці u0 а функція 𝝋 (x) неперервна в точці x0 при чому 𝝋 (x0)= u0 то в точці x0неперервною є складена функція F(x)=f(𝝋 (x)). Теорема Вейєрштраса: нехай функція y=f(x) неперервна в кожній точці деякого проміжку 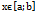 . Тоді: 1. На цьому проміжку існують точки в яких f(x) досягає свого найбільшого і найменшого значення. 2. Якщо С- деяке число з проміжку
. Тоді: 1. На цьому проміжку існують точки в яких f(x) досягає свого найбільшого і найменшого значення. 2. Якщо С- деяке число з проміжку 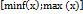 то знайдеться хоча б одне число
то знайдеться хоча б одне число 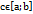 значення функції в якому = С, тобто f(c)=C. Теорема Больцано – Коші: якщо функція y=f(x) неперервна на проміжку
значення функції в якому = С, тобто f(c)=C. Теорема Больцано – Коші: якщо функція y=f(x) неперервна на проміжку 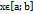 і на кінцях цього проміжку приймається значення різних знаків то на проміжку
і на кінцях цього проміжку приймається значення різних знаків то на проміжку 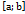 функція f(x)має при наймі один 0.
функція f(x)має при наймі один 0.
Т4. З6. Дослідження функції на асимптоти. Пряма наз асимптотою кривої якщо відстань від змінної точки кривої до цієї прямої при віддалені точки до нескінченості прямує до 0. Графік функції ніколи не може перетинати вертикальну асимптоту оскільки x=x0 не входить в ОДЗ функцій. Натомість похилу асимптоту графік може перетинати в нескінченій кількості точок 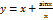 . Має похилу асимптоту y=x (k=1; b=0). 1. В. а.:
. Має похилу асимптоту y=x (k=1; b=0). 1. В. а.: 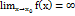 2. П. а.: y=kx+b,
2. П. а.: y=kx+b, 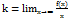 ,
, 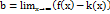 .
.
Т4. З7. Похідна функції. Означення похідної її геометричний та фізичний зміст. Геометричний зміст похідної (ГПЗ). Похідна функції y=f(x) знайдена в точці x0=tg кута нахилу дотичної проведеної до графіка функції f(x) в точці x0 до додатного напрямку осі ОХ f’(x)=tg𝝋. Фізичний зміст похідної (ФЗП). Нехай матеріальна точка рухається за законом S=S(t). тоді миттєва швидкість матеріальної точки в момент часу t = похідній від функції шляху V(t)=S’(t). Основні формули диференціювання. Операція знаходження похідної функції f(x) наз диференціюванням. Для того щоб знайти похідну функції довільної функції потрібно: 1. Знати табличку похідних елементарних функцій. 2. Знати і вміти використовувати правила знаходження похідних. Правила диференціювання: 1. (f(x)+g(x0)’=f’(x)+g’(x) 2. (cf(x)=Cf’(x)) 3. Похідна добутку (f(x)*g(x))’=f’(x)*g(x)+g’(x)*f(x). 4. Похідна частки 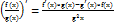 . 5. Похідна складеної функції. Нехай задано дві неперервні функції y=f(x)та g(x). якщо обчислити значення функції g в точці x і отримане число підставити замість аргумента в функцію f то утвориться нова функція y=f(g(x)) яка наз складеною. При цьому функція f наз зовн а g - вн.
. 5. Похідна складеної функції. Нехай задано дві неперервні функції y=f(x)та g(x). якщо обчислити значення функції g в точці x і отримане число підставити замість аргумента в функцію f то утвориться нова функція y=f(g(x)) яка наз складеною. При цьому функція f наз зовн а g - вн.
Т4. З9. Диференціал функції. Для приблизного знах функції при заданому прирості аргумента його заміняють на приріст дотичної проведеної до графіка функції в точці. З АВС маємо: ВС=АС tg y. Викор ГЗП і те що приріст незалежної змінної х є її диференціалом (∆ x=dx) отримуємо: dy=f’(x)dx - формула знах першого диференціала. Звідси слідує 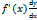 тобто похідна функції = відношенню її диференціала до диференціала аргументa. Вираз
тобто похідна функції = відношенню її диференціала до диференціала аргументa. Вираз 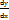 таким чином виступає окремим познач похідної (dy по dx). Похідні вищих порядків. Другою похідною функції наз похідна від її першої похідної f’’(x)=(f’(x))’. Похідною n–го порядку функції наз похідно від похідної (n-1)-го порядку цієї функції: f(n)(x)=(f(n-1)(x))’. Четверта похідна познач: f(4)(x). Фізичний зміст другої похідної. Оскільки перща похідна є миттєвою швидкістю зміни то друга похідна є швидкістю зміни швидкості тобто прискорення матеріальної точки в момент часу t0. Диференціали вищих порядків. Другим диференціалом функції наз диференціал від її першого диференціала. Оскільки dy=f’(x) то з формули слідує d(dy)=(dy)’*dx=(f’(x)*dx)’*dx=f’(x)’dx*dx. Отже другий диференціал функції знах за формулою: d2y=f’’(x)dx2. Звідси слідує
таким чином виступає окремим познач похідної (dy по dx). Похідні вищих порядків. Другою похідною функції наз похідна від її першої похідної f’’(x)=(f’(x))’. Похідною n–го порядку функції наз похідно від похідної (n-1)-го порядку цієї функції: f(n)(x)=(f(n-1)(x))’. Четверта похідна познач: f(4)(x). Фізичний зміст другої похідної. Оскільки перща похідна є миттєвою швидкістю зміни то друга похідна є швидкістю зміни швидкості тобто прискорення матеріальної точки в момент часу t0. Диференціали вищих порядків. Другим диференціалом функції наз диференціал від її першого диференціала. Оскільки dy=f’(x) то з формули слідує d(dy)=(dy)’*dx=(f’(x)*dx)’*dx=f’(x)’dx*dx. Отже другий диференціал функції знах за формулою: d2y=f’’(x)dx2. Звідси слідує 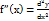 (де два у по де х квадрат).
(де два у по де х квадрат).
Т4. З10. Деякі теореми диференціального числення. Теорема про середнє. 1. Теорема Ролля. Нехай функція y=f(x): 1. Неперервна на відрізку 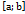 . 2. Диференційована на цьому відрізку. 3. На кінцях відрізках приймає однакові значення f(a)=f(b). Тоді існує така точка
. 2. Диференційована на цьому відрізку. 3. На кінцях відрізках приймає однакові значення f(a)=f(b). Тоді існує така точка 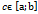 що f’(c)=0. 2. Теорема Лаграллса. Нехай функція y=f(x): 1. Неперервна на відрізку
що f’(c)=0. 2. Теорема Лаграллса. Нехай функція y=f(x): 1. Неперервна на відрізку 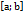 . 2. Диференційована на цьому відрізку. Тоді існує точка
. 2. Диференційована на цьому відрізку. Тоді існує точка 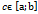 в якій
в якій 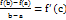 . 3. Теорема Коші. Нехай функції f(x) I 𝝋 (x) неперервні і диференційовані на проміжку
. 3. Теорема Коші. Нехай функції f(x) I 𝝋 (x) неперервні і диференційовані на проміжку 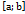 і в середині цього проміжку 𝝋 ’(x)
і в середині цього проміжку 𝝋 ’(x) 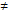 0. Тоді існує така точка
0. Тоді існує така точка 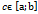 в якій
в якій 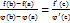 . Правило Лопіталя. Теорема 1: нехай функції f(x) I 𝝋 (x) неперервні диференційовані на відрізку
. Правило Лопіталя. Теорема 1: нехай функції f(x) I 𝝋 (x) неперервні диференційовані на відрізку 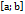 і в точці
і в точці 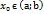 виконується нерівність:
виконується нерівність: 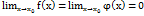 . Тоді
. Тоді 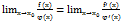 . Наслідок: якщо остання границя теж має невизначеність
. Наслідок: якщо остання границя теж має невизначеність 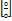 то диференціюємо чисельник і знаменник до тих пір дики не розкриємо невизначеність. Теорема 2: нехай функції f(x) I 𝝋 (x) неперервні і диференційовані на проміжку
то диференціюємо чисельник і знаменник до тих пір дики не розкриємо невизначеність. Теорема 2: нехай функції f(x) I 𝝋 (x) неперервні і диференційовані на проміжку 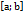 окрім точки
окрім точки 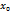 в якій виконується рівності:
в якій виконується рівності: 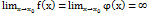 . Тоді
. Тоді 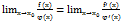 . Зауваження: теорема 1 та теорема 2(правило лопіталля) справджуються для невизначеностей типу
. Зауваження: теорема 1 та теорема 2(правило лопіталля) справджуються для невизначеностей типу 
 навіть у випадку коли x
навіть у випадку коли x  0.
0.
Т4. З10. Монотонність на екстремуми. Якщо на деякому проміжку 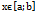 для функції y=f(x) з нерівності x1< x2 слідує нерівність f(x1)< f(x2) монотонно-зростаюча на цьому проміжку. Якщо з нерівності x1< x2=> f(x1)> f(x2) то монотонно-спадною. Дослідити функцію на монотонність означає знайти всі проміжки зростання і спадання цієї функції. Якщо в деякому околі точки для неперервної функції y=f(x) виконується нерівність f(x)< f(x0) то x0 наз точкою локального максимуму функції f(x). Якщо f(x)> f(x0) – то локального мінімуму. Точки логального мінімуму та максимуму наз точками екстремуму функції. Значення функції f(x) в цих точках наз екстремумами. Необхідна умова екстремуму функції (тоска Коші). Якщо в точці x0 неперервна і диференційована функція y=f(x) має екстремум то її похідна в цій точці = 0. Достатня умова екстремуму: нехай в точці x0 f’(x) =0. Якщо при переході через цю точку похідна f’(x) =0 змінює знак з + на – то – точка локального максимуму. Якщо з – на + -то точка локального мінімуму. Якщо при переході через x0 похідна не змінює знак то x0 не є точкою екстремуму. Схема дослідження функції на монотонність та екстремуми(метод інтервалів для першої похідної). 1. Знах похідну функції і прирівнюємо її до 0. 2. Знайдені точки і точки в яких похідна не існує наносимо на числову пряму. 3. Розбиваємо пряму на інтервали на кожному них ставимо знак першої похідної(підставивши довільне число з цього інтервалу замість х в похідну). 4. Проміжки зі знаком + є – зростання, з - - спадання. 5. Нулі похідної в яких відбувається змінна знаку є точкою відповідного екстремуму.
для функції y=f(x) з нерівності x1< x2 слідує нерівність f(x1)< f(x2) монотонно-зростаюча на цьому проміжку. Якщо з нерівності x1< x2=> f(x1)> f(x2) то монотонно-спадною. Дослідити функцію на монотонність означає знайти всі проміжки зростання і спадання цієї функції. Якщо в деякому околі точки для неперервної функції y=f(x) виконується нерівність f(x)< f(x0) то x0 наз точкою локального максимуму функції f(x). Якщо f(x)> f(x0) – то локального мінімуму. Точки логального мінімуму та максимуму наз точками екстремуму функції. Значення функції f(x) в цих точках наз екстремумами. Необхідна умова екстремуму функції (тоска Коші). Якщо в точці x0 неперервна і диференційована функція y=f(x) має екстремум то її похідна в цій точці = 0. Достатня умова екстремуму: нехай в точці x0 f’(x) =0. Якщо при переході через цю точку похідна f’(x) =0 змінює знак з + на – то – точка локального максимуму. Якщо з – на + -то точка локального мінімуму. Якщо при переході через x0 похідна не змінює знак то x0 не є точкою екстремуму. Схема дослідження функції на монотонність та екстремуми(метод інтервалів для першої похідної). 1. Знах похідну функції і прирівнюємо її до 0. 2. Знайдені точки і точки в яких похідна не існує наносимо на числову пряму. 3. Розбиваємо пряму на інтервали на кожному них ставимо знак першої похідної(підставивши довільне число з цього інтервалу замість х в похідну). 4. Проміжки зі знаком + є – зростання, з - - спадання. 5. Нулі похідної в яких відбувається змінна знаку є точкою відповідного екстремуму.
Т4. З14. Опуклість функції. Нехай задано неперервну двічі диференційовану функцію y=f(x). Якщо на деякому проміжку 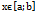 це функція має єдиний екстремум то вона наз опуклою вгору, якщо її графік розміщений вище відповідної хорди і опуклою вниз, якщо – нище. Точки в яких функція змінює тип опуклості наз точками перегину функції. Схема дослідження функції на опуклість(метод інтервалів для другої похідної). 1. Знаходимо другу похідну функції і прирівнюємо її до 0. 2. Знайдені розв’язки і точки в яких друга похідна не існує наносимо на числову пряму. 3. Розбиваємо пряму на інтервали і на кожному з них ставимо знак другої похідної. 4. На проміжках зі знаком + функція опукла вниз, - - вгору. Точки в яких відбулася зміна знаку другої похідної є точками перегину функції.
це функція має єдиний екстремум то вона наз опуклою вгору, якщо її графік розміщений вище відповідної хорди і опуклою вниз, якщо – нище. Точки в яких функція змінює тип опуклості наз точками перегину функції. Схема дослідження функції на опуклість(метод інтервалів для другої похідної). 1. Знаходимо другу похідну функції і прирівнюємо її до 0. 2. Знайдені розв’язки і точки в яких друга похідна не існує наносимо на числову пряму. 3. Розбиваємо пряму на інтервали і на кожному з них ставимо знак другої похідної. 4. На проміжках зі знаком + функція опукла вниз, - - вгору. Точки в яких відбулася зміна знаку другої похідної є точками перегину функції.
Т4. З16. Схема дослідження функції і побудова графіка. 1. ОДЗ. 2. Точки перегину з осями координат: з ОХ(0; у(0)), з ОХ: розв’язків рівняння f(x)=0. 3. Парність та непарність. f(-x)= f(x) – функція парна (графік симетричний відносно осі ОУ), f(-x)=- f(x) - функція непарна (графік симетричний відносно початку координат). 4. Періодичність. 5. Монотонність на екстремуми. 6. Опуклість і точки перегину. 7. Асимптоти а) вертикальні, б) похилі. 8. Побудова графіка.
Т5. З1. Елементи інтегрального числення. Функція F(x) наз первісною для функції f(x) на даному проміжку якщо виконується рівність F’(x)=f(x). Теорема: якщо функція F(x) є первісною для функції f(x) то будь-яка інша первісна для f(x) знах за формулою φ (x)=F(x)+c. Ця формула дає загальний вигляд первісної для функції f(x). Множинна всіх первісних для функції f(x) наз невизначеним інтегралом функції f(x) і познач 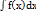 . Теорема: якщо F(x) - одна з первісних f(x) то має місце формула
. Теорема: якщо F(x) - одна з первісних f(x) то має місце формула 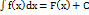 .
.
Т5. З2. Комплексні числа і дії над ними. Z=a+bi, a=reZ, b=ImZ, Z=r(cos𝝋 +isin𝝋 ), r= 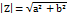 , 𝝋 =argz=arctg
, 𝝋 =argz=arctg  +π n, z=r*ei𝝋 . Дії над тригонометричною формулою комплексних чисел: нехай Z1=r1(cos𝝋 1+isin 𝝋 1), Z2=r2 (cos𝝋 2+isin 𝝋 2), Z1=Z2=r1r2(cos𝝋 1* cos𝝋 2+ isin 𝝋 1* isin 𝝋 2+ isin 𝝋 1 cos𝝋 2+ I2sin 𝝋 1* sin 𝝋 2)=r1r2(cos𝝋 1* cos𝝋 2-sin 𝝋 1* sin 𝝋 2+ i(sin 𝝋 1 cos𝝋 2+ cos 𝝋 1* sin 𝝋 2)). 1. Множення. Z1=Z2=r1r2 (cos(𝝋 1 +𝝋 2)+ isin (𝝋 1+𝝋 2)). 2. Ділення.
+π n, z=r*ei𝝋 . Дії над тригонометричною формулою комплексних чисел: нехай Z1=r1(cos𝝋 1+isin 𝝋 1), Z2=r2 (cos𝝋 2+isin 𝝋 2), Z1=Z2=r1r2(cos𝝋 1* cos𝝋 2+ isin 𝝋 1* isin 𝝋 2+ isin 𝝋 1 cos𝝋 2+ I2sin 𝝋 1* sin 𝝋 2)=r1r2(cos𝝋 1* cos𝝋 2-sin 𝝋 1* sin 𝝋 2+ i(sin 𝝋 1 cos𝝋 2+ cos 𝝋 1* sin 𝝋 2)). 1. Множення. Z1=Z2=r1r2 (cos(𝝋 1 +𝝋 2)+ isin (𝝋 1+𝝋 2)). 2. Ділення. 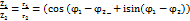 . 3. Формула Муавра. Z=r(cos𝝋 +isin 𝝋 ), Zn=rn(cos n𝝋 +isin n𝝋 ) 4. Корінь –го порядку Z=r(cos𝝋 +isin 𝝋 ),
. 3. Формула Муавра. Z=r(cos𝝋 +isin 𝝋 ), Zn=rn(cos n𝝋 +isin n𝝋 ) 4. Корінь –го порядку Z=r(cos𝝋 +isin 𝝋 ), 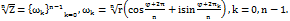 Розкладання раціональних функції на елементарний дроби. Нехай знаменник раціональної функції розкладений на множники двох видів: ax2+bx+c (D< 0), kx+m. Тоді ця функція є сумою елементарних дробів знаменника яких є далі множником а чисельники многочленами меншою на 1 степеня. Числа А, В, С, … знах методом невизначених коефіцієнтів. Теорема: два многочлена тотожно рівні тільки при умові рівноти їх коефіцієнтів при однакових степенях невідомої. 1. Помножаємо рівність на спільний знаменник. 2. Розкриваємо дужки і зводимо у правій частині подібні дроби. 3. Прирівнявши відповідні коефіцієнти лівої і правої частини отримуємо систему лінійних рівнянь з невідомими коефіцієнтами А, В, С, ….
Розкладання раціональних функції на елементарний дроби. Нехай знаменник раціональної функції розкладений на множники двох видів: ax2+bx+c (D< 0), kx+m. Тоді ця функція є сумою елементарних дробів знаменника яких є далі множником а чисельники многочленами меншою на 1 степеня. Числа А, В, С, … знах методом невизначених коефіцієнтів. Теорема: два многочлена тотожно рівні тільки при умові рівноти їх коефіцієнтів при однакових степенях невідомої. 1. Помножаємо рівність на спільний знаменник. 2. Розкриваємо дужки і зводимо у правій частині подібні дроби. 3. Прирівнявши відповідні коефіцієнти лівої і правої частини отримуємо систему лінійних рівнянь з невідомими коефіцієнтами А, В, С, ….
Т5. З4. Інтеграл функції. При безпосередньому інтегрувані потрібно знати таблицю інтегралів і правила інтегрування. Лінійні операції інтегрування. 1. 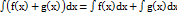 . 2.
. 2.  3. Якщо F(x) – первісна для f(x) то
3. Якщо F(x) – первісна для f(x) то 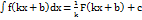 .
.
Т5. З10. Визначений інтеграл. Нехай на відрізку 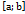 задано неперервну функцію y=f(x). Фігура задана на цьому відрізку і обмежена зверху графіком функції а знизу віссю ОХ наз криволінійною трапецією. Задача: розіб’ємо точне значення площі криволінійної трапеції. Розіб’ємо відрізок
задано неперервну функцію y=f(x). Фігура задана на цьому відрізку і обмежена зверху графіком функції а знизу віссю ОХ наз криволінійною трапецією. Задача: розіб’ємо точне значення площі криволінійної трапеції. Розіб’ємо відрізок 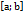 точками x0=a, x1,, x2, … xn =b на частини. Знайшовши значення функції в кожній з точок розбиття можемо утворити ждеяку східчасту фігуру утворену з прямокутників з шириною ∆ x і висотою F(x). Площа катого прямокутника = ∆ S=f(xk)∆ x. Тому площа східчастої фігури Sn знах як сума площ всіх прямокутників
точками x0=a, x1,, x2, … xn =b на частини. Знайшовши значення функції в кожній з точок розбиття можемо утворити ждеяку східчасту фігуру утворену з прямокутників з шириною ∆ x і висотою F(x). Площа катого прямокутника = ∆ S=f(xk)∆ x. Тому площа східчастої фігури Sn знах як сума площ всіх прямокутників 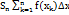 . Очевидно що Sn дає приблизне значення площі криволінійної трапеції. Для того щоб знайти точніше значення площі криволінійної трапеції потрібно збільшити кількість точок розбиття суми Sn наз інтегральними сумами функції f(x) на відрізку
. Очевидно що Sn дає приблизне значення площі криволінійної трапеції. Для того щоб знайти точніше значення площі криволінійної трапеції потрібно збільшити кількість точок розбиття суми Sn наз інтегральними сумами функції f(x) на відрізку 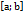 . Для знаходження точок значення площі криволінійної трапеції потрібно знайти границю при n→ ∞ таких інтегральних сум Skp. тр.
. Для знаходження точок значення площі криволінійної трапеції потрібно знайти границю при n→ ∞ таких інтегральних сум Skp. тр. 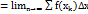 . Границя інтегральних сум функції f(x) на відрізку
. Границя інтегральних сум функції f(x) на відрізку 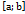 при умові n→ ∞ що наз визначеним інтегралом цієї функції на заданому відрізку і познач
при умові n→ ∞ що наз визначеним інтегралом цієї функції на заданому відрізку і познач 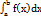 . Не дивлячись на суттєву відмінність означень визначеного і невизначеного інтегралів існує формула яка поєднує ці два поняття. Формула Ньютона – Лейбніца
. Не дивлячись на суттєву відмінність означень визначеного і невизначеного інтегралів існує формула яка поєднує ці два поняття. Формула Ньютона – Лейбніца 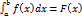 |ba=F(b)-F(a)/
|ba=F(b)-F(a)/
Т5. З7. Обчислення невизначеного інтеграла методом інтегрування частинами. Оскільки (u*v)’=u’*v+v’*u то (u*v)’dx=u’vdx+v’udx враховуючи те що df=f’dx маємо d(uv’)=vdu+udv. Про інтегрувавши останню рівність отримаємо 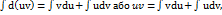 . Звідси виводиться основна формула методу інтегрування частинами:
. Звідси виводиться основна формула методу інтегрування частинами: 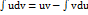 . За функцією вибирається та частина підінтегральної функції при якій вираз є простішим від виразу.
. За функцією вибирається та частина підінтегральної функції при якій вираз є простішим від виразу.
Т5. З11. Застосування визначеного інтеграла. 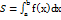 ,
, 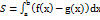 ,
, 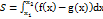 ,
, 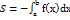 . Об’єм тіла обертання. Нехай графік невід’ємної функції y=f(x) на проміжку
. Об’єм тіла обертання. Нехай графік невід’ємної функції y=f(x) на проміжку 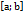 обертається навколо осі ОХ. Тіло обмежене утвореного поверхнею наз тілом обертанням. a) S=π f2(x), V=π
обертається навколо осі ОХ. Тіло обмежене утвореного поверхнею наз тілом обертанням. a) S=π f2(x), V=π 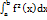 . f(x) наз твірною тіла обертання. б) V=π
. f(x) наз твірною тіла обертання. б) V=π 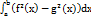 . Нехай тіла обертання з порожниною задається двома твірними: зовн y=f(x) і вн y=g(x). Маса однорідного стержня. Нехай густина ρ (x) розподілена вздовж стержня довжиною l нерівномірно m=
. Нехай тіла обертання з порожниною задається двома твірними: зовн y=f(x) і вн y=g(x). Маса однорідного стержня. Нехай густина ρ (x) розподілена вздовж стержня довжиною l нерівномірно m= 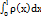 . Нехай матеріальна точка рухається прямолінійно нерівномірно з швидкістю V=V(t) тоді шлях пройдений цією точкою від моменту часу t1 до t2 знах за формулою: S=
. Нехай матеріальна точка рухається прямолінійно нерівномірно з швидкістю V=V(t) тоді шлях пройдений цією точкою від моменту часу t1 до t2 знах за формулою: S= 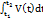 .
.
Т. 5 Зн. 18 Застосув. Визначеного інтегралу. Метод заміни змінної. Нехай підінтегральна функція має вигляд: f(g(x)) * g`(x) Тоді використ. формулу диференціала І-го порядку dg(x) = g`(x) dx Даний інтеграл можна звести до вигляду: ∫ f(g(x)) * g`(x) dx = ∫ f(g(x)) * dg(x) Зробити заміну g(x) = t Зводимо цей інтеграл до простішого вигляду ∫ f(t)dt У випадку визначеного інтеграла ця формула приймає вигляд: 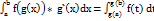
Т. 5 Зн. 20Інтегрування тригонометр. виразів. 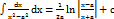 .
.
При інтегруванні тригоном. Виразів, особливо таких які містять дроби, часто не допомагають ні інтегрування частинами, ні методи заміни. У таких випадках можемо застосувати універсальну тригонометр. підстановку,
За допомогою якої будь-яку тригонометричну функцію можна перевести в дробово-раціональний вираз. УТП( універсальна тригонометр. підстанова) Нехай tg  =Z, тоді sinx =
=Z, тоді sinx = 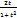 ; x = 2arctgt; cosx =
; x = 2arctgt; cosx = 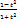 ; dx =
; dx = 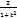 dt.
dt.
Т. 6 Зн. 1 Диференціальнірівняння І-го порядку. Рівняння, яке міститьневідомуфункцію, їїпохідні та аргумент назив. Диференціальнимирівняннями. F (x, y, y`, y``, …) = 0. Рівняння, яке містить невідому функцію разом з її першою похідною назив. Диференціальним рівнням першого порядку. F (x, y, y`) = 0. Найпростіше диф. рівняння 1-го порядку має виглядy` = f(x), де f(x)- задана функція. Загал. розв’язок рівняння має виглядy(x) = ∫ f(x) dxМножина всіх розв’язків диференціального рівняння утвор. його загал. розв’язок. Загальний розв’язок диф. рівняння 1-го порядку є множина функцій, які відрізняються між собою сталим доданком. Отже, графіки цих функцій зміщені один відносно іншого вздовж осі ОУ. Тому через кожну точку на площині проходить лише одна функція, яка назив. частинним розв’язком диференціального рівняння, що задовольняє умову:
y( 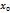 ) =
) = 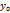 . Нехай диференціальне рівняння 1-го порядку має вигляд
. Нехай диференціальне рівняння 1-го порядку має вигляд
y`(x) = f(x; y), де f(x; y) =  . тоді дане диф. рівняння можна розв’язати, розділивши змінні dy = y`dx звідси y`=
. тоді дане диф. рівняння можна розв’язати, розділивши змінні dy = y`dx звідси y`= 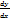
вираз читається dyпо dx i означає 1-шу похіднуфункціїyпо змінній х.
Тому, початкове рівняння можна звести до вигляду 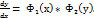
Дане рівняння назив. диф рівняння 1-го порядку з відокремлюваними змінними. 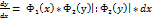 .
. 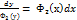
Проінтегрувавши обидві частини цієї рівності по відповідним змінним, отримаємзаг. розв’язокдиф. рівняння.
Т. 6 Зн. 2 Розв’язування дифер. рівнянь першого порядку з відокремлюваними змінними. Дифер. рівнянняM(x) dx + N(y) dy = 0 наз. Рівнянням з відокремленими змінними. Якщо розв’язок цього рівняння можна подати у явному вигляді, то він наз. Загальним розв’язком рівняння.
Якщо невідому функцію у(х) не можна явно виразити через х, то в такому випадку записують загальний інтеграл рівняння, тобто формулу яка містить аргумент х і невідому функцію. Загальний інтеграл рівняння з відокремленими змінними має вигляд ∫ M(x) dx + ∫ N(y) dy = C, c = const. Дифер. рівняння 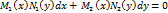 назив. рівняння з відокремлюваними змінними.
назив. рівняння з відокремлюваними змінними. 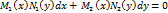 |
| 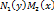 .
. 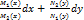 = 0 Загальнийінтеграл:
= 0 Загальнийінтеграл:  = С.
= С.
Т. 6 Зн. 3 Однорідні дифер. рівняння першого порядку.
Функція f(x; y) назив. однорідною функцією розмірності n якщо виконується рівність f (λ x, λ y) = 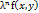 . f(x, y) =
. f(x, y) = 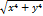 . f(λ x, λ y) =
. f(λ x, λ y) = 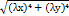 =
= 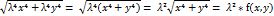 .
. 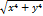 – одноріднафункція розмірності 2. f(x, y) =
– одноріднафункція розмірності 2. f(x, y) = 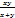 , f (λ x, λ y) =
, f (λ x, λ y) = 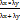 =
= 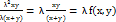 ,
, 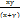 – однорыднафункцыя 1-го степеня, f (x, y) =
– однорыднафункцыя 1-го степеня, f (x, y) = 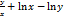 , f(λ x, λ y) =
, f(λ x, λ y) = 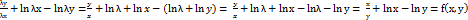 однорідна функція нульового степеня. Дифер. рівняння
однорідна функція нульового степеня. Дифер. рівняння 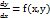 , де
, де 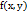 -однорідна функція нульового степеня, назив. однор. дифер. р-ння 1-го порядку. Оскількиf(λ x, λ y) = f (x, y), то підставивши λ =
-однорідна функція нульового степеня, назив. однор. дифер. р-ння 1-го порядку. Оскількиf(λ x, λ y) = f (x, y), то підставивши λ =  , отримаємо f (x, y) = f(
, отримаємо f (x, y) = f(  x,
x,  y) = f (1,
y) = f (1,  ), тому однорідна функція 0-го степеня залежить фактично тільки від частки
), тому однорідна функція 0-го степеня залежить фактично тільки від частки  .
.
Робимозаміну  = u => y = xu.
= u => y = xu. 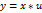 ,
, 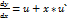 . Отже, u+xu` = f(x, x*u)
. Отже, u+xu` = f(x, x*u)
u+xu` = f(1, u). Вважаючиu функцією від x u=u(x), отрималидиф. рівняння з відокремлюваними змінними x* 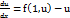 ,
, 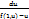 =
=  , заг. інтеграл якого ∫
, заг. інтеграл якого ∫ 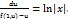 Повернувшись до заміни y =
Повернувшись до заміни y =  , отримаємзаг. інтеграл початкового, однорідного рівняння.
, отримаємзаг. інтеграл початкового, однорідного рівняння.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|