
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
О разных формах записи дифференциала
О разных формах записи дифференциала
Дифференциал функции в точке x и обозначают
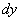
или

Следовательно,
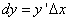 (1)
(1)
или
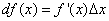 , (2)
, (2)
поскольку дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной.
Замечание. Нужно помнить, что если x – исходное значение аргумента, а 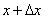 - наращенное значение, то производная в выражении дифференциала берётся в исходной точке x ; в формуле (1) этого не видно из записи.
- наращенное значение, то производная в выражении дифференциала берётся в исходной точке x ; в формуле (1) этого не видно из записи.
Дифференциал функции можно записать в другой форме:
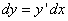 (3)
(3)
или
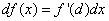 (4)
(4)
Свойства дифференциала
В этом и следующем параграфах каждую из функций будем считать дифференцируемой при всех рассматриваемых значениях её аргументов.
Дифференциал обладает свойствами, аналогичными свойствам производной:
 (С – постоянная величина) (5)
(С – постоянная величина) (5)
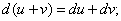 (6)
(6)
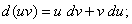 (7)
(7)
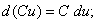 (8)
(8)
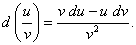 (9)
(9)
Формулы (5) – (9) получаются из соответствующих формул для производной умножением обеих частей каждого равенства на 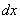 .
.
Одно из особеннейших свойств дифференциала - инвариантность формы дифференциала в случае сложных функций
Пример 1. Найти дифференциалы функций:
1) 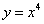 ;
;
2) 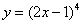 ;
;
3)  ;
;
4) 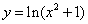 .
.
Решение. Применяя формулы дифференцироивания степенной и логарифмической функций из таблицы производных, а также формулу (4), находим:
1)  ;
;
2) 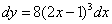 ;
;
3) 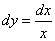 ;
;
4) 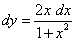 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|