Клеман-Дезорм әдісімен ауа үшін адиабат

Стр 1 из 4Следующая ⇒

Қ азақ стан республикасының білім жә не ғ ылым министрлігі

Қ. И. Сә тбаев атындағ ы Қ азақ ұ лттық техникалық зерттеу университеті

Ә л-Машани атындағ ы базалық білім беру институты

Жалпы физика кафедрасы

ЗЕРТХАНАЛЫҚ ЖҰ МЫС№8

Клеман-Дезорм ә дісімен ауа ү шін адиабат

кө рсеткішін анық тау

Зертханалық сабақ қ а арналғ ан ә дістемелік нұ сқ ау

Алматы 2021

КЛЕМАН –ДЕЗОРМ Ә ДІСІМЕН АУА Ү ШІН

АДИАБАТ КӨ РСЕТКІШІН АНЫҚ ТАУ

Жұ мыстың мақ саты: Клеман-Дезорм ә дісімен жылу сыйымдылық тарының қ атынасын анық тау кезінде газдағ ы жү ретін изопроцестерді зерттеу жә не ауа ү шін 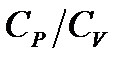қ атынасын анық тау.

Керекті қ ұ рал-жабдық тар: шыны баллон, су манометрі, компрессор, секундомер.

1. ТЕОРИЯЛЫҚ КІРІСПЕ

1кг заттың температурасын 1К-ге қ ыздыру ү шін қ ажетті жылу мө лшері меншікті жылу мө лшеріcдеп аталады:

Меншікті жылу сыйымдылық пен қ оса молярлық жылу сыйымдылық ты Сқ олданғ ан ың ғ айлы. 1моль заттың температурасын 1К-ге қ ыздыру ү шін қ ажетті жылу мө лшері молярлық жылу сыйымдылық Сдеп аталады:

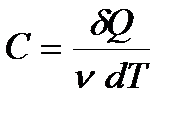, (1)

мұ ндағ ы 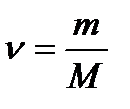– зат мө лшері, М– молярлық масса.

Меншікті с жә не молярлық жылу сыйымдылық тардың С арасындағ ы байланыс:

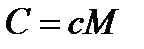орлардың ө лшем бірліктері 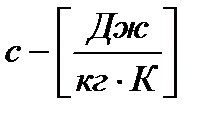жә не .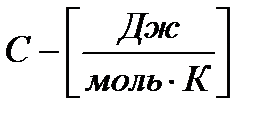

Егер заттың кө лемі V немесе қ ысымы Р тұ рақ ты болғ ан процесте тұ рақ ты кө лем кезіндегі ( жә не 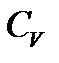) жә не тұ рақ ты қ ысым кезіндегі ( 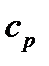жә не 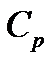) меншікті жә не молярлық жылу сыйымдылық тар болып ажыратылады.

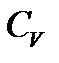жә не 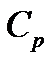-ларды термодинамиканың бірінші бастамасынан анық таймыз. Жү йеге берілген жылу мө лшері Q жү йенің (газдың ) ішкі энергиясын ө згертуге Δ U жә не газдың сыртқ ы кү штерге қ арсы атқ арғ ан жұ мысына А жұ мсалады:

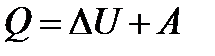
немесе дифференциалдық тү рде былай жазылады:

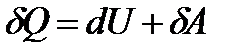. (2)

Жұ мыстың формуласын ескеріп:

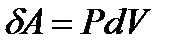(3)

жә не жылу мө лшерін 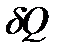(1) ө рнектен 1 моль газ ү шін термодинамиканың бірінші заң ын мына тү рде жазуғ а болады:

CdT=dU_M+pdV . (4)

Изохоралық процесс кезінде ( 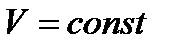) газдың атқ аратын жұ мысы нө лге тең (А=0). Ал сырттан газғ а берілген жылу, газдың ішкі энергиясын арттыруғ а (ө згертуге) жұ мсалады. Демек, массасы mгаздың температурасын арттырғ ан кезде оның ішкі энергиясы келесі шамағ а артады:

. (5)

Осыдан, массасы mгаздың температурасын арттырғ ан кезде, оның ішкі энергиясы келесі шамағ а артады:

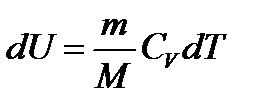. (6)

Егер газ изобаралық ( 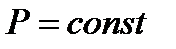) қ ызатын болса, онда (4) ө рнекті мына тү рде жазуғ а болады:

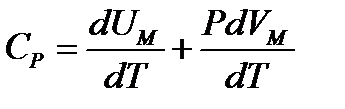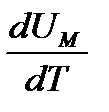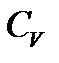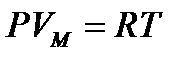мұ ндағ ы процесс тү ріне тә уелді болмайды (идеал газдың ішкі энергиясы қ ысымғ а да Р кө лемге де V тә уелді емес, тек температурамен анық талады) жә не ол ә рқ ашан -ғ а тең. Тұ рақ ты қ ысымда ( ) 1 мольгаз тең деуін дифференциалдасақ, онда универсал газ тұ рақ тысын аламыз, яғ ни:

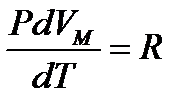Нә тижеде: 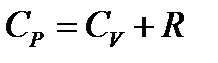. (7)

Бұ л ө рнек (7) Майер тең деуі деп аталады. C_Pә рқ ашан да 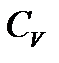-дан универсал газ тұ рақ тысынаR артық.

C_Pжә не 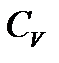жылу сыйымдылық тарын молекуланың дә режелер саны і арқ ылы ө рнектеуге болады (молекуланың кең істіктегі орнын толық анық тайтын тә уелсіз шамалар саны). Оны молекуланың «еркіндік дә режесі» деп те атайды.

1 моль идеал газдың ішкі энергиясы 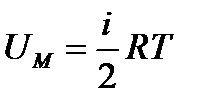болса, онда:

, .

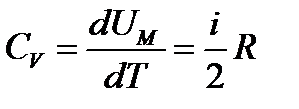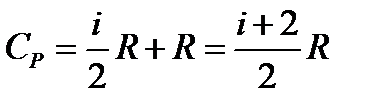Термодинамикалық процесстерді қ арастырғ ан кезде ә рбір газ ү шін 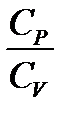қ атынасын 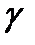арқ ылы белгілеу маң ызды сипатқ а ие:

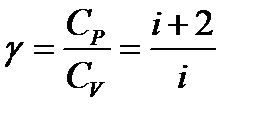. (8)

Молекулалардың еркіндік дә режесі ідеп, молекулалардың кең істікте орынын анық тайтын тә уелсізкоординаттар санын немесе молекулалардың кең істікте қ озғ ала алу мү мкіндіктер санын айтады: біратомды молекула ү шін і=3; екіатомды молекула ү шін і=5; ү шатомды жә не кө патомды молекулалар ү шін і=6.

Адиабаталық процесс тең деуіне кіретін 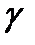шамасы адиабаттық кө рсеткіш деп аталады. Ол жү йе мен сыртқ ы орта арасында жылу алмасу болмайтындығ ымен ( 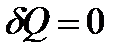) сипатталады. Бірінші жуық тауда тез жү ретін процестерді адиабаталық деп есептеуге болады.

Адиабаталық процесс ү шін термодинамиканың бірінші бастамасынан(2):

яғ ни сыртқ ы кү штердің жасайтын жұ мысы жү йенің ішкі энергиясының ө згеруі есебінен жү реді. Бұ л тең деуден (3) жә не (6) ө рнектерін ескере отырып, мына ө рнекті аламыз:

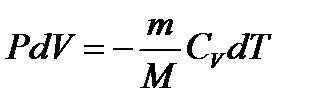. (9)

Бұ дан, газ кө лемінің ө згеруі оның температурасының ө згеруімен қ атар ө згеріп отырады. Минус таң басы адиабаталық ұ лғ аю кезінде (dV> 0) газдың салқ ындауын (dT< 0), ал адиабаталық сығ ылу кезінде (dV< 0) қ ызуын (dT> 0)кө рсетеді.

Идеал газ кү йінің негізгі тең деуін 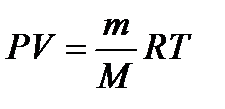дифференциалдап, мына тең деуді аламыз: .

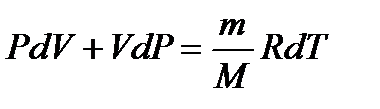Алынғ ан тең деуді (9) ө рнекке бө ліп жә не (7) жә не (8) ө рнектерді ескеріп келесі ө рнекті аламыз: .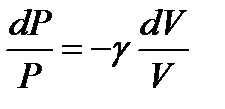

Бұ л тең деудің екі жағ ын P₁-ден P₂ дейін жә не V₁-ден V₂ дейін интегралдап тө мендегі тең деуге келеміз:

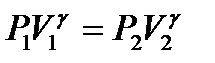. (10)

1 жә не 2 еркін таң дап алынғ ан кү йлер, сондық тан жалпы жағ дайдағ ы адиабаталық процесті мына тү рде жазуғ а болады:

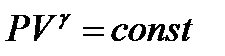. (11)

Бұ л тең деуді (11) Пуассон тең деуі деп атайды. Изотермиялық процесс тең деуі:

PV = const.

(11) тең деудегі адиабаталық кө рсеткішті 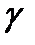Клеман-Дезорм ә дісімен тә жірибе жү зінде анық тауғ а болады.

12 3 4 Следующая ⇒