
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Примеры и разборы решения заданий тренировочного модуля
Примеры и разборы решения заданий тренировочного модуля
Пример 1. Найдем производную функции: 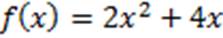
Решение: производная суммы равна сумме производных. Найдем производную каждого слагаемого
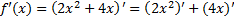

Ответ: 
Пример 2. Найти производную функции f(x)=8x3+3x2-x.
Решение:
f(x)=8x3+3x2-x
f’(x)=(8x3)’+(3x2)’-x’
Рассмотрим каждый член многочлена по отдельности
(8x3) '=8(x3) '=8·3x2=24x2
(3x2) '=3(x2) '=3·x=6x
(-x) '=-(x) = -1
f' (x)=(8x3) '+(3x2) '-x'=24x2+6x-1.
Ответ: f' (x)=24x2+6x-1.
Пример 3. Найти производную функции f(x)=(3x-4)(4-5x).
Решение: Воспользуемся формулой производной произведения:
f' (x)=(3х-4) ' (4-5х) + (3х-4)(4-5х) '=3(4-5х)-5(3х-4)=12-15х-15х+20= 32
Ответ: f' (x)=32
Пример 4. Найти производную функции 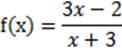
Решение: Воспользуемся формулой производной частного:
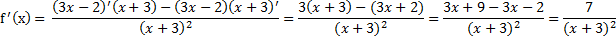
Ответ: 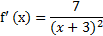
- Правила дифференцирования степенной функции.
Степенная функция – это функция вида y= xn.
Заметим, что в качестве степени 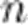 может быть как натуральное число, то есть 1, 2, 3, ...; так и любое отрицательное число: - 1, - 2 и т. д., а также и любое дробное, например, 2, 34; - 4, 1 или
может быть как натуральное число, то есть 1, 2, 3, ...; так и любое отрицательное число: - 1, - 2 и т. д., а также и любое дробное, например, 2, 34; - 4, 1 или  ,
, 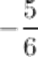 .
.
Степенной функцией с рациональным показателем называется функция вида: 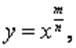 где x > 0, m, n - целые числа. Тогда степень
где x > 0, m, n - целые числа. Тогда степень 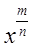 определяется равенством:
определяется равенством:
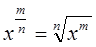 .
.
Например, 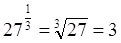 ;
; 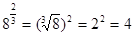 ;
; 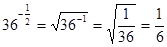
Перечислим основные свойства степени c рациональным показателем.
Пусть x и b – положительные действительные числа, а m, n, p, q – произвольные рациональные числа. Тогда справедливы следующие утверждения:
· 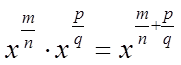
· 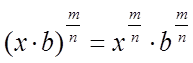
· 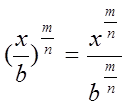
· 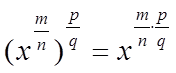
· 
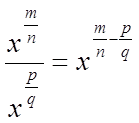
Производная степенной функции равна произведению показателя степени и основания в степени на единицу меньше.
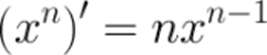
Примеры:
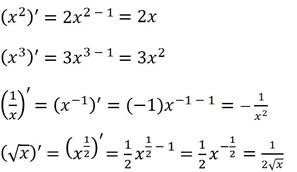
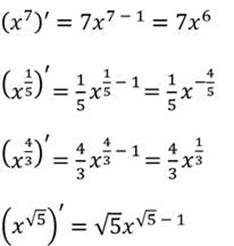
Примеры. Найдите производные функций:
а) 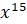 ; б)
; б) 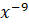 ; в)
; в) 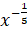 ; г)
; г) 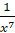 ; д)
; д) 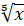 ; е)
; е) 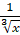 .
.
Решение.
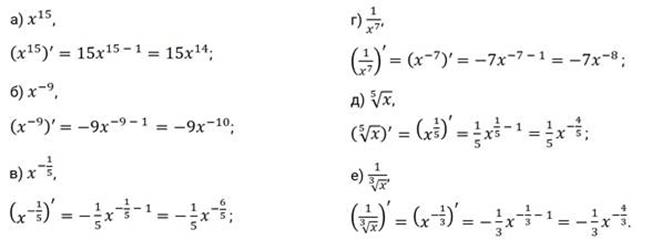
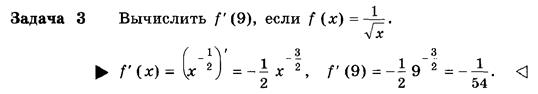






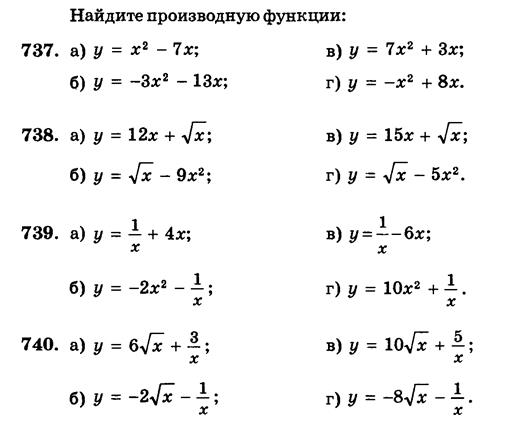

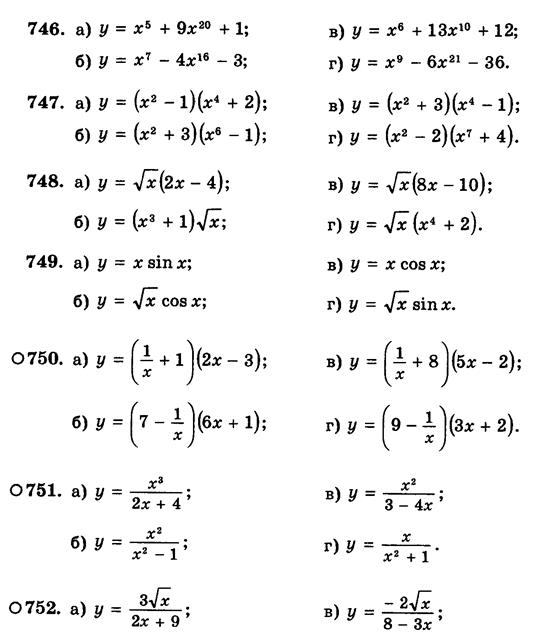

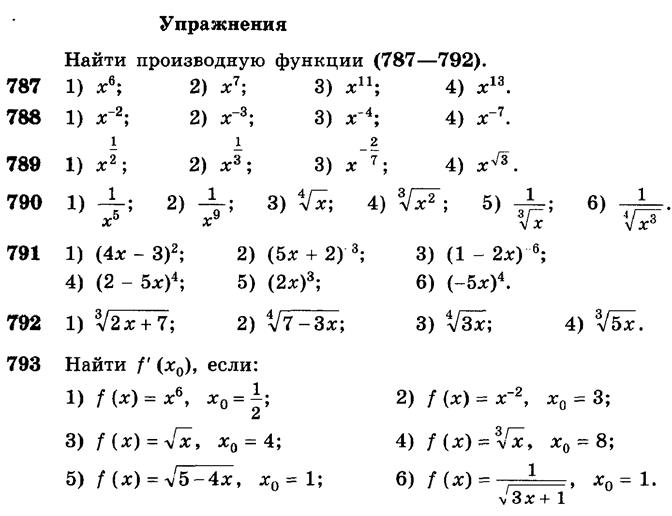




|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|