
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Контрольні запитання
1. Що таке відкриття? Об'єкти відкриття?
2. За якими ознаками технічне розв'язання задачі, визнається винаходом?
3. Що може бути об'єктом винаходу?
4. Які об'єкти інтелектуальної творчості не визнаються винаходами?
5. Що таке патент на винахід та який строк його дії?
6. Які документи входять до складу заявки на винахід?
7. Опис винаходу та його структура.
8. Формула винаходу, її значення і структура.
9. Куди подається заявка на винахід?
10. Що таке МПК (міжнародна патентна класифікація)?
11. Патентний пошук та його задачі.
12. Аналоги і прототип винаходу.
Лабораторна робота № 4
Статистична обробка осцилограм
Мета роботи: навчитись методам і порядку обробки осцилограм, отриманих при експериментальних дослідженнях випадкового процесу.
Теоретичні відомості
Більшість сільськогосподарських машин та агрегатів працюють в умовах, коли навантаження на їх робочі органи мають випадковий (непостійний і нерівномірний) характер. Наприклад, дія нерівностей поверхні поля на опорні колеса сільськогосподарських машин, нерівномірність щільності ґрунту за напрямком руху ґрунтообробної машини та маси врожаю, що подається на робочі органи зернозбирального комбайну і т. п.
Зміна дії випадкового процесу в часі чи просторі зветься реалізацією, а запис (фіксація результатів зміни) реалізації на реєструючому папері (моніторі, екрані і т. д. ) — осцилограмою. Якщо записувати один і той же процес декілька разів, то будемо мати ансамбль реалізацій випадкового процесу. На рисі подано ансамбль з трьох реалізацій випадкового процесу зміни нерівностей поверхні одного і того ж поля 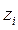 за декілька проходів І| по ньому сільськогосподарського об'єкта дослідження.
за декілька проходів І| по ньому сільськогосподарського об'єкта дослідження.

Рис. 1. Ансамбль реалізацій випадкового процесу
На перший погляд здається, що кожна з наведених ліній докорінно відрізняється від інших. Але водночас ми усвідомлюємо, що кожна з цих ліній характеризує нерівності одного і того ж поля. Тому за умов достатньої довжини реалізації кожна з них несе спільну загальну інформацію (реалізації мають спільний внутрішній стан) про випадковий процес.
Загальноприйнятими характеристиками випадкового процесу виступають математичне сподівання т, середнє квадратичне відхилення о та коефіцієнт варіації V. Для обчислення цих величин треба мати конкретні значення ординат випадкової величини, тобто експериментальний масив даних. Тому необхідно провести дискретизацію осцилограми безперервного випадкового процесу. Суть методики проведення дискретизації пояснюється на рис. 2
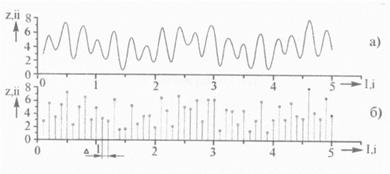
Рис. 2. Дискретизація реалізації випадкового процесу: а - безперервний тип; б - дискретний тип
Будь-який випадковий процес характеризується випадковими величинами, які завжди присутні в ході проведення експерименту.
Випадковою величиною називають величину, яка в результаті досліду може приймати різні величини. Випадкові величини, як правило, позначають великими літерами, наприклад X, а значення випадкової величини, яке вона приймає в результаті досліду, - малими літерами x1, x2, …., xN.
При великій кількості досліджень кожне із можливих значень випадкової величини x1, x2, …., xN може зустрітися b1, b2, …., bn разів. Ці числа називають частотами. Якщо всього було проведено N випробувань,
тобто 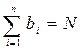 , то відношення
, то відношення 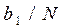 називають відносною частотою.
називають відносною частотою.
Сукупність, яка містить всі досліджувані величини, називається генеральною сукупністю.
Вибрані із генеральної сукупності N вимірів утворюють вибірку об'єму N.
Дискретними випадковими величинами називають такі величини, які можуть приймати лише визначені фіксовані значення, наприклад, 0, 1; 0, 2 і т. д.
Безперервними випадковими величинами називають такі величини, які в деякому інтервалі можуть приймати будь-які значення.
Наприклад, кількість бракованих деталей у різних вибірках із генеральної сукупності є дискретною випадковою величиною, а розмір цих деталей - безперервною випадковою величиною.
Всяку безперервну випадкову величину можна задати у вигляді дискретної, якщо всі можливі її значення розбити на інтервали і задати вірогідність появи цих інтервалів (визначення ординат випадкового процесу).
Кількість відрізків 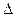 вздовж осі абсцис (тобто величина
вздовж осі абсцис (тобто величина 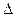 ) визначається, виходячи з максимальної частоти перебігу випадкового процесу (при виконанні роботи користуватися рекомендаціями розділу " Порядок виконання роботи", пункт 2).
) визначається, виходячи з максимальної частоти перебігу випадкового процесу (при виконанні роботи користуватися рекомендаціями розділу " Порядок виконання роботи", пункт 2).
Після проведення дискретизації і вимірювання ординат випадкового процесу отримаємо масив експериментальних даних. Якщо ці дані розподілити на класи, то можна побудувати графічне зображення експериментальних розподілів, для чого будуються гістограми і полігони розподілу частот з'явлення тієї чи іншої величини випадкового процесу.
Для графічного відображення експериментального масиву даних будуються гістограми і полігони розподілу.
Для випадкових величин дискретного типу застосовуються, як правило, полігони розподілу, а для випадкових величин безперервного типу - гістограми.
Розподіл випадкового процесу на класи можна виконати за правилом Штюргеса. Кількість класів випадкового процесу визначають за формулою:
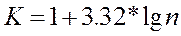 (1)
(1)
де 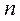 - кількість вибраних ординат в експериментальному масиві даних випадкового процесу.
- кількість вибраних ординат в експериментальному масиві даних випадкового процесу.
Результат обчислень за формулою (1) округлюють до цілого числа.
Інтервал кожного класу визначають за наступною формулою:
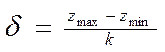 (2)
(2)
де 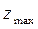 та
та 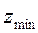 - відповідно максимальне та мінімальне чисельне значення виміряної ординати одного класу з експериментального масиву даних.
- відповідно максимальне та мінімальне чисельне значення виміряної ординати одного класу з експериментального масиву даних.
Полігони розподілів і гістограми будують за частотами розподілу експериментальних даних випадкового процесу.
Методика підрахування частот пояснюється табл. 1.
1. Розбивка масиву експериментальних даних на класи та методика обчислення частот розподілу
| Клас і*
| Межі інтервали класів
| Середини інтервалів zi,
| Частота | ||
| абсолютна Bi | відносна bi | Накопичена biн | |||
від zmax до zmin+ 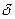 викл** викл**
| |||||
від zmin до zmln+ 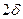 викл викл
| |||||
| …. | |||||
| k | від zmin+(k- 1) 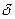 до zmax вкл*** до zmax вкл***
| ||||
Примітка: * i = 1, 2,.... к; **викл - виключно; ***вкл — включно.
Середини інтервалів кожного визначеного класу обчислюють за формулою:
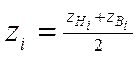 (3)
(3)
де 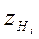 та
та 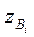 - відповідно нижня та верхня межа і-го класу.
- відповідно нижня та верхня межа і-го класу.
Абсолютна частота Вi - це кількість ординат (вимірів) з масиву даних, що потрапили до меж і-го класу.
Відносна частота bi ( визначається за формулою: 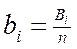 (4)
(4)
Накопичена частота і-го класу biН складається з суми відносних частот і-го та всіх попередніх класів.
Приклад розбивки масиву експериментальних даних на класи та обчислення частот.
2. Масив експериментальних вихідних даних
Для побудови гістограми по осі абсцис відкладають у вибраному масштабі інтервали класів " від" і " до" , а по осі ординат пропорційно частотам висоти прямокутників. Гістограма зображує диференційний закон розподілення випадкової величини.
Для побудови полігону розподіл; / по осі абсцис відкладають значення випадкової величини, а по осі ординат - значення величини, пропорційної накопиченій частоті. Сума ординат дорівнює одиниці. Всі данні для побудови беруть із табл. 3.
3. Таблиця прийнятих класів та знайдених за формулами частот
| № класу, і
| Межі інтервалів класів
| Середини інтервалів, Zi
|
Частота | ||
| абсолютна Bi | відносна bi | накопичена biн | |||
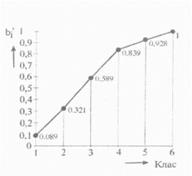
| Від 165 до 169 викл. | 0, 089 | 0, 089 | |||
| Від 169 до 173 викл. | 0, 232 | 0, 321 | |||
| Від 173 до 177 викл. | 0, 268 | 0, 589 | |||
| Від 177 до 181 викл. | 0, 250 | 0, 839 | |||
| Від 181 до 185 викл. | 0, 089 | 0, 928 | |||
| Від 185 до 189 вкл. | 0, 072 | 1, 00 | |||
Для побудови гістограми по осі абсцис відкладають у вибраному масштабі інтервали класів " від" і " до" , а по осі ординат пропорційно частотам висоти прямокутників. Гістограма зображує диференційний закон розподілу випадкової величини. Графічне зображення побудованих частот наведено на рис. 3.
Порядок виконання роботи
1. На окремому аркуші робочого зошита (бажано на міліметровому папері) намалювати заданий викладачем варіант осцилограми.
2. Кількість відрізків Л вздовж горизонтальної осі взяти в межах 40 -50 штук.
|
|
3. Заміряти і записати величину кожної з ординат, тобто утворити масив даних.

| 
|
| а) | б) |
Рис. 3. Графічне зображення частот: а) гістограма та полігон; б - кумулятивна лінія
4. Визначити кількість класів за формулою (1).
5. Визначити інтервал класів за формулою (2).
6. Провести розбивку отриманого експериментального масиву даних на класи та обчислити частоти і записати всі отримані результати згідно з наведеною табл. 1.
7. Побудувати гістограму, полігон та кумулятивну лінію.
8. Визначити математичне сподівання випадкового процесу за
формулою:
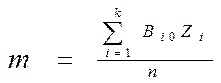

9. Вивчити середнє квадратичне відхилення випадкового процесу за формулою:
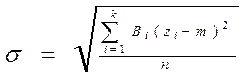
10. Визначити коефіцієнт варіації ( у відсотках ) за формулою:
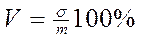
11. Знайти середню помилку досліду згідно з наведеним виразом:
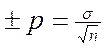
Контрольні запитання
1. Пояснити суть термінів " реалізація", " ансамбль реалізацій", " осцилограма".
2. Як виконати дискретизацію випадкового процесу?
3. Пояснити порядок розподілу масиву даних на класи.
4. Як визначити абсолютну, відносну та накопичену частоти?
5. Як побудувати гістограму та кумулятивну лінію. Які висновки можна зробити про процес залежно від вигляду цих графіків?
6. Що таке полігон розподілу випадкової величини?
7. Навести приклад кумулятивної лінії значень випадкової величини.
Лабораторна робота № 5
Перевірка гіпотези про нормальний розподіл експериментальних
даних
Мета роботи: закріпити знання з методів перевірки гіпотези відповідності емпіричного розподілу випадкової величини теоретичному та навчитись визначати адекватність емпіричного розподілу результатів експериментальних досліджень теоретичному.
Теоретичні відомості
Випадковою величиною називається величина, яка в результаті досліду може приймати будь-яке різне значення. Нехай випадкова величина задана теоретичним законом розподілу, при цьому для кожного значення випадкової величини відома частота 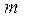 повторюваності або накопичена частота, яка отримана із N дослідів. При
повторюваності або накопичена частота, яка отримана із N дослідів. При 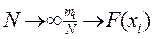

Основними параметрами теоретичних розподілів є математичне сподівання МХ (центр групування) і дисперсія DХ (величина розсіювання).
Для дискретної випадкової величини, коли випадкові величини знаходяться в визначеному інтервалі, у загальному випадку:
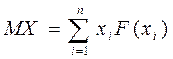 , а
, а 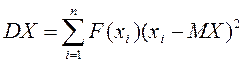
при цьому 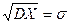 , що називається середнім квадратичним відхиленням теоретичного розподілу. Середнє значення теоретичного розподілу випадкової величини х характеризує центр групування значень випадкової величини.
, що називається середнім квадратичним відхиленням теоретичного розподілу. Середнє значення теоретичного розподілу випадкової величини х характеризує центр групування значень випадкової величини.
У ряді задач виникає потреба в оцінці випадкового розходження між теоретичними і експериментальними параметрами розподілів, тобто між МХ і 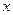 ,
, 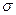 і S - експериментальним середнім квадратичним відхиленням та іншими критеріями оцінок.
і S - експериментальним середнім квадратичним відхиленням та іншими критеріями оцінок.
Така необхідність виникає, наприклад, в наступних випадках:
1)до досліду теоретично розраховані величини МХ і 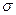 . За результатами вибірки необхідно перевірити правильність теоретичних підрахунків;
. За результатами вибірки необхідно перевірити правильність теоретичних підрахунків;
2)виходячи із ряду технологічних та інших факторів, робиться припущення про чисельні значення параметрів розподілу. Обґрунтування цього припущення піддається перевірці за допомогою експериментальних даних;
3)якщо вже відомі основні параметри і характеристики розподілу, то тоді робляться вибірки через певні проміжки часу. Вирахувані потім експериментальні характеристики зрівнюються з теоретичними.
Після того, як експериментальна крива вирівняна за теоретичною, необхідно знайти вірогідність того, що досліджувана експериментальна крива відповідає вибраному теоретичному закону.
Перевірка гіпотези про нормальний розподіл вибіркової сукупності випадкової величининеобхідна для підтвердження або відхилення нульової гіпотези про розподіл випадкової величини та належність вибіркової сукупності до генеральної. В термін " гіпотеза" в даному випадку вкладається припущення, яке належить до об'єктивних властивостей явища, що вивчається, та підлягає перевірці.
Для нормального закону розподілу випадкової величини найбільш повно розроблені статистичні методи. Тому при відповідності емпіричного розподілу нормальному закону можна максимально використати всі статистичні методи обробки результатів експерименту. При відхиленні гіпотези про нормальний розподіл випадкової величини необхідно визначити закон, до якого ближче знаходиться розподіл результатів експерименту, та використати статистичні методи, розроблені для іншого закону розподілу.
Перевірка відповідності розподілу випадкової величини нормальному закону розподілу може бути проведена за кількома критеріями відповідності: критерієм узгодження Пірсона 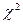 , критерієм Колмогорова к(
, критерієм Колмогорова к( 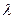 . ), Романовського, сав і т. д.
. ), Романовського, сав і т. д.
У загальному випадку щільність імовірності розподілу випадкової величини для нормального закону має вигляд:

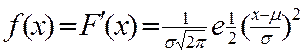 ,
,
де F'(х) - похідна функції розподілу випадкової величини;
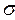 - середнє квадратичне відхилення теоретичного розподілу;
- середнє квадратичне відхилення теоретичного розподілу;
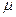 = МХ - математичне сподівання теоретичного розподілу.
= МХ - математичне сподівання теоретичного розподілу.
Перевірка відповідності експериментального розподілу теоретичному за критерієм Пірсона 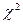 полягає у визначенні величини
полягає у визначенні величини 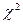 та співставленні її з критичним значенням
та співставленні її з критичним значенням 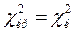 яке знаходять з таблиць для відповідного значення імовірності
яке знаходять з таблиць для відповідного значення імовірності 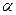 (імовірність практично неможливих випадків) та кількості ступенів відносності
(імовірність практично неможливих випадків) та кількості ступенів відносності 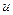 . Критерій Пірсона
. Критерій Пірсона 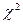 визначається за формулою:
визначається за формулою:
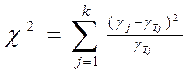
де 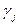 - емпіричні абсолютні частоти трапляння випадкової величини в певний інтервал;
- емпіричні абсолютні частоти трапляння випадкової величини в певний інтервал;
k - кількість класів розрядних частот;
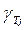 - теоретична частота.
- теоретична частота.
Гіпотеза про розподіл приймається у випадку, коли 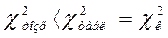 .
.
Критерій Пірсона необхідно застосовувати в тих випадках, коли теоретичні значення параметрів функцій розподілу невідомі. Він забезпечує мінімальну похибку в прийнятті неправильної гіпотези порівняно з іншими критеріями.
Критерій відповідності Колмогорова К( 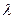 ) базується на знаходженні максимального абсолютного значення різниці між теоретичною fm(x) та емпіричною f(x) функціями розподілу
) базується на знаходженні максимального абсолютного значення різниці між теоретичною fm(x) та емпіричною f(x) функціями розподілу 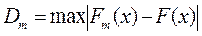 і застосовується, якщо відомі теоретичні значення параметрів. За величиною d знаходять емпіричне значення критерію Колмогорова К(
і застосовується, якщо відомі теоретичні значення параметрів. За величиною d знаходять емпіричне значення критерію Колмогорова К( 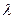 ):
):
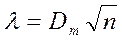 .
.
Порівнявши експериментальні значення функції частот fm(x) зі значеннями теоретичної безперервної функції розподілу F(x), якою проводять вирівнювання, та знайшовши найбільше абсолютне значення різниці між ними D (0)m, складають вираз: 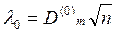 .
.
Для цього 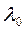 знаходять значення
знаходять значення 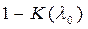 по таблицях. Якщо величина
по таблицях. Якщо величина 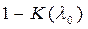 , знайдена за таблицями, мала для даного
, знайдена за таблицями, мала для даного 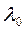 при прийнятому рівні значимості, то нульова гіпотеза приймається.
при прийнятому рівні значимості, то нульова гіпотеза приймається.
Критерії Пірсона та Колмогорова застосовуються для визначення відповідності розподілу випадкової величини для сукупності, яка має велику кількість значень об'єму вибірок (n > 50).
Для невеликих вибірок (n < 12) можна перевірити нормальність розподілу за величиною середнього абсолютного відхилення (CAB):
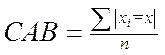
де 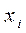 - значення випадкової величини з ряду x1, x2, …., xn;
- значення випадкової величини з ряду x1, x2, …., xn;
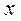 - середнє значення випадкової величини;
- середнє значення випадкової величини;
n - кількість значень випадкової величини.
Для вибірки, яка має приблизно нормальний розподіл повинен бути справедливим вираз:
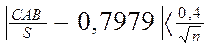
де S - експериментальне середньоквадратичне відхилення випадкової величини.
Порядок виконання роботи
1. Обчислити кількість класів k вибіркової сукупності випадкової величини за формулою 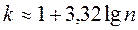 . Отримане число закруглити до цілого в більшу сторону.
. Отримане число закруглити до цілого в більшу сторону.
2. Обчислити ширину кожного класу d для визначеної кількостi класів вибіркової сукупності за формулою: 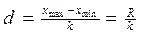 ,
,
де R - статистичний розмах випадкової величини;
 - відповідно максимальне та мінімальне значення випадкової величини.
- відповідно максимальне та мінімальне значення випадкової величини.
3. Розбити вибіркову сукупність випадкової величини на класи, включаючи до них значення величин таким чином: до першого класу від xmin до xmin + d, до другого - від xmin + d до xmin + 2d, до третього – від xmin + 2d до xmin + 3d і так далі. Розбивку на класи слід виконати так, щоб одне і теж значення не було записано двічі.
4. Визначити середні значення для кожного j – гo класу за формулою:
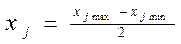
де X j max та X j min - відповідно максимальне та мінімальне значення випадкової величини, яка потрапила в певний клас.
5. За одержаними даними побудувати гістограму розподілу випадкової величини, відкладаючи по осі ординат nj (кількість значень, які потрапили в певний інтервал) для кожного j-го класу з середнім значенням, а по осі абсцис середні значення величини для кожного j-го класу та ширину цього класу.
6. Перевірити, чи відповідає розподіл вибіркової сукупності випадкової величини нормальному закону за CAB, враховуючи що:
середнє значення вибіркової сукупності випадкової величини визначаються за формулою:
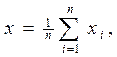 i = 1, 2, …., n
i = 1, 2, …., n
середньоквадратичне відхилення визначається за формулою:
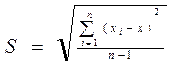
Звіт
Звіт повинен вміщувати:
1. Перевірку нормальності розподілу випадкової величини за CAB.
2. Побудовану гістограму частостей розподілу експериментальних даних для визначеного числа класів k.
3. Розрахунки провести для ряду експериментальних даних згідно з варіантом, (додаток 3), за критерієм CAB.
Контрольні запитання
1. Що таке випадкова величина?
2. Назвіть основні параметри теоретичних розподілів.
3. Як визначається математичне сподівання та дисперсія?
4. Дати визначення критеріїв відповідності.
5. Для яких вибірок застосовується критерій CAB?
Лабораторна робота № 6
Методика планування і проведення багатофакторного експерименту
Мета роботи: вивчити методику планування і проведення повного факторного експерименту та обробки результатів експерименту з використанням статистичних методів і регресійного аналізу.
Теоретичні відомості
Експеримент є основним методом наукових досліджень. В більшості випадків експерименти багатофакторні, тобто на об'єкт дослідження діє два і більше фактори - незалежні змінні величини, які впливають на вихідну величину (параметр оптимізації об'єкту дослідження). Наприклад, дослідження залежності тягового опору плуга (параметр оптимізації ) від таких факторів як швидкість руху, вологість і щільність фунту.
Дослідження об'єкта може здійснюватись класичним методом або методом планування експерименту.
Класичний багатофакторний експеримент - це послідовність одно-факторних експериментів, при яких всі незалежні змінні величини (фактори), крім однієї, приймаються постійними. Наприклад, при дослідженні впливу на тяговий опір плуга швидкості його руху, щільності і вологості ґрунту проводиться ряд класичних експериментів, в першому із яких приймають швидкість руху змінною, а щільність і вологість ґрунту постійними; в наступному експерименті приймають змінною щільність ґрунту, а вологість та швидкість руху постійними і т. д.
Такий шлях досліджень призводить до постановки великої кількості експериментів і при цьому не завжди коректним є допущення можливості стабілізації всіх змінних факторів при послідовному виділенні одного з них, тобто неможливо визначити характер взаємодії факторів між собою і їх сумісний вплив на об'єкт. Ефект взаємодії означає, що вплив одного фактора на параметр оптимізації залежить від того, яке значення приймають інші фактори.
Вираз «планування експерименту» не означає організацію проведення експериментальних досліджень у загальноприйнятому розумінні, що передбачає виконання певного об'єму робіт за періодами часу. Планування експерименту - це метод побудови математичних моделей об'єктів досліджень. При цьому передбачається зміна всіх досліджуваних факторів за певним планом з урахуванням їх взаємодії. Планування експерименту значно підвищує точність і зменшує об'єм експериментальних досліджень.
В експериментальних дослідженнях об'єкт дослідження схематично можна уявити у вигляді так званого «чорного ящика», який може мати n – 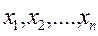 і k –
і k – 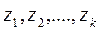 входів і m виходів
входів і m виходів 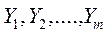 (рис. 1).
(рис. 1).
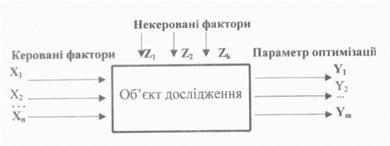
Рис. 1. Схема об'єкта дослідження (" чорного ящика" )
Входами можуть бути зовнішні для об'єкта дослідження впливи чи параметри самого об'єкта. Вихідними величинами можуть бути стани чи параметри - кількісні чи якісні характеристики об'єкта. Наприклад, при дослідженні процесу роботи посівної секції сівалки СУПН-8А входами можуть бути швидкість руху сівалки і частота обертання висівного диска, а виходом - рівномірність розподілу насіння вздовж рядка.
Залежно від умов задачі вихідна величина називається відгуком, функцією відгуку, параметром оптимізації і т. д.
Як правило, аналітичний зв'язок між входом і виходом (модель об'єкта дослідження) невідомий, а відомі фактори і вихідні величини. Вихідну величину, що є невідомою функцією факторів, можна визначити як:
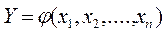 . (1)
. (1)
У цьому випадку задачею планування експерименту може бути побудова математичної моделі об'єкта у вигляді аналітичного виразу:
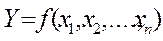 (2)
(2)
який в області можливих значень факторів x1, x2, …., xn досить точно збігається з невідомою залежністю (1).
У багатофакторному експерименті на об'єкт дослідження діє два і більше вхідних факторів, які в ході експерименту варіюють, тобто приймають різні значення своїх величин.
Значення величин, які фактори приймають при варіюванні в експерименті, називаються рівнями факторів. Наприклад, в експерименті швидкість руху орного агрегату знаходилась в межах V = 1, 6 - 3, 0 м/с. У цьому випадку говорять, що фактор варіює на двох рівнях - менше значення (V = 1, 6 м/с) називається нижнім рівнем фактора, а більше значення (V =3, 0 м/с) - верхнім рівнем фактора. Фактори можуть варіювати як на двох, так і на трьох рівнях, але, як правило, завжди приймають два основних рівня варіювання.
Експеримент, в якому реалізуються всі можливі комбінації рівнів факторів, називається повним факторним експериментом і позначають як ПФЕ.
Побудова математичної моделі об'єкта з застосуванням планування експерименту здійснюється наступним чином.
Кількість дослідів при плануванні ПФЕ у загальному випадку визначають за формулою:
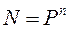 (3)
(3)
де: Р - кількість рівнів;
n - кількість факторів.
Взявши, наприклад, варіант, коли на об'єкт дослідження діють два фактори, які варіюють на двох рівнях, тобто двофакторний експеримент, що позначається як експеримент типу ПФЕ22, можемо записати: 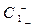 ,
, 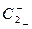 - нижній рівень факторів,
- нижній рівень факторів, 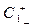 ,
, 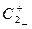 - верхній рівень факторів: де С1, С2 - діючі на об'єкт дослідження фактори в натуральних величинах.
- верхній рівень факторів: де С1, С2 - діючі на об'єкт дослідження фактори в натуральних величинах.
При поєднанні двох факторів на двох рівнях кількість дослідів згідно з формулою (3) буде дорівнювати: N = 22 = 4. При кожному наборі факторів (у кожному окремому досліді) вимірюється відгук Y, в результаті чого отримуємо чотири точки Y1, Y2, Yз, Y4 , які утворюють поверхню
відгуку, зображену на рис. 2
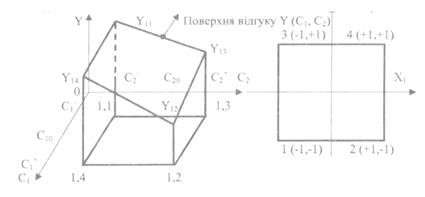
| Рис. 2. Результати двофакторного експерименту | Рис. 3. Область експерименту для кодованих факторів |
Для кожного експерименту необхідно вибрати інтервал варіювання, яким називається половина різниці між більшим ( верхнім ) і меншим ( нижнім ) значенням фактора. Значення кожного фактора С1 і С2 в центрі області експерименту називається його основним рівнем і помічається індексом «О», тобто С10 та С2о ( рис. 2).
Для зручності запису плану експерименту і обробки експериментальних даних користуються кодованими значеннями факторів, які є
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|