lg yi = lg a + xi lg b = 0.6789 + xi *0.03216

Вступ

Вивчення технологій і робочих процесів сільськогосподарських машин, а також розробка нових машин, технічних ліній і складних сільськогосподарських комплексів та практичне використання методів їх оптимальної експлуатації вимагають від інженерних кадрів глибокого засвоєння наукових методів аналізу і синтезу сучасних об'єктів, технологічних і виробничих процесів.

У даний час, коли розвиток механізації сільськогосподарського виробництва вимагає нових підходів і технічних рішень, молоді спеціалісти повинні опанувати сучасні методи і принципи проведення наукових досліджень.

Принциповою особливістю системного підходу до проблем сільського господарства є прагнення врахувати весь комплекс факторів, які визначають розвиток галузі. Саме комплекс тісно пов'язаних організаційних, економічних, технологічних та інших засобів, їх глибоке вивчення в поєднанні з моделюванням сільськогосподарських процесів являє собою основу системного підходу до вирішення найбільш широких наукових проблем.

Програма предмету " Основи наукових досліджень" передбачає виконання лабораторних робіт з метою більш глибокого засвоєння теорії методології і наукових методів та принципів проведення досліджень в області механізації сільськогосподарського виробництва і розвитку творчого мислення студентів.

Задачі курсу - дати знання з основ організації наукових досліджень, поняття про теоретичні і експериментальні методи дослідження, методи побудови математичних моделей, планування і проведення багато факторних експериментів та обробки і аналізу отриманих результатів.

Лабораторні роботи виконуються студентами самостійно на практичних заняттях під керівництвом викладача. В кожній роботі визначена її мета, викладені теоретичні передумови, порядок виконання і оформлення результатів та аналізу виконаних наукових робіт.

При виконанні кожної лабораторної роботи студент спочатку вивчає теоретичні передумови, виконує необхідні математичні розрахунки за приведеними формулами, заповнює таблиці, будує відповідні графічні залежності ( графіки, діаграми і т. п. ) і відповідним чином оформлює звіт, який потім пред'являється викладачу для перевірки і захисту. За кожну виконану лабораторну роботу студент отримує відповідну оцінку. Викладений матеріал може бути використаний як навчальний посібник для студентів факультету МСГ НАУ.

Лабораторна робота № 1

Визначення коефіцієнтів і сталих лінійних емпіричних залежностей.

Мета роботи: вивчити порядок обчислення невідомих коефіцієнтів і сталих емпіричних залежностей, які описують поведінку отриманого експериментального масиву даних способами обраних точок, середніх та найменших квадратів.

Теоретичні відомості

При проведенні експериментальних досліджень досить часто необхідно встановити, як впливає зміна вхідного факторах, наприклад, щільність ґрунту на вихідний процес у, наприклад тяговий опір плуга, тобто визначити теоретичну залежність, яка б описувала поведінку досліджуваного процесу, або вибрати математичну функцію у = f(x), яку, як правило, називають математичною моделлю об'єкта дослідження.

Визначити функцію у = f(x) або математичну модель об'єкта дослідження можна за результатами проведених пасивних (однофакторних) експериментів. Експеримент називають пасивним або однофакторним тоді, коли в кожному окремому досліді змінюють послідовно один вхідний діючий фактор при постійних значеннях всіх інших. У обраному нами випадку діє один фактор х. Тому, якщо в ході експерименту задавати цьому факторові значення x_1,x_2,…., x_N, то отримаємо відповідні значення функції у₁, y₂…. y_N_, де N - кількість проведених дослідів в експерименті або так званий масив експериментальних даних.

Коли між діючим фактором х і відповідними змінними значеннями функції у існує лінійна математична залежність, то в простішому випадку її можна описати лінійним рівнянням виду у = а + bх, де а та b - сталі невідомі коефіцієнти даного рівняння.

Вибране лінійне рівняння ще називають емпіричною формулою.

Задача зводиться до визначення невідомих коефіцієнтів а та b вибраної емпіричної формули. Ці коефіцієнти визначаються за результатами проведених дослідів. Наприклад, при проведені однофакторного експерименту при N = 8 отримали такий масив значень експериментальних даних:

N, кількість дослідів
x, щільність ґрунту
y, тяговий опір плуга

Визначимо за цими отриманими експереме6нтальними даними коефіцієнти a та b емпіричної формули y = a + bx, яка описує поведінку отриманих експериментальних даних.

1. Спосіб обраних точок

Визначення невідомих коефіцієнтів за способом обраних точок полягає в довільному вибору з масиву експериментальних даних такої кількості точок (відповідних значень x та y), яка б дорівнювала кількості невідомих коефіцієнтів вибраної математичної моделі, тобто теоретичної залежності y = f (х).

Оскільки у нашому випадку, вибрана нами емпірична формула y = a + bx має два невідомих коефіцієнти, то для їх визначення необхідно скласти систему двох лінійних рівнянь: y₁ = a + bx₁ та y₂ = a + bx₂ ,

де x₁_, x₂ - значення фактора, які відповідають вибраним точкам;

y₁_, y₂ - значення функції, які відповідають вибраним точкам.

Наприклад, з наведеного масиву значень експериментальних даних, довільно обираємо два значення вхідного фактора: x₁ = 15, y₁ = 101 - перша експериментальна точка, x₂ = 50, y₂ = 334 - відповідно друга експериментальна точка.

Тоді складаємо систему двох лінійних рівнянь:

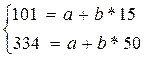
Після математичного розв'язання цієї системи маємо: а = 1, 1; b = 6, 66. Таким чином, емпірична формула, що описує поведінку експериментальних даних, матиме вигляд: у = 1, 1 + 6, 66х.

Як бачимо, спосіб обраних точок дуже простий, але неточним, бо для визначення коефіцієнтів ми використали з усього масиву даних лише дві пари значень х та у.

2. Спосіб середніх

Спосіб середніх полягає в тому, що невідомі коефіцієнти емпіричної залежності визначаються з умови прирівнювання до нуля різниці суми всіх відхилень дійсних отриманих практичних значень експерименту, тобто величини y_i від отриманих обчислень у_i₀ , які вирахували згідно з вибраною теоретичною залежністю:

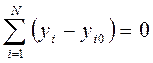
Для залежності виду y = a + bx маємо:

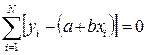
Після перетворень отримаємо:

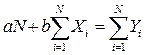
Таким чином, ми маємо одне рівняння, але з двома невідомими а та b.

Щоб розв'язати поставлену задачу, необхідно поділити весь масив експериментальних даних на стільки частин, скільки невідомих у рівнянні. У даному - на дві частини:

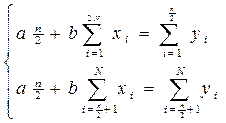
Для наведених експериментальних даних маємо:

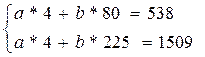
Після розв'язання системи лінійних рівнянь емпірична формула, яка описує поведінку експериментальних даних, матиме вигляд:

у = 0, 58 + 6, 7х.

При визначенні коефіцієнтів а та b способом середніх ми використали весь масив даних. Але цей спосіб ефективний лише у тих випадках, коли кількість невідомих коефіцієнтів, що входять в емпіричну формулу, не перевищує 1 чи 2, максимум - 3. Тому розглянемо найбільш поширений і точний спосіб визначення невідомих коефіцієнтів.

3. Спосіб найменших квадратів

Суть цього способу полягає в тому, що сума квадратів відхилень експериментальних даних у_i від y_i₀ які визначені за формулою вздовж осі ординат ОY, повинна бути мінімальною - принцип Лежандра. Відповідно до цього принципу часткові похідні від функції 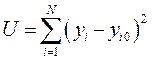по кожному з невідомих коефіцієнтів повинні дорівнювати нулю.

Для нашого випадку при вибраній емпіричній формулі y = a + bx маємо:

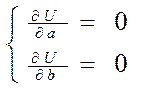де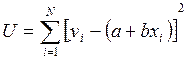

Тоді можемо записати:

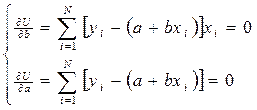
або після перетворення отримаємо:

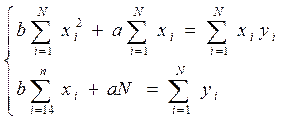
Після розв'язання системи рівнянь за наведеними значеннями експериментальних даних отримаємо: а = 0, 04; = 6, 71.

Тоді емпіричне рівняння матиме: y = 0, 04 + 6, 71х.

Порядок виконання роботи.

1. Побудувати таблицю вихідних даних та результатів обчислень у вигляді ( варіанти завдань взяти згідно з додатком 1):

i	x_i	y_i	x_i y_i	x²_i
.. n

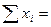
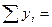
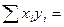
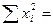
2. Вважати, що зміна вихідного параметра експериментальних даних
описується лінійною залежністю виду y = a + bx.

3. Обчислити невідомі коефіцієнти а та b за трьома способами:

обраних точок, середніх, найменших квадратів.

4. Записати отримані кожним із способів кінцеві емпіричні формули.

5. На координатній площині ХОУ побудувати графіки згідно з отриманими теоретичними емпіричними формулами типу для y = a + bx кожного із використаних способів. На цій же координатній площині ХОУ побудувати графічну залежність заданого масиву експериментальних даних у вигляді ламаної лінії. Кожну з ліній на графіку виконати в іншому стилі (кольорі) і позначити.

Контрольні запитання

1. Який експеримент називається пасивним?

2. Скільки необхідно взяти довільних точок при визначенні невідомих коефіцієнтів способом обраних точок, коли у вибраній математичній залежності їх буде 3 або 5?

3. У чому полягає суть визначення невідомих коефіцієнтів способом найменших квадратів?

4. Дати визначення поняттю " масив експериментальних даних".

Лабораторна робота № 2

Визначення виду та параметрів емпіричних залежностей

Мета роботи: більш глибоко засвоїти поняття апроксимації отриманої експериментальної залежності та етапи і порядок визначення виду емпіричних формул та аналізу результатів отриманих робіт.

Теоретичні відомості

Після проведення експерименту дослідник отримує ряд статистичних величин (масив експериментальних даних), коли кожному наданому їм в експерименті значенню вхідного фактора x_1,x_2,…., x_N відповідає певне значення вихідної досліджуваної величини (функції) або параметру оптимізації у₁, y₂…. y_N_. На підставі аналізу отриманого масиву експериментальних даних можливо підібрати таку математичну залежність у = f (х), яка б описувала поведінку досліджуваних величин факторів та функції, тобто поведінку зміни досліджуваної функції від зміни вхідного фактора. Подібний алгебраїчний вираз, тобто математична залежність, називається емпіричною залежністю або емпіричною формулою, а сам процес підбору - апроксимацією.

Емпіричні формули дають можливість оперативно визначати величину функції, тобто параметра оптимізації залежно від діючого фактора в широкому інтервалі його зміни. Бажано, щоб емпіричні формули були простими, але якомога точніше описували процес, що досліджується. Тому для підбору емпіричних формул використовують здебільшого елементарні функції, а для визначення коефіцієнтів та сталих цих функцій застосовують найбільш поширений спосіб - найменших квадратів.

Процес підбору емпіричних формул складається з двох етапів:

i етап. Дані експерименту наносять на Декартову систему координат, з'єднують отримані точки ламаною лінією і підбирають орієнтовно вигляд математичної залежності (моделі, формули) об'єкта дослідження.

ii етап. Обчислюють невідомі коефіцієнти та сталі, що входять до обраної математичної формули.

Розглянемо методику визначення невідомих коефіцієнтів основних елементарних функцій.

Графіки основних елементарних функцій наведені на рис. 1 та рис. 2.

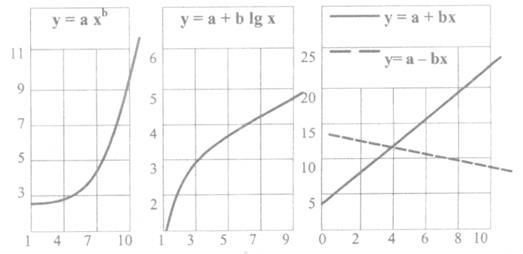
а б в

Рис. 1. Графіки степеневої (а), логарифмічної (б) та прямо пропорційної
(в) функцій

а б в

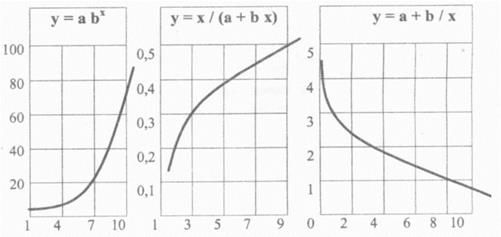
Рис. 2. Графіки показової (а) та зворотно пропорційних функцій (б, в).

1. Показова функція

Рівняння показової функції має вигляд: 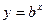або 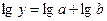. Невідомі коефіцієнти а та b, що входять до емпіричної формули, визначаються за формулами:

;

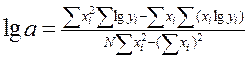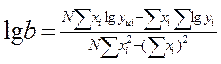
Наприклад, у результаті обчислень отримали lg a = 0. 6789, а lg b = 0, 03216, звідки знайшли, що а = 4, 77; b = 1, 08. Тоді емпірична формула буде мати вигляд: у = 4, 77 * 1, 08^х.

Знаходимо теоретичне значення апроксимованої кривої за формулою:

lg yi = lg a + xi lg b = 0. 6789 + xi *0. 03216

де x_i - експериментальне значення і -го досліду.

2. Степенева функція

Рівняння степеневої функції має вигляд: у = ах^b або lg у = lg а + b lgx

Невідомі коефіцієнти а та b, що входять до емпіричної формули, визначаються за формулами:

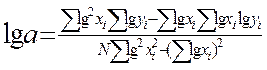
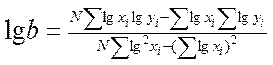
Подальший порядок проведення розрахунків аналогічний порядку п. 1 (показова функція).

3. Логарифмічна функція

Рівняння логарифмічної функції має вигляд: y= a + b lg x.

Невідомі коефіцієнти а та b, що входять до емпіричної формули можуть визначаються за формулами:

;

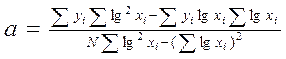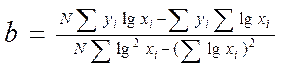
Подальший порядок проведення розрахунків невідомих коефіцієнтів а та b аналогічний порядку п. 1 (показова функція).

Коефіцієнти та сталі, які входять до останніх емпіричних формул визначаються із системи нормальних рівнянь, отриманих способом найменших квадратів і наведених в табл. 1.

Вихідне рівняння	Система нормальних рівнянь

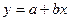
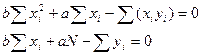
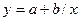
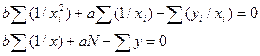
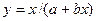
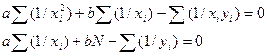
Знак 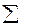, наведений у формулах таблиці дня визначення невідомих коефіцієнтів а та b, означає суму експериментальних значень (вихідних даних для проведення розрахунків) від і = 1 до N, де і - порядковий номер досліду в експерименті; N - кількість проведених повторностей (дослідів) в експерименті.

Розв'язати систему нормальних рівнянь відносно невідомих коефіцієнтів а та b можна виконати будь- яким загальноприйнятим способом.

При виконанні першого етапу може виникнути такий випадок, що для апроксимації експериментальних даних за своєю графічною побудовою (виглядом) орієнтовно підходять дві чи три функції. Тому для оцінки ступеня точності вирівнювання (апроксимації), побудованої графічної залежності за результатами отриманих експериментальних даних, тією чи іншою вибраною апроксимуючою функцією, необхідно визначити величину так званої " нев'язки" 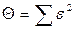, тобто сумарне середньоквадратичне відхилення теоретичних значень, обчислених за визначеною емпіричною формулою від експериментальних значень проведеного досліду для кожної з вибраних для проведення апроксимації формул. Величина " нев'язки" визначається за формулою:

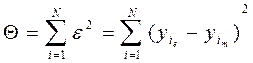
де 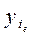- експериментальні значення і-го досліду;

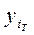- теоретичне значення і-го досліду, визначеного за одержаною емпіричною формулою.

Для подальшого використання залишають те емпіричне рівняння, для якого величина " нев'язки" 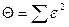найменша за числовим значенням, де знак 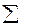означає суму квадратів 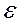від і = 1 до N, де .

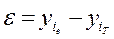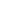
Приклад. Підібрати емпіричну формулу для такого масиву експериментальних даних, де кількість повторностей в експерименті дорівнює 8.

x
y

Наносимо точки експериментальних даних на координатні осі і будуємо ламану лінію, тобто графік експериментальної залежності (рис 3).

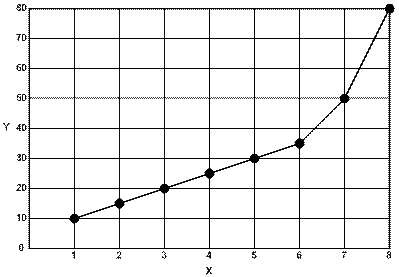
Рис 3. Експериментальна залежність

Орієнтовно, для описання поведінки побудованих експериментальних точок (експериментального масиву даних) обираємо дві функції: лінійну виду 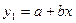та другого порядку 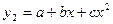, тобто відповідно пряму лінію та параболу. Після визначення методом найменших квадратів невідомих коефіцієнтів а, b, та с, що входять до цих формул, записуємо одержані емпіричні формули:

;

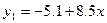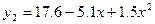
Перевіримо, яка з одержаних емпіричних формул 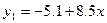та 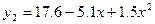, краще апроксимує (описує, вирівнює) побудовану експериментальну залежність, наведену на рис. 3. Для цього визначимо показники, які наведені в табл. 2, і занесемо до неї результати цих обчислень.

2. Результати апроксимації експерементальних даних

N	Експериментальні дані X та Y і розрахунок вихідних даних	Апроксимація
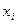
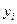
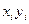
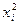
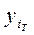
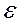
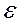	Експериментальні дані X та Y і розрахунок вихідних даних
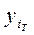
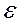
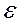				²			²
		3, 4	6, 6	43, 6
		11, 9	3, 1	9, 6	13, 4	1, 6	2, 56
		19, 5	0, 4	0, 16	15, 8	4, 2	17, 6
		23, 4	3, 9	15, 2	21, 2	3, 8	14, 4
		37, 1	7, 1	50, 4	29, 6	0, 4	0, 16
		45, 5	10, 5	110, 2
		54, 4	4, 4	19, 4	55, 4	5, 4	29, 1
		62, 9	17, 1	282, 4	72, 8	7, 2	51, 8
		259, 1	53, 1	540, 9	259, 2	32, 6	167, 6

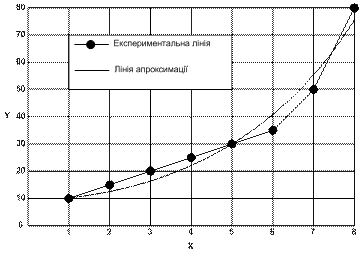
Рис. 4. Результати апроксимації експериментальних даних

Як бачимо, величина " нев'язки" 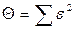для параболи становить 167, 6, а для прямої – 540, 9, тобто апроксимація параболою більш точно описує або вирівнює експериментальну криву.

На рис. 4 зображено графік експериментальної залежності у вигляді ламаної лінії, точки якої побудовані за значеннями експериментального масиву даних та вибраної емпіричної залежності 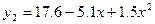, яка апроксимує експериментальну.

Порядок виконання роботи

1. Записати вихідні дані для проведення розрахунків (експериментальний масив даних згідно з додатком 2).

2. Нанести експериментальні точки на координатну площину ХОУ і з’єднати їх відрізками прямих (побудувати експериментальну ламану лінію).

3. Виходячи з вигляду експериментальної ламаної лінії, підібрати орієнтовно дві аналітичні залежності (функції), які приблизно описують побудований графік експериментальної залежності.

4. Для кожної з вибраних аналітичних залежностей визначити невідомі коефіцієнти в такій послідовності:

4. 1. Визначити та записати систему нормальних рівнянь з табл. 1;

4. 2. Розв'язати вибрану систему нормальних рівнянь відносно невідомих коефіцієнтів;

4. 3. Підставити значення коефіцієнтів у формули і записати емпіричні формули в остаточному вигляді.

5. Встановити, яка з отриманих емпіричних формул краще апроксимує експериментальні дані. Для цього скласти таблицю за формою, подібною до форми табл. 2.

6. Шляхом порівняння " нев'язки" 0 = Је² вибрати необхідну емпіричну залежність.

7. Побудувати за обраною емпіричною формулою теоретичну залежність у = f(x) на тих же координатних осях що і в п. 2 (лінію виконати в іншому стилі чи кольорі, ніж експериментальну ламану).

Контрольні запитання

1. Дати визначення поняттю " масив експериментальних даних".

2. Апроксимація, її суть і призначення.

3. Для чого призначена система нормальних рівнянь?

4. Як визначається величина " нев'язки"?

5. За яким критерієм вибирається емпірична формула для проведення апроксимації експериментальних даних?

Лабораторна робота № 3

Складання учбової заявки на винахід

Мета роботи: вивчити методику складання і оформлення заявки на видачу патенту на винахід та порядок проведення патентного пошуку.

Теоретичні відомості

Важливою сферою діяльності інженерно-технічних та конструкторських працівників є винахідницька та раціоналізаторська робота. Результатом такої роботи є створення нових технологій, машин, обладнання та вдосконалення існуючої техніки та виробничих процесів - тобто об'єктів промислової власності.

Відповідно до " Тимчасового положення про правову охорону об'єктів промислової власності та раціоналізаторських пропозицій в Україні" до об'єктів промислової власності належать винаходи, корисні моделі, промислові зразки, знаки для товарів і послуг, фірмові найменування та позначення походження чи найменування місця походження товарів.

Промислова власність поширюється на промисловість, торгівлю, сільськогосподарське виробництво, продукти промислового чи природного походження.

Правова охорона перших трьох об'єктів здійснюється у формі видачі патентів, наступні два - у формі видачі свідоцтв.

Винаходом вважається нове, що має суттєві відмінності, технічне вирішення задачі в будь-якій області господарства, соціально-культурного будівництва чи оборони країни, який відповідає умовам патентоспроможності, тобто є новим та промислово придатним, і використання якого в народному господарстві дає позитивний ефект. Винахід вирішує задачу у сфері практичної творчої діяльності людини, обумовлену певною соціальною потребою.

Промисловий зразок - результат творчої діяльності людини у галузі художнього конструювання, який відповідає умовам патентоспроможності, тобто є новим і промислово придатним.

Знак для товарів і послуг - позначення, за яким товари і послуги одних осіб відрізняються від однорідних товарів і послуг інших осіб.

Патентоспроможність - це властивість, якої набуває об'єкт господарської діяльності та його складові частини у разі відповідності умовам надання правової охорони винаходу, корисній моделі, промисловому зразку та іншим об'єктам промислової власності згідно з чинним законодавством держави.

Згідно з " Тимчасовим положенням... " технічне вирішення задачі є винаходом, якщо воно має такі ознаки:

- новизну, тобто якщо воно не є частиною існуючого рівня техніки;

- винахідницький рівень, тобто якщо воно для спеціаліста явно не випливає з існуючого рівня техніки;

- промислову придатність, тобто якщо воно може бути використане у промисловості, сільському господарстві, охороні здоров'я та інших галузях народного господарства.

Рівень техніки визначається за всіма джерелами науково-технічної інформації до дати пріоритету.

Об'єктами господарської діяльності або винаходу можуть бути:

- продукт, тобто пристрій, речовина, штам мікроорганізму, культура клітин, рослин і тварин;

- спосіб;

- позначення товарів і послуг;

- застосування відомого раніше пристрою, способу, речовини та штаму за новим призначенням або винахід на застосування.

Пристрій - це конструкції та вироби, наприклад, машина для збирання цукрових буряків, дисковий копач і т. д.

Речовина - це індивідуальні сполуки, композиції, продукти ядерного перетворення, наприклад, фарба, лікарські препарати, металевий сплав і т. д.

Штам мікроорганізму - це чиста культура певного виду мікроорганізмів.

Спосіб - це процес чи процеси виконання дій над матеріальними об'єктами, наприклад, спосіб збирання цукрових: буряків, відновлення зношених деталей і т. д.

Найбільш тісно з діяльністю інженерних працівників сільськогосподарського виробництва пов'язані такі об'єкти винаходу як пристрій і спосіб.

Не вважаються винаходами: наукові теорії; методи організації та управління господарством; умовні позначення, розклади, правила; методи виконання розумових операцій; алгоритми і програми для обчислювальних машин; проекти і схеми планування споруд, будинків, територій; пропозиції, що стосуються лише зовнішнього вигляду виробів і спрямовані на задоволення естетичних потреб.

Право на винахід засвідчується патентом, який визначає авторство та пріоритет винаходу і діє протягом 20 років. Для того, щоб отримати патент на винахід, необхідно скласти і оформити певні документи, які в сукупності складають заявку на видачу патенту на винахід.

Заявка на винахід повинна мати такі документи: заявку на видачу патенту; опис винаходу; формулу винаходу; креслення та інші ілюстративні пояснювальні матеріали, які розкривають і доповнюють суть винаходу; реферат; платіжний документ, який підтверджує сплату мита в установленому розмірі.

Заявка подається до Державного патенту України у трьох примірниках. Заява про видачу патенту подається у спеціально установленій формі.

Опис винаходу має розкривати суть винаходу з повнотою, достатньою для його здійснення, і підтверджувати обсяг правової охорони, визначений формулою винаходу.

Опис винаходу має таку структуру: назва винаходу; клас міжнародної патентної класифікації (МПЖ); галузь техніки, до якої належить винахід; характеристика аналогів винаходу та його прототипу; критика аналогів та прототипу; мета винаходу; перелік фігур графічних зображень; детальний опис винаходу в статичному стані та в процесі роботи.

Назва винаходу - це коротке викладення суті об'єкта винаходу, наприклад: " Робочий орган для викопування коренеплодів", " Дисковий копач", " Спосіб вирощування картоплі" і т. д.

Класифікація винаходів це спеціальна система упорядкування патентних документів, яка розподіляє технічні рішення за тематичними рубриками з метою оперативного пошуку патентної інформації, що відповідають запиту.

За домовленістю ряду європейських країн було розроблено Міжнародну патентну класифікацію. Вона складається із 8 розділів: розділ А - задоволення життєвих потреб людини; розділ В - різні технологічні процеси; розділ С - хімія та металургія; розділ D - текстиль та папір; розділ Е - будівництво; розділ F - прикладна механіка, освітлення і опалення, двигуни і насоси, зброя і боєприпаси; розділ G - технічна фізика; розділ Н - електрика.

Також МПЖ має 118 класів та 617 підкласів, які позначаються великими приголосними літерами. Підкласи поділяються на групи, які позначаються, як правило, непарними цифрами. Групи також розбиваються на підгрупи, які позначаються парними цифрами. Перша підгрупа в кожній групі позначається індексом 00.

Галузь сільського господарства належить до першого розділу А і має загальне позначення А 01, наприклад, А 01 С - посівні машини, а вже А 01 С 7 / 04 - пневматичні сівалки, тобто А - це розділ, 01 - клас сільське господарство, С - підклас посівні машини, 7/04 - відповідно група та підгрупа пневматичні сівалки.

Галузь техніки, до якої належить винахід, - це конкретне визначення області використання винаходу. Наприклад, винахід належить до сільського господарства, конкретно до машин для посіву зернових культур.

Характеристика аналогів винаходу - це детальний аналіз відомих і подібних до нього за технічною суттю та результатом, що досягається при їх використанні об'єктів того ж призначення, як і той, що заявляється. В характеристиці аналогів приводиться критика недоліків, які належать вибраним аналогам.

Характеристика прототипу - це опис, аналіз та критика недоліків найбільш близького за своєю технологічною і технічною суттю аналога. В критиці аналогів і прототипу описуються тільки ті недоліки, які усуваються винаходом.

Мета винаходу - це та позитивна дія, при виконанні якої будуть усунені недоліки прототипу, наприклад, з метою усунення втрат коренеплодів і т. д.

Перелік фігур графічних зображень - це порядкова нумерація всіх графічних матеріалів, які подаються у винаході, наприклад, фіг. 1, фіг. 2 і т. д.

Детальний опис винаходу - це опис загальної будови винаходу та його принципу роботи.

Формула винаходу - коротка, складена за спеціальним правилами і формою словесна характеристика суті технічного рішення винаходу. Вона складається у формі одного речення з певною структурою викладання та визначає обсяг правової охорони, наданої патентом.

Формула винаходу має таку структуру:

- назва винаходу;

- обмежувальна частина, яка включає загальні (спільні) відомі ознаки об'єкта винаходу і прототипу;

- відзначна частина, яка включає нові ознаки, що відрізняють об'єкт винаходу від прототипу і відокремлюється від обмежувальної частини словами, який (яка, яке) відрізняється тим, що... ";

- мета винаходу, яка записується за словом "... що, з метою" , наприклад, " усунення втрат зерна підбарабання встановлено під кутом... " і т. д.

Креслення та інші ілюстративні матеріали подаються у випадку, якщо вони необхідні для розуміння суті викладеного в описі передбачуваного винаходу.

Реферат є по суті скороченим викладом змісту винаходу та має:

- назву винаходу;

- характеристику та галузь техніки, до якої належить передбачуваний винахід, галузь його використання;

- стислу характеристику суті винаходу із зазначенням технічного результату, якого мають досягти.

Патентний пошук - це різновидність інформаційного пошуку, що здійснюється переважно у фондах патентної документації з метою встановлення рівня технічного вирішення, меж прав власника патенту і умов реалізації прав.

Раціоналізаторська пропозиція

Згідно з " Тимчасовим положенням... " раціоналізаторською визнається пропозиція, що є новою і корисною для підприємства, якому вона подається, і передбачає створення або зміну конструкції виробів, технології виробництва застосовуваної техніки або складу матеріалу.

Раціоналізаторська пропозиція є новою для підприємства, якому вона подається, якщо згідно з наявними на даному підприємстві джерелами інформації ця пропозиція не була відома у мірі, достатній для її практичного використання.

Заява на раціоналізаторську пропозицію з описом суті пропозиції подається в письмовій формі підприємству (господарству), на якому передбачається її використання. До заяви додаються схеми, креслення чи ескізи, якщо це необхідно. Представлені матеріали повинні містити дані, достатні для практичного втілення пропозиції.

Підприємство (господарство), яке прийняло до розгляду заяву, повинно її зареєструвати і протягом місяця від дати реєстрації прийняти рішення. При позитивному рішенні автору (авторам) видається посвідчення на раціоналізаторську пропозицію.

Відкриття

Вивчаючи винахідництво та раціоналізаторство як сферу прикладної діяльності треба, мати на увазі, що існує область фундаментальних творчих досліджень і основним, самим цінним і вагомим результатом цих досліджень, є відкриття.

Відкриттям визнається встановлення невідомих раніше об'єктивно існуючих закономірностей, властивостей і явищ матеріального світу, які вносять корінні зміни в рівень пізнання.

Кожне відкриття має певний об'єкт: явище; властивість; закономірність.

Важливо відмітити, що відкриття є основою для багатьох винаходів.

Порядок виконання роботи

1. Ознайомитись в патентному фонді України з порядком пошуку патентної інформації і описати його.

2. Скласти опис і формулу технічного розв'язання задачі (за власним вибором) з області сільськогосподарських машин або вибрати один з патентів (авторських свідоцтв) на винахід з області сільськогосподарських машин з вказаної викладачем групи машин і зробити його аналіз у вигляді наведеної нижче табл. 1.

Рекомендована форма написання звіту

Зміст патенту або авторського свідоцтва: №, клас МПК, назва, опис винаходу (будова, принцип роботи), формула винаходу, анотація і т. д.	Назва розділів опису і складових частин формули винаходу
Наприклад: 123456789 А 01 Д23/04 і так далі за всіма складовими частинами охоронного документу	Номер авторського свідоцтва Клас МПК

12 Следующая ⇒