
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Асимптоты графика функции. Примеры.
Асимптоты графика функции
Опр. Асимптотой графика функции y = f (x) называется прямая линия, обладающая тем свойством, что расстояние от переменной точки на графике до прямой стремится к нулю при неограниченном удалении этой точки по графику от начала координат.
Опр. Прямая х = а является вертикальной асимптотой, если по крайней мере один из односторонних пределов равен ± бесконечности, т. е.
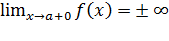 ,
, 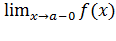 =
= 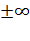 .
.
Опр. Прямая у = с является горизонтальной асимптотой, если предел при
х ®± ¥ равен константе, т. е. 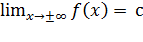
Опр. Прямая у = b х + с является наклонной асимптотой если
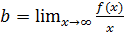 ,
, 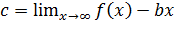
Примеры.
1. Построить график функции 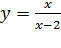 .
.
Найдем область определения функции. Так как функция дробно-рациональная, то знаменатель не обращается в нуль: х – 2 ¹ 0. т. е.
х Î (-¥; 2) È (2; +¥ )
Исследуем функцию в граничных точках.
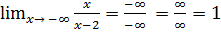 => у =1 - горизонтальная асимптота
=> у =1 - горизонтальная асимптота
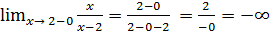 => x = 2 - вертикальная асимптота
=> x = 2 - вертикальная асимптота
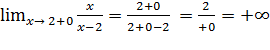 => x = 2 - вертикальная асимптота
=> x = 2 - вертикальная асимптота
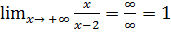 => у =1 - горизонтальная асимптота
=> у =1 - горизонтальная асимптота
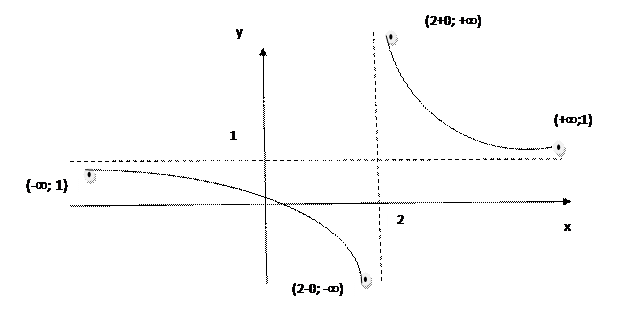
Для построения графика полученные данные занесем в таблицу.
| х | -¥ | 2-0 | 2+0 | +¥ | |
| у | -¥ | разрыв II рода | +¥ |
Нанесем полученные точки на график:
(-¥; 1) (2-0; -¥ ) (2+0; +¥ ) (+¥; 1)
2. Построить график функции 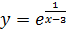 .
.
Найдем область определения функции. Так как показатель функции есть функция дробно-рациональная, то знаменатель не обращается в нуль: х – 3 ¹ 0. т. е. х Î (-¥; 3) È (3; +¥ )
Исследуем функцию в граничных точках.
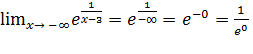 =1 => у =1 - горизонтальная асимптота
=1 => у =1 - горизонтальная асимптота
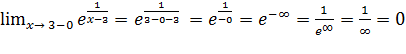 => x = 3 - вертикальная асимптота
=> x = 3 - вертикальная асимптота
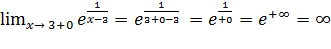 => x = 3 - вертикальная асимптота
=> x = 3 - вертикальная асимптота
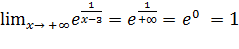 => у =1 - горизонтальная асимптота
=> у =1 - горизонтальная асимптота
Для построения графика полученные данные занесем в таблицу.
| х | -¥ | 3-0 | 3+0 | +¥ | |
| у | разрыв II рода | +¥ |
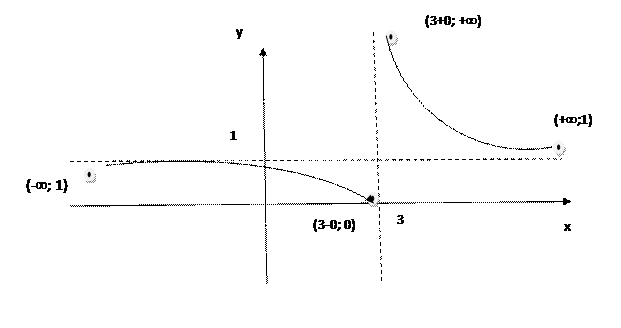
Нанесем полученные точки на график:
(-¥; 1) (3-0; 0) (3+0; +¥ ) (+¥; 1)
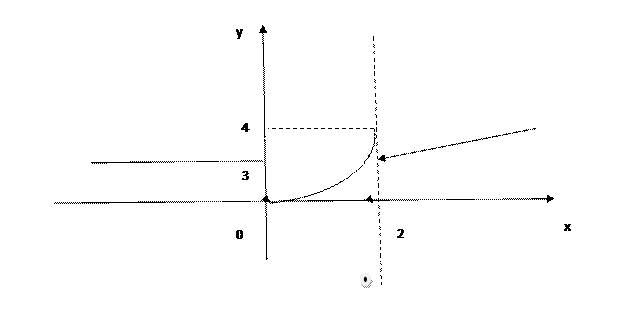
3. 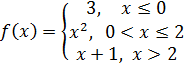
Точки подозрительные на разрыв: х = 0 и х = 2
Вычислим пределы в этих точках
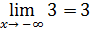
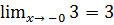
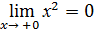
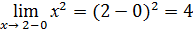
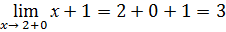
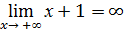
Для построения графика полученные данные занесем в таблицу.
| х | -¥ | -0 | +0 | 2-0 | 2+0 | +¥ | ||
| у | разрыв I рода | разрыв I рода | ¥ |
(-¥; 3) (-0; 3) (+0; 0) (2-0; 4) (2+0; 3) (+¥; ¥ )
Теоремы о непрерывных функциях.
Теорема1. Если функция непрерывна в точке х0 и f(x0) ¹ 0, то существует такая окрестность точки х0 в которой знак функции f(x) совпадает со знаком f(x0).
Дано.
Для " e > 0 $d > 0 такая, что в окрестности (х0 - d; х0 + d) 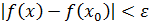 .
.
Доказать.
sign f(x) = sign f(x0), где sign («сигнум»)- знак
Доказательство.
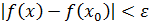 . Распишем модуль.
. Распишем модуль.
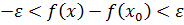 =>
=> 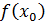
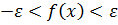 +
+ 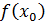
Возьмем в качестве e положительное число 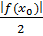 , тогда
, тогда 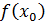
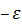 и
и 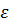 +
+ 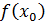 являются положительны при
являются положительны при 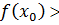 0 и отрицательны при
0 и отрицательны при 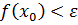 . Т. е. функция
. Т. е. функция 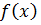 будет заключена, либо между двумя положительными числами. ьогда она будет положительна, либо между двумя отрицательными числами, тогда она будет отрицательна.
будет заключена, либо между двумя положительными числами. ьогда она будет положительна, либо между двумя отрицательными числами, тогда она будет отрицательна.
Теорема доказана.
Теорема 2. Пусть функция 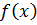 непрерывна на отрезке [a; b] т. е.
непрерывна на отрезке [a; b] т. е. 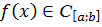 и значения функции на концах отрезка имеют разные знаки т. е sign f(а) ¹ sign f(b). Тогда на отрезке [a; b] найдется точка с, такая что
и значения функции на концах отрезка имеют разные знаки т. е sign f(а) ¹ sign f(b). Тогда на отрезке [a; b] найдется точка с, такая что 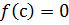 .
.
Дано.
Не ограничивая общности, будем считать, что 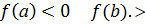 0.
0.
Доказать
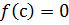 , где с Î [a; b]
, где с Î [a; b]
Доказательство.
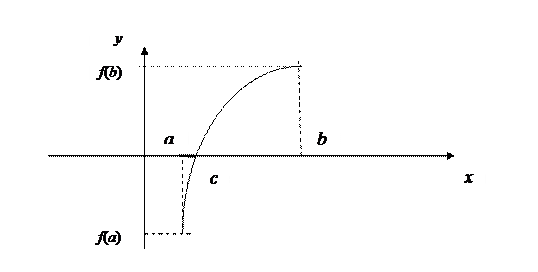
Пусть {x} – множество всех значений х из [a; b] для которых 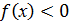 (на рисунке выделено жирной чертой). Это множество не пустое (ему например принадлежит точка а) и ограничено сверху (например, числом х = b). Но тогда существует число, которое будет больше чем любое х из {x} и меньше чем любая из верхних границ. Обозначим это число через с. Заметим, что с Î [a; b]. Убедимся, что
(на рисунке выделено жирной чертой). Это множество не пустое (ему например принадлежит точка а) и ограничено сверху (например, числом х = b). Но тогда существует число, которое будет больше чем любое х из {x} и меньше чем любая из верхних границ. Обозначим это число через с. Заметим, что с Î [a; b]. Убедимся, что 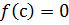 . Если бы это было не так, то по теореме 1 существовала бы окрестность точки с, в пределах которой, функция
. Если бы это было не так, то по теореме 1 существовала бы окрестность точки с, в пределах которой, функция 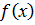 имела бы определенный знак. Но это невозможно, так как существует хотя бы одна точка меньше
имела бы определенный знак. Но это невозможно, так как существует хотя бы одна точка меньше 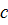 , в которой
, в которой 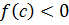 по выбору точки с и существует точка больше c, в которой
по выбору точки с и существует точка больше c, в которой 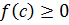 , что означает, что
, что означает, что 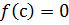
Теорема доказана.
Теорема 3. (Вейерштрасса)
Непрерывная на отрезке [a; b] функция ограничена на нем.
(без доказательства).
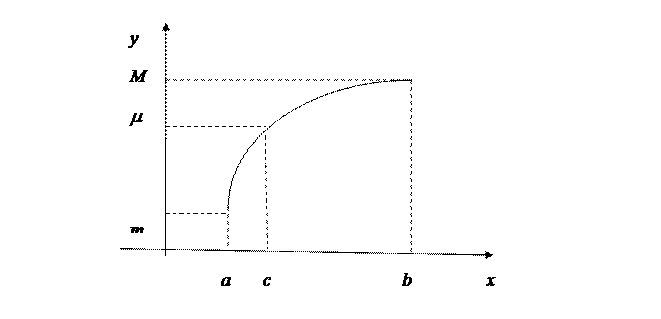
Теорема 4. Если функция 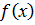 непрерывна на отрезке [a; b], то на нем она принимает наибольшее М =
непрерывна на отрезке [a; b], то на нем она принимает наибольшее М = 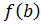 , наименьшее т =
, наименьшее т = 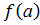 , а также все промежуточные значения m, такие что для произвольного m, где т < m < М существует хотя бы одна точка с Î [a; b], что m =
, а также все промежуточные значения m, такие что для произвольного m, где т < m < М существует хотя бы одна точка с Î [a; b], что m = 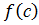 .
. 
(без доказательства).
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|