Непрерывность функции. Классификация точек разрыва

Стр 1 из 2Следующая ⇒

Непрерывность функции

Опр 1. Функция f(x) называется непрерывной в точке x₀, если

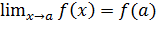(2. 15)

Условие (2. 15) можно переписать в виде:

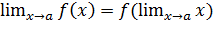
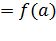то есть возможен предельный переход под знаком функции, если она непрерывна в данной точке.

Опр 2. Функция f(x) называется непрерывной в точке x₀, если

= ,

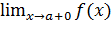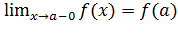т. е. непрерывность функции в точке а равносильна ее непрерывности в этой точке одновременно и справа и слева.

Опр 3. Функция f(x) называется непрерывной в точке x₀, если из того что Dх®0 следует что D f(x) ®0.

Опр. Функция, непрерывная в каждой точке промежутка [a, b], называется непрерывной в [a, b]. Непрерывная функция изображается сплошной кривой.

Классификация точек разрыва

Опр. Если в равенстве

= ,

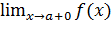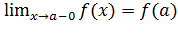нарушено хоть одно условие, то говорят, что при x = a функция f(x) имеет разрыв.

Рассмотрим функцию y = 1/x. Областью определения этой функции является множество R, кроме x = 0. Точка x = 0 является предельной точкой множества D(f), поскольку в любой ее окрестности, т. е. в любом открытом интервале, содержащем точку 0, есть точки из D(f), но она сама не принадлежит этому множеству. Значение f(а)= f(0) не определено, поэтому в точке а = 0 функция имеет разрыв.

1. Если 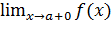существует конечен и не равен 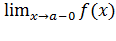, то говорят, что функция f(x) в точке а имеет разрыв первого рода, или скачок.

2. Если 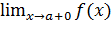существует конечен и равен 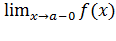, но функция 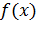в точке а не определена, то говорят, что функция f(x) в точке а имеет устранимый разрыв

3. Если 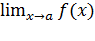равен ¥ или не существует, то говорят, что в точке а функция имеет разрыв второго рода.

Например, функция y = ctg x при x® +0 имеет предел, равный +¥, значит, в точке x=0 она имеет разрыв второго рода.

Утверждение. Все элементарные функции являются непрерывными.

Покажем что степенная функция f(x) = х² является непрерывной. Рассмотрим приращение функции

- =

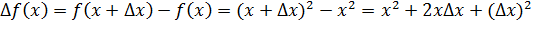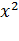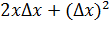= ® 0 + 0 = 0 при Dх®0. Тогда из определения непрерывной функции - степенная функция непрерывна.

Покажем что логарифмическая функция f(x) =lnx является непрерывной. Рассмотрим приращение функции

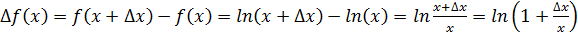® ln1=0 при Dх®0. Тогда из определения непрерывной функции - логарифмическая функция непрерывна.

12 Следующая ⇒