Область применения медианы. Особенности медианы. Медиана

Медиана.. Решение задач

Был проведен опрос среди покупателей с целью выяснить их типичный возраст. По результатам опроса было установлено, что: 25 покупателей имеют возраст до 20 лет; 32 покупателя – 20-40 лет; 18 покупателей – 40-60 лет; 15 покупателей – свыше 60 лет. Найдем медиану.

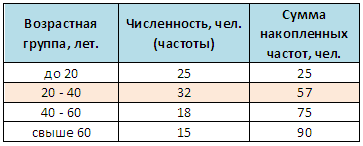
Сначала находим медианный интервал. Для этого вычисляем сумму частот: 25 + 32 + 18 + 15 = 90. Половина этой суммы – 45. Это соответствует возрастной группе 20-40 лет (т. к. полученная полусумма частот – 45, и накопленная частота 1-й группы меньше ее, а 3-ей – больше). Тогда нижняя граница медианного интервала – 20 (лет), а величина медианного интервала – 20 (40 лет за вычетом 20). Сумма частот интервалов предшествующих медианному интервалу – 25. Число значений в медианном интервале – 32 (количество покупателей в возрасте 20-40 лет).

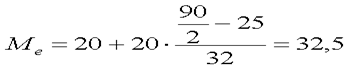
Медиана - 32, 5, следовательно средний возраст покупателя – 33 года.

Область применения медианы

При вычислении типичного признака неоднородных рядов, имеющих « выбросы » - значения во много раз отличающиеся от других значений ряда.

Особенности медианы

· Медиана обладает высокой робастностью, то есть нечувствительностью к неоднородностям и ошибкам выборки.

· Сумма разностей между членами ряда выборки и медианой меньше, чем сумма этих разностей с любой другой величиной. В том числе с арифметическим средним.

Медиана

В статистических исследованиях довольно широко применяются средние величины. Их нахождение позволяет выявить типичное значение признака исследуемой совокупности. Например, типичный уровень доходов покупателей или возраст большинства клиентов компании. При этом вычисление, к примеру, среднего арифметического не всегда уместно. Представим такую ситуацию: мы опросили 10 человек на предмет их уровня доходов. У 9-х доходы оказались примерно одинаковыми и составили 10 тыс. руб. Что касается 10-ого опрошенного, то оказалось, что его доход равняется 410 тыс. руб. в месяц. Если мы вычислим простое среднее арифметическое, то типичный доход будет равняться 50 тыс. руб.! Но это явно не так. В таких ситуациях более объективную и правдоподобную картину дает вычисление моды или медианы, которые относятся к структурным средним показателям.

12 Следующая ⇒