Передаточной функцией системы (звена) W(p) называется отношение изображения по Лапласу выходной величины к изображению по Лапласу входной величины при нулевых начальных условиях.

Лекция 4. Передаточные функции систем автоматического управления

Работу любой САУ можно описать с помощью дифференциального уравнения. Оно является линейным уравнением и определяет линейную модель системы:

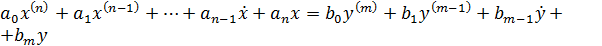(3. 4)

Отметим, что использовать линейную модель для исследования системы можно только при малых отклонениях переменных и поэтому часто говорят, что результаты исследований, полученных при использовании линейной модели справедливы только в малом.

Сложность решения дифференциальных уравнений высокого порядка без применения вычислительной техники и невозможность на основании численных решений создать общие методы анализа и синтеза систем привели к широкому использованию методов, связанных с применением математического аппарата преобразований Лапласа и Фурье. Эти методы и составили сущность так называемой классической теории автоматического управления.

Необходимо отметить, что существуют нелинейные функции, которые невозможно линеаризовать по методу малого отклонения и, в этих случаях, используют специальные методы, разработанные для исследования нелинейных систем.

Понятие передаточной функции системы является основополагающим в классической теории автоматического управления, к изучению основ которой мы и приступаем. Определение передаточной функции связано с преобразование Лапласа и поэтому вначале приведем некоторые основные сведения из этого преобразования.

При использовании преобразования Лапласа некоторой функции времени x(t) ставится в однозначное соответствие функция X(p), где p – оператор Лапласа. Функция времени x(t) называется оригиналом, а функция X(p) ее изображением. Изображение и оригинал связаны соотношением

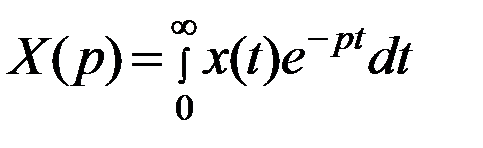
Приведем некоторые теоремы преобразования Лапласа, которые будут использованы при изложении курса.

1. Теорема линейности. Для любых действительных или комплексных

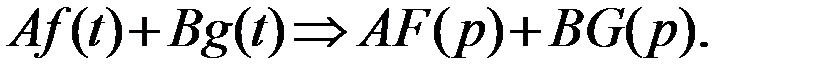
Знак Þ означает соответствие изображения оригиналу.

2. Теорема запаздывания. Для любого постоянного t > 0

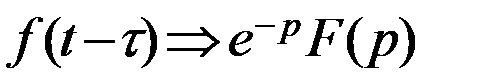
3. Теорема дифференцирования оригинала. Если 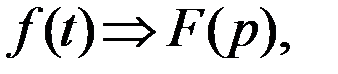то

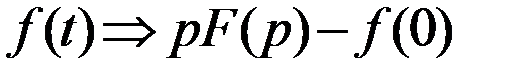
Применив эту теорему к производным высших порядков, получим

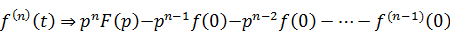(4. 1)

При нулевых начальных условиях выражение (4. 1) упрощается:

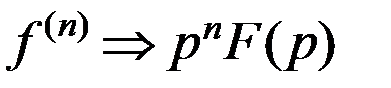
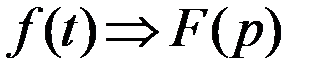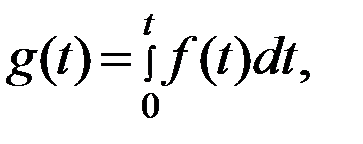4. Теорема интегрирования оригинала. Если и то:

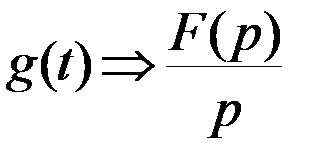
5. Теорема о начальном значении оригинала.

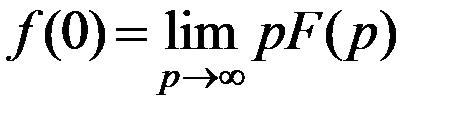
6. Теорема о конечном значении оригинала.

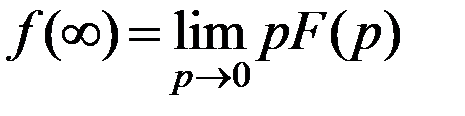
Перейдем к определению передаточной функции. Пусть система или какое-либо звено ее описываются дифференциальным уравнением вида (3. 4). Полагая начальные условия нулевыми, перейдем в этом уравнении к изображениям по Лапласу. В соответствии с теоремой 3 получим

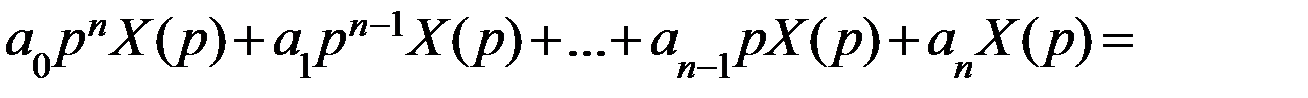
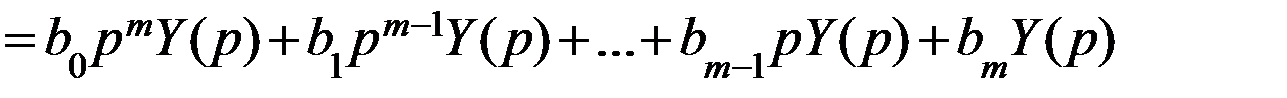Вынесем в полученном выражении за скобки изображения переменной и входного воздействия и сделаем обозначения

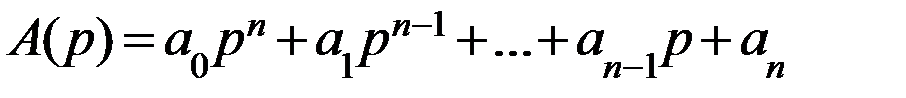
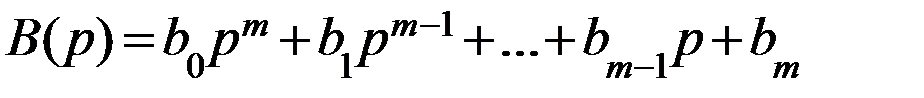
С учетом этих обозначений исходное дифференциальное уравнение в изображениях по Лапласу получит вид:

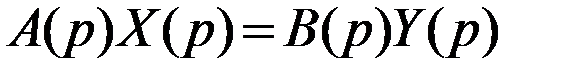
Определим теперь зависимость выходной величины от входного воздействия:

Передаточной функцией системы (звена) W(p) называется отношение изображения по Лапласу выходной величины к изображению по Лапласу входной величины при нулевых начальных условиях.

Требование нулевых начальных условий не вносит принципиальных трудностей. В случае x(0)⁽^k⁾¹ 0, при переходе к изображениям используют теорему 3, переносят члены, соответствующие начальным условиям в правую часть уравнения и считают их возмущающими воздействиями, относительно которых получают передаточные функции.

Будем полагать, что все элементы в схеме замкнутой САУ (рис. 4. 1) описываются уравнениями вида (3. 4). Некоторым исключением в данном случае является уравнение объекта управления, в правую часть которого необходимо добавить оператор 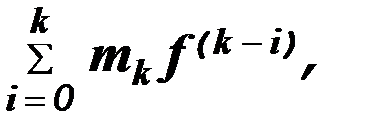определяющий возмущающее воздействие. В соответствии с принципом суперпозии, справедливым только для линейных систем, уравнение объекта управления в изображениях по Лапласу при нулевых начальных условиях запишется в виде

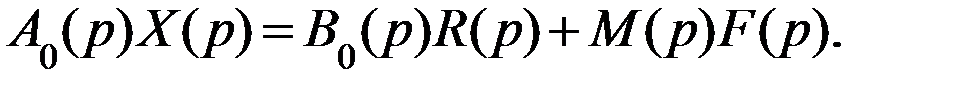
В этом выражении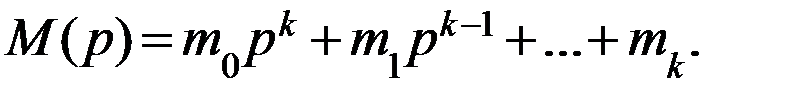

Тогда можно записать

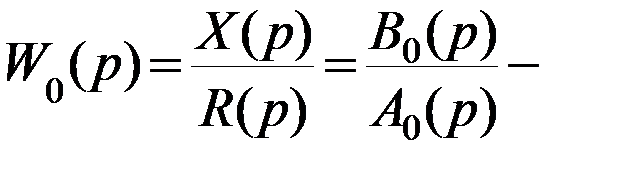передаточная функция объекта управления по регулирующему воздействию.

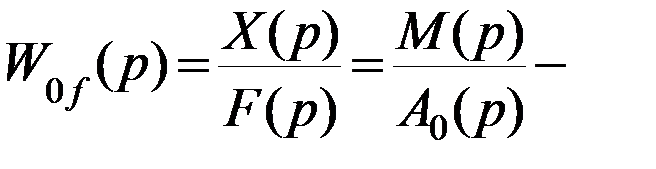передаточная функция объекта управления по возмущению. Аналогично для других элементов схемы запишем

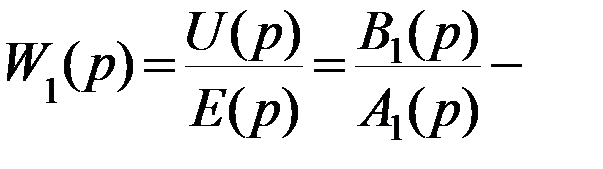передаточная функция логико-вычислительной подсистемы;

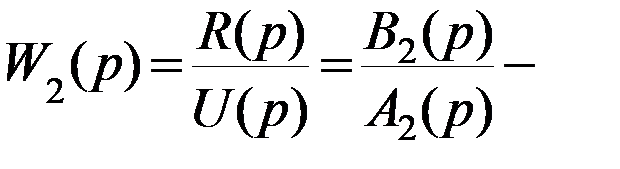передаточная функция исполнительной подсистемы;

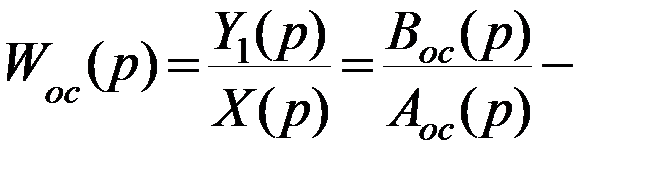передаточная функция цепи обратной связи (информационно-измерительной подсистемы).

X_f(p)

F(p)

W_of(p)

Теперь схему замкнутой САУ можно изобразить, так как показано на рис. 4. 1.

Y(p)

E(p)

W₁(p)

U(p)

W₂(p)

R(p)

W₀(p)

X₁(p)

X(p)

W_ос(p)

Y₁(p)

Рис. 4. 1. Структурная схема САУ.

поменять G(p) на Y(p)

Схема системы автоматического управления, изображенная в виде соединения передаточных функций составляющих ее звеньев, называется структурной схемой. На основании полученной схемы и выражений передаточных функций составим систему уравнений:

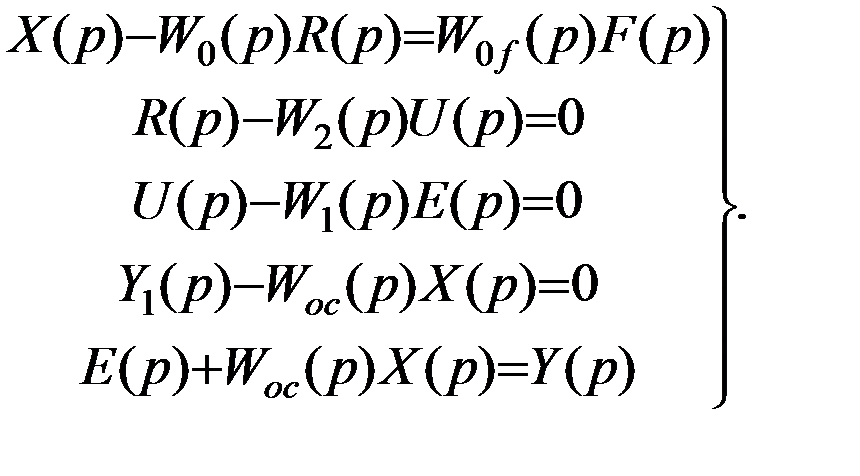(4. 2)

Так как звенья с передаточными функциями W₁(p), W₂(p), W₀(p) входят в прямую цепь регулирования, то передаточная функция W_п(p)=W₁(p)W₂(p)W₀(p)

называется передаточной функцией прямой цепи. Тогда

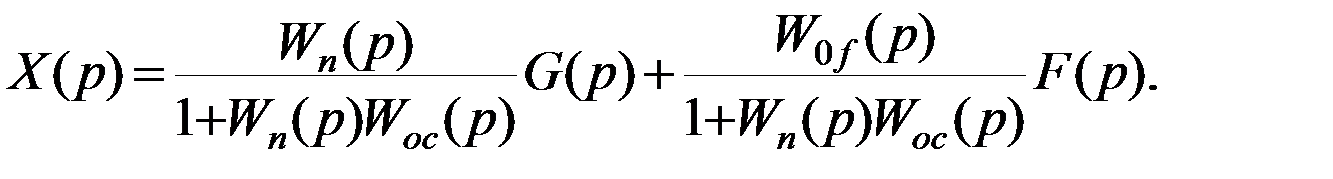(4. 3)

12 Следующая ⇒